
- •Оглавление
- •Часть 1 4
- •Элементы линейной алгебры
- •1.2. Матрицы и операции над ними
- •1.3. Вычисление обратной матрицы
- •1.4. Решение матричных уравнений
- •1.5. Вычисление ранга матрицы
- •1.6. Правило Крамера
- •1.7. Метод полного исключения неизвестных Жордана-Гаусса
- •1.8. Однородные системы линейных уравнений
- •1.9. Действия над векторами
- •1.10. Линейная зависимость и независимость векторов
- •1.11. Базис системы векторов. Переход от одного базиса к другому
- •1.12. Квадратичные формы
- •1.13. Линейные операторы
1.13. Линейные операторы
Определение.
Оператором
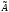 ,
отображающим векторное пространство
,
отображающим векторное пространство
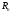 в векторное пространство
в векторное пространство
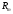 ,
называется функция, которая каждому
вектору
,
называется функция, которая каждому
вектору
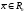 ставит в соответствие единственный
вектор
ставит в соответствие единственный
вектор
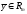 ,
что символически записывается в виде
,
что символически записывается в виде
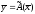 .
Вектор
.
Вектор
 называется образом вектора
называется образом вектора
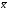 при отображении
при отображении
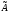 , а вектор
, а вектор
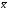 – прообразом вектора
– прообразом вектора
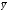 .
.
Оператор
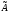 называется линейным, если:
называется линейным, если:
1.
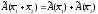 для любых
для любых
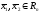
(свойство аддитивности оператора).
2.
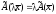 для любого
для любого
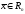 и любого числа
и любого числа
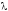
(свойство однородности оператора).
Пусть задан линейный
оператор
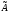 , который отображает вектор
, который отображает вектор
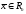 в вектор
в вектор
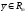 .
.
Связь между
координатами векторов
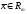 и
и
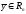 выражается матричным уравнением:
выражается матричным уравнением:
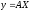 ,
,
где А – матрица
линейного оператора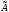 .
.
 ,
,
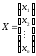 ,
,
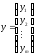 .
.
Если пространства
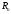 и
и
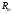 совпадают, то оператор
совпадают, то оператор
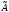 отображает пространство
отображает пространство
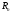 в себя. В этом случае матрицей оператора
в себя. В этом случае матрицей оператора
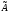 является квадратная матрица
является квадратная матрица
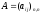 .
.
Определение.
Ненулевой вектор
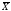 называется собственным вектором
линейного оператора
называется собственным вектором
линейного оператора
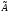 ,
если
,
если
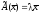 .
.
Число
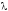 называется собственным значением
(характеристическим числом) оператора
называется собственным значением
(характеристическим числом) оператора
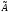 .
.
Собственные векторы
линейного оператора
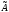 являются ненулевыми решениями матричного
уравнения
являются ненулевыми решениями матричного
уравнения
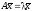
или
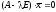 (1.13.1)
(1.13.1)
где
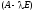 характеристическая матрица.
характеристическая матрица.
Решение уравнения (1.13.1) сводится к решению однородной системы n линейных уравнений, которая имеет ненулевые решения тогда и только тогда, когда определитель системы равен нулю, т.е. когда выполняется условие
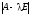 =0 (1.13.2)
=0 (1.13.2)
Уравнение
(5.2) называется характеристическим
уравнением матрицы
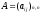 .
.
Характеристическое
уравнение (1.13.2) имеет n
не обязательно различных корней
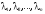 .
Сумма корней равна следу матрицы А, т.е.
.
Сумма корней равна следу матрицы А, т.е.
 ,
а произведение равно определителю
матрицы А:
,
а произведение равно определителю
матрицы А:
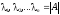 .
.
Пример. Найти
собственные значения и собственные
векторы линейного оператора
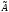 , заданного матрицей
, заданного матрицей
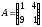 .
.
Решение: Составим характеристическую матрицу:
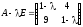 .
.
Вычислим
характеристические числа
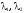 – собственные значения линейного
оператора
– собственные значения линейного
оператора
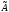 :
:
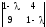 =0
=0
или
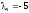 ,
,
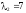 .
.
Находим собственный
вектор
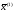 ,
соответствующий собственному значению
,
соответствующий собственному значению
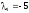 .
Для этого решим матричное уравнение:
.
Для этого решим матричное уравнение:
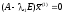
или
 ·
·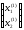 =
= ,
откуда находим
,
откуда находим
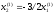
Положив
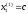 ,
получим
,
получим
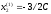 ,
где С постоянная, отличная от нуля.
,
где С постоянная, отличная от нуля.
В частности, при
С=2 получим собственный вектор
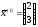 .
.
При
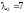 получим матричное уравнение:
получим матричное уравнение:
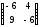 ·
·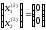 ,
,
откуда
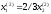 или
или
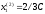 ,
,
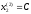 .
.
Собственный вектор
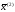 при С=3 имеет вид:
при С=3 имеет вид:
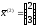 .
.
Таким образом,
собственные векторы линейного оператора
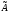 имеют вид:
имеют вид:
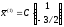 ;
;
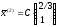 .
.
Упражнения.
Найти собственные
значения и собственные векторы линейного
оператора
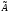 ,
заданного матрицей (в некотором базисе):
,
заданного матрицей (в некотором базисе):
1.13.1.
 1.13.2.
1.13.2.
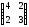 1.13.3.
1.13.3.
 1.13.4.
1.13.4.
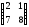
1.13.5.
 1.13.6.
1.13.6.
 1.13.7.
1.13.7.
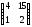 1.13.8.
1.13.8.

1.13.9.
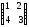 1.13.10.
1.13.10.
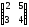 1.13.11.
1.13.11.
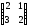 1.13.12.
1.13.12.
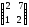
1.13.13.
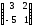 1.13.14.
1.13.14.
 1.13.15.
1.13.15.
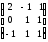
1.13.16.
 1.13.17.
1.13.17.
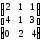 1.13.18.
1.13.18.

1.13.19.
 1.13.20.
1.13.20.

