9. Технология программирования вложенных циклов

В предыдущих главах рассмотрены варианты простых (одинарных) циклов и смешанных вычислительных процессов, объединяющих один внешний цикл с внутренним линейным и/или ветвящимся процессами. Это позволяет перейти к рассмотрению более сложных структур с вложенными циклами.

Вычисления с вложенными циклами – процесс, в котором хотя бы один цикл расположен внутри другого.

Вложенный (внутренний) – цикл, расположенный внутри другого.

Внешний (наружный) – цикл, внутри которого располагаются другие циклы.

При многократном вложении циклов некоторые из них могут быть внутренними и внешними одновременно.

Разновидности вложенных циклов определяет форма их расположения (рис. 9.1).

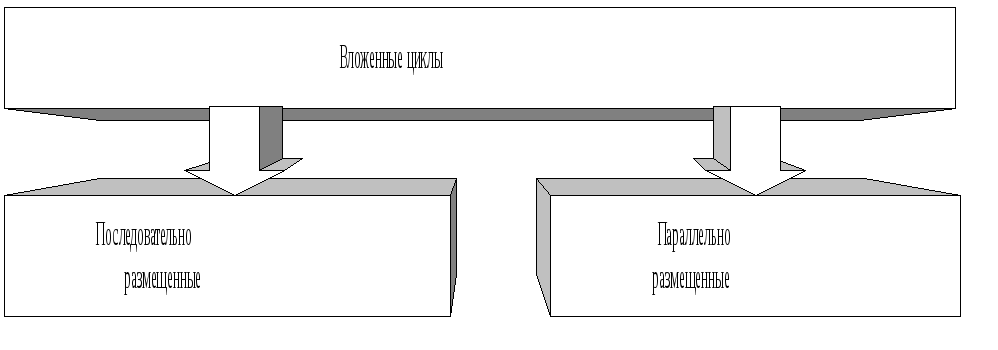
Рис. 9.1. Разновидности вложенных циклов

Последовательно размещенные (вложенные) циклы – структура, в которой каждый следующий цикл полностью расположен внутри предыдущего (другого);

Параллельно размещенные (вложенные) циклы – структура, во внешнем цикле которой два или более цикла расположены один под другим.

Графические изображения различных вариантов вложений (сплошные линии – тело цикла, штриховые – передача управления) представлены следующими структурами:

• Последовательно вложенные циклы

Цикл 1 является внешним по отношению к 2 и 3. Цикл 2 является внешним по отношению к 3 и внутренним по отношению к 1. Цикл 3 является вложенным по отношению к 1 и 2.

Минимальное количество последовательно вложенных циклов – один. Максимальное – не ограничено.

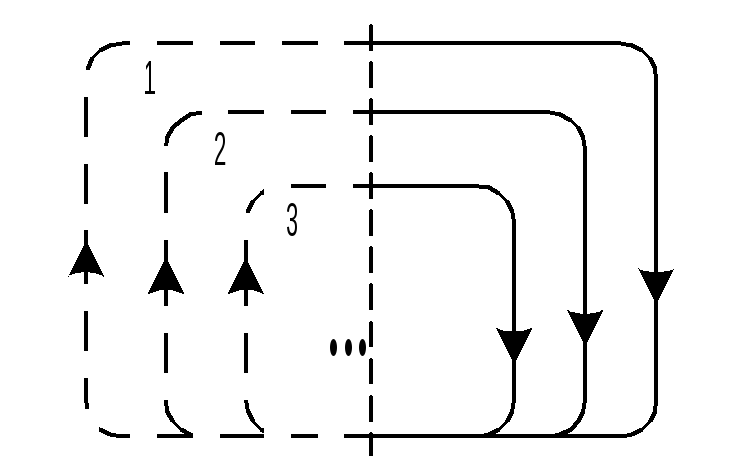
• Последовательно вложенные циклы с общим основанием

Разновидностью последовательно вложенных циклов являются циклы с общим основанием.

Этот вид вложенных циклов является единственным, где осуществляется соединение циклов в какой-либо точке (по основанию тела цикла).

Ц

икл 1 является внешним по отношению к 2 и 3. Цикл 2 является внешним по отношению к 3 и внутренним по отношению к 1. Цикл 3 является вложенным по отношению к 1 и 2. Общее основание – выход из цикла.

• Параллельно вложенные циклы

Цикл 1 является внешним по отношению к 2 и 3. Циклы 2 и 3 являются параллельно вложенными в 1.

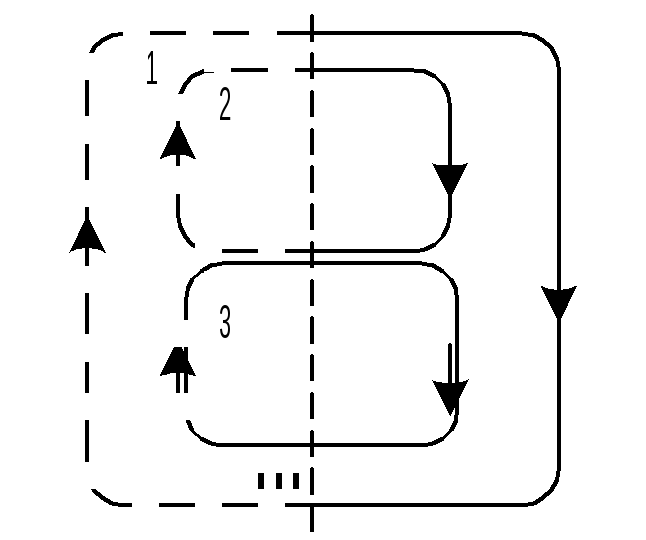
Минимальное количество параллельно вложенных циклов – два. Максимальное – не ограничено.

• Смешанный (универсальный) вариант.

Ц

икл 1 является внешним по отношению к 2 и 3. Циклы 2 и 3 являются параллельно вложенными в 1.

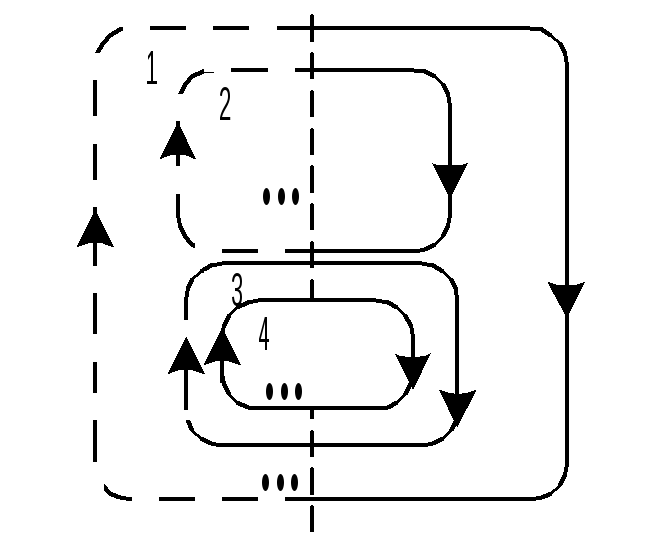
Цикл 4 – последовательно вложен в цикл 3 и параллельно в цикл 2.

Максимальное количество вложений – не ограничено.

Правила работы с вложенными циклами:

• пересечение циклов запрещается;

• каждый из них составляется и выполняется как обычный цикл;

• передача управления из вложенного цикла в наружный разрешается, так как для вложенного цикла такая передача является искусственным выходом из цикла, а для внешнего – обычным ветвлением внутри него;

• передача управления из внешнего цикла во внутренний разрешается только естественным путём – через начало (заголовок) цикла. Другие варианты запрещаются ввиду нарушения выполнения внутреннего цикла;

• из вложенного цикла разрешается передача управления вне внешнего цикла с условием возврата в точку выхода. Такая передача используется при работе с подпрограммами.

Предмашинная подготовка вычислительных процессов с вложенными циклами детализировано рассмотрена ниже на конкретных примерах.

1. Последовательно вложенные циклы

Типовое использование последовательно вложенных циклов – обработка многомерных массивов (задач, в которых они используются) и преобразования одномерных массивов (сортировка элементов).

Варианты использования (функционального назначения) вложенных циклов представлены на рис. 9.2.

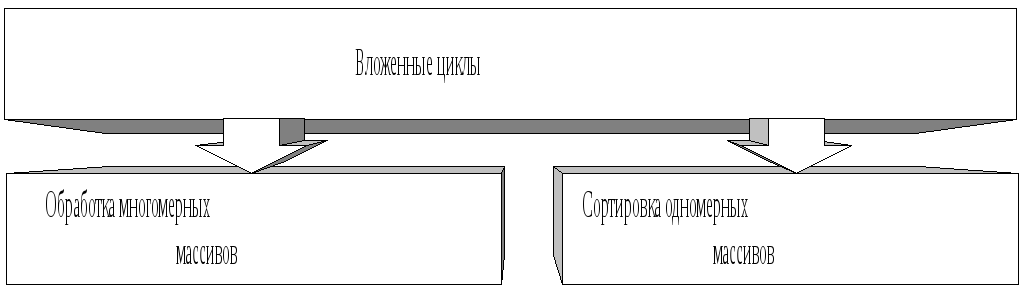
Рис. 9.2. Функциональное назначение вложенных циклов

1. Обработка элементов многомерных массивов

Рассмотрим обработку многомерных массивов на конкретной задаче (9.1) о расчете элементов двумерного массива.

1. Постановка задачи

Имеется двумерный массив X размером (mn). Рассчитать аналогичный ему массив Y(mn), каждый элемент которого равен частному от деления соответствующего элемента массива X на два.

2. Формирование математической модели

Исходные данные

m – размер, определяющий число строк матрицы X ();

n – размер, определяющий число столбцов матрицы X ().

Модель матрицы X(mn):

x11	x12	...	x1j	...	x1n
x21	x22	...	x2j	...	x2n
...	...	...	...	...	...
xi1	xi2	...	xij	...	xin
...	...	...	...	...	...
xm1	xm2	...	xmj	...	xmn

1im – диапазон изменения номера i строки;

1jn – диапазон изменения номера j столбца.

Расчётные зависимости

Вычисление текущего элемента искомой матрицы Y:

, для всех 1im и 1jn

М

1im

1jn

одель матрицы Y(mn):

y11	y12	...	y1j	...	y1n
y21	y22	...	y2j	...	y2n
...	...	...	...	...	...
yi1	yi2	...	yij	...	yin
...	...	...	...	...	...
ym1	ym2	...	ymj	...	ymn