Выбор метода решения

Анализ полученной математической формулировки позволяет сделать выводы:

• решение задачи требует многократного вычисления подоходного налога Нал_i, однозначно зависящего от величины зарплаты З_i, следовательно, процесс является циклическим, а параметр цикла есть З_i;

• диапазон изменения параметра цикла задан зависимостью З_н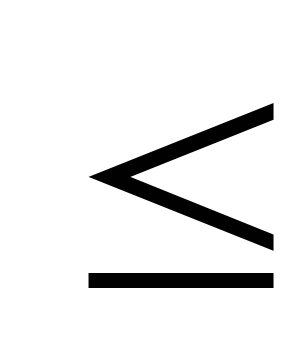З_iЗ_к, что позволяет сформулировать начальное значение параметра З_i=З_н и условие повторения цикла З_iЗ_к, невыполнение которого приводит к выходу из него;

• закон изменения параметра цикла имеет вид З_i = З_i-1 + З, т.е. является аналитическим;

• количество повторений цикла N можно определить до начала счёта по стандартной формуле.

Следовательно, в качестве метода решения необходимо использовать циклический процесс арифметического типа с аналитическим изменением параметра.

Составление алгоритма

Возможны две методики составления алгоритма циклического процесса арифметического типа:

Вариант 1 а) Сформировать первое текущее значение параметра (аргумента) цикла (xi); б) проверить полученное значение (xi) на соответствие диапазону счета. Если условие не выполняется – выйти из цикла. Если выполняется – сохранить естественный порядок вычислений – перейти к пункту в); в) вычислить текущее значение искомой функции ( yi = f ( xi ) );	Вариант 2 а) Сформировать первое текущее значение параметра (аргумента) цикла (xi); б) рассчитать текущее значение искомой функции ( yi = f ( xi ) ); в) зафиксировать текущие значения аргумента и функции (xi , yi ); г) сформировать новое текущее значение параметра цикла (xi=xi-1+x);
г) зафиксировать текущие значения аргумента и функции (xi , yi ); д) сформировать новое текущее значение параметра цикла (xi=xi-1+x); е) перейти к пункту б).	д) проверить полученное значение (xi) на соответствие диапазону счета. Если условие повторения цикла выполняется – нарушить естественный порядок выполнения – перейти к пункту б), в противном случае – выйти из цикла.

Анализ представленных методик позволяет сделать выводы:

• первый вариант выполняет формальное требование проверки всех текущих значений параметра цикла (x_i) на соответствие диапазону счета;

• второй вариант предполагает ненужность проверки первого значения x_i, т.к. для него условие повторения цикла должно выполняться автоматически;

• по месту проведения проверки параметра цикла (x_i) на соответствие диапазону изменения первый вариант формирует цикл с предусловием, второй – с постусловием.

Алгоритмы, реализующие для рассматриваемой задачи каждую из методик, представлены схемами на рис. 5.4 и 5.5.

• Внимание! Формирование тела цикла в любой из схем происходит при выполнении условия повторения цикла. При этом в цикле с предусловием сохраняется естественный порядок выполнения блоков, а в цикле с постусловием – нарушается.

Алгоритмы содержат все необходимые элементы циклического процесса:

• вход в цикл (блоки 4);

• тело цикла (блоки 6, 7, 8);

• выход из цикла (блок 5 рис. 5.4; блок 9 рис. 5.5).

Расчёт количества повторений N может быть осуществлён вне тела цикла в любом месте алгоритма.

Схема алгоритма цикла с предусловием (рис. 5.4) может стать более компактной, если функции трех блоков (4, 5, 8) передать одному блоку «начало цикла». Модифицированный алгоритм представлен схемой на рис. 5.6. Он реализует стандартную структуру цикла с параметром. При этом блок «начало цикла» формирует начальное значение параметра цикла и проверяет его на соответствие диапазону изменения.

Если условие выполняется – сохраняет естественный порядок вычислений (предписывает однократное выполнение тела цикла), а затем вычисляет новое значение параметра и предписывает его очередную проверку на соответствие заданному диапазону.

При невыполнении проверяемого условия – управление передается блоку, следующему за телом цикла.

• Внимание! Алгоритмы цикла с параметром совмещают два стандартных элемента циклического процесса – вход в цикл и выход из него (блок 4). Тело цикла образуют блоки 5 и 6.

Представленные схемы выполнены в стандартном (унифицированном) изображении. Они наглядны, но недостаточно информативны, т.к. не позволяют понять логику переходов при проверке условий.

Этого недостатка лишены развёрнутые изображения алгоритмов (рис. 5.7).