
Пример решения задачи 1
Однородная
прямоугольная плита весом Р закреплена
сферическим шарниром в точке А,
цилиндрическим – в точке Д и невесомым
шарнирным стержнем СС1, расположенным
в плоскости, параллельной ZХ. К плите
приложена сила
![]() в плоскости YZ и пара сил в плоскости XY
с моментом M. Точка приложения силы,
направление силы, линейные размеры
плиты показаны на схеме. Определить
реакции связей в точках A,C,Д.
в плоскости YZ и пара сил в плоскости XY
с моментом M. Точка приложения силы,
направление силы, линейные размеры
плиты показаны на схеме. Определить
реакции связей в точках A,C,Д.
Дано: P=2 кН, F=10 кН, M=3 кНм, α=30º, а=0,5 м.
Определить: реакции в точках А,С,Д.
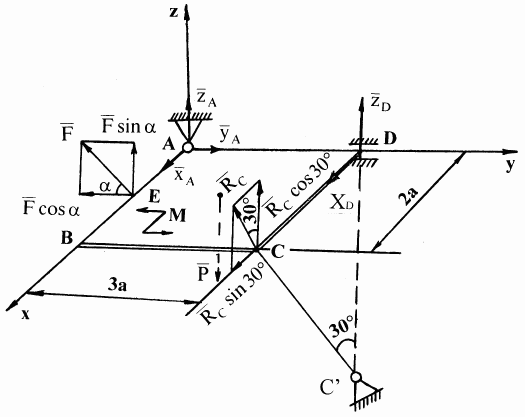
Рис. 1
Решение
-
Изобразим схему плиты с опорами и действующие на нее силы в соответствии с условием задачи (Рис. 1).
-
Для определения реакций в точках А, С, Д рассмотрим равновесие плиты АВСД.
-
Покажем на схеме реакции связей. Реакцию неподвижного сферического шарнира представим в виде трех составляющих
 ,
,
 ,
,
 ,
реакцию цилиндрического шарнира –
двумя составляющими
,
реакцию цилиндрического шарнира –
двумя составляющими
 ,
реакцию
,
реакцию
 невесомого стержня направим по линии
стержня.
невесомого стержня направим по линии
стержня.
Разложим
силы
![]() и
и
![]() на составляющие, параллельные осям.
на составляющие, параллельные осям.
![]() =
=![]() cosα
+
cosα
+![]() sinα;
sinα;
![]() =
=
![]() cos30º+
cos30º+
![]() sin30º
sin30º
-
Составим шесть уравнений равновесия полученной системы сил.
-
Σ Fкх =0; XA + Rcsin30º+ XД=0
-
Σ Fky=0; YA- Fcosα α=0
-
Σ Fkz=0; ZA+ Fsinα+ Rccos30º+ZД- P=0
-
Σ Mx(Fk)=0; Rccos30º*3a+ ZД*3a- P*1,5a=0
-
Σ My(Fk)=0; -Fsinα*a- Rccos30º*2a+ P*a=0
-
Σ Mz(Fk)=0; -Fcosα*a- Rcsin30º*3а-XД*3а+М=0
Решим полученную систему уравнений.
Из уравнения 2:
YА=Fcosα=10*cos30º=8,66 кН
Из уравнения 5:
Rс=![]()
Из уравнения 6:

Из уравнения 1:
XA = -Rcsin30º-X2 = -1,73*sin30º+1,75=0,9 кН
Из уравнения 4:
ZД
=
![]()
Из уравнения 3:
ZA= -Fsinα-Rccos30º-ZД+P= -10*sin30º-1,73cos30º+2= -1,5 кН
Ответ: XA=0,9 кН, YA=8,66 кН, ZA=1,5 кН
XД= -1,75 кН, ZД=0 кН, Rc= -1,73 кН
Знаки минус
указывают, что реакции
![]() ,
,
![]() ,
,
![]() направлены противоположно принятому
на схеме.
направлены противоположно принятому
на схеме.
П ример
2. Стержень
АВ в
точке С
опирается
на стержень СD
(рис. 2).
ример
2. Стержень
АВ в
точке С
опирается
на стержень СD
(рис. 2).
Определить реакции в точках А, С, Е и D, если Р = 200 Н, F = 400 H,АС =СВ =в =3 м, СЕ = ЕК = КD = a = 2 м, М=300 Нм.
Решение.

 На
составную конструкцию действуют активные
силы Р и
Q,
пара сил с моментом
М, а также
подлежащие определению шесть реакций
ХА,
УА,
ХD,
YD,
NE,
и
NC.,
при этом NC
= - NC1.
На
составную конструкцию действуют активные
силы Р и
Q,
пара сил с моментом
М, а также
подлежащие определению шесть реакций
ХА,
УА,
ХD,
YD,
NE,
и
NC.,
при этом NC
= - NC1.
Покажем на чертеже направления всех реакций как внешних, так и внутренних, и составим уравнения равновесия для всей конструкции (рис. 3).
![]()
![]() .
.
![]()
![]() .
(1)
.
(1)


В эти три уравнения входят пять неизвестных реакций ХА, УА, ХD, YD, NE.
Сделаем чертежи и рассмотрим равновесие каждого тела.
Выбираем оси координат и составляем уравнения равновесия для стержня АВ (рис.4).
![]()
![]() (2)
(2)
![]()
В систему уравнений (2) входят три неизвестные реакции: ХА, УА и N C , и мы можем однозначно определить их значения. Выбираем оси координат и составляем уравнения равновесия для стержня СD (рис.5).
![]() .
.
![]() (3)
(3)
![]() .
.
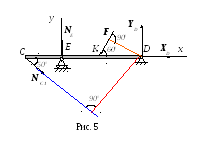
Из этих уравнений определяются последние три неизвестные реакции ХD, YD, NE .
Таким образом, для конструкции, состоящей из двух твердых тел, можно составить девять уравнений равновесия. Для данной задачи оптимальными являются уравнения (2) и (3), из которых находятся все внешние и внутренние реакции.
С1 на расстоянии: СС1 = 0, 4 см.
