
- •Кафедра математики
- •Введение.
- •Механика Основные формулы.
- •Силы, рассматриваемые в механике.
- •Задачи.
- •Молекулярная физика и термодинамика. Основные формулы.
- •Задачи.
- •Электростатика. Постоянный ток. Основные формулы.
- •Задачи.
- •Электромагнитизм. Основные формулы.
- •Задачи.
- •Оптика. Основные формулы.
- •Задачи.
- •Физика атома и атомного ядра. Основы квантовой механики. Основные формулы.
- •Атомное ядро. Радиоактивность.
- •Задачи.
- •О приближенных вычислениях.
- •Справочные материалы.
- •Астрономические величины.
- •Приставки для обозначения кратных и дольных единиц.
- •Плотность жидкостей,ρ10–3, кг/м3.
- •Поверхностное натяжение жидкостей при 200с, Дж/м2.
- •Плотность, модуль Юнга, коэффициент линейного расширения.
- •Масса нейтральных атомов, а.Е.М.
- •Периоды полураспада изотопов.
- •Греческий алфавит.
- •Литература. Основная литература и пособия
- •Дополнительная литература
Механика Основные формулы.
Кинематическое
уравнение движения материальной точки
(центра массы твёрдого тела) вдоль оси
![]() :
:
![]()
где
![]() –некоторая функция времени.
–некоторая функция времени.
Проекция средней
скорости на ось
![]() :
:
![]()
Средняя скорость движения:
![]() =
=![]()
где
![]()
путь, пройденный точкой за интервал
времени
путь, пройденный точкой за интервал
времени
![]() .
.
Путь
![]() ,
в отличие от разности координат
,
в отличие от разности координат
![]() ,
не может убывать и принимать отрицательные
значения, т.е.
,
не может убывать и принимать отрицательные
значения, т.е.
![]() .
.
Проекция мгновенной
скорости на ось
![]() :
:
![]()
Проекция среднего
ускорения на ось
![]() :
:
![]() =
=![]()
Проекция мгновенного
ускорения на ось
![]() :
:
![]()
Кинематическое
уравнение движения материальной точки
по окружности (![]() ):
):
![]() ,
,
Модуль угловой скорости:
![]()
Модуль углового ускорения:
![]()
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
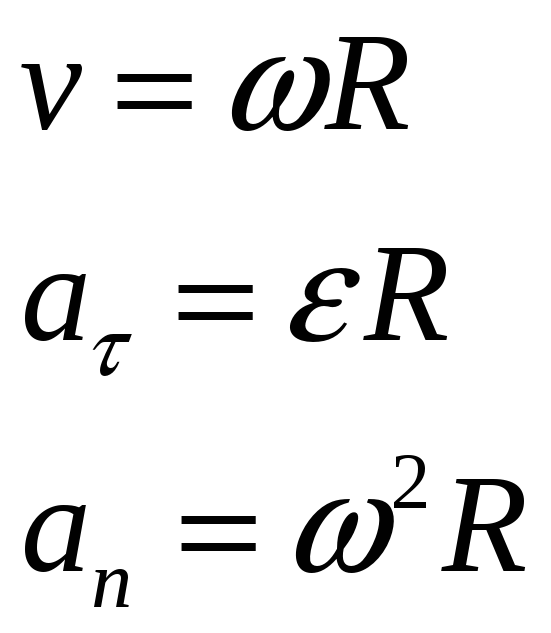
где
![]()
модуль линейной скорости;
модуль линейной скорости;
![]() и
и
![]()
модули тангенциального и нормального
ускорений;
модули тангенциального и нормального
ускорений;
![]() –
модуль угловой скорости;
–
модуль угловой скорости;
![]()
модуль углового ускорения; R
радиус окружности.
модуль углового ускорения; R
радиус окружности.
Модуль полного ускорения:
![]() или
или
![]()
Угол между полным
a
и нормальным a![]() ускорениями:
ускорениями:
![]()
Кинематическое уравнение гармонических колебаний материальной точки:
![]()
где
![]()
смещение; A–
амплитуда колебаний;
смещение; A–
амплитуда колебаний;
![]()
угловая или циклическая частота;
угловая или циклическая частота;
![]() начальная
фаза.
начальная
фаза.
Скорость и ускорение материальной точки, совершающей гармонические колебания:
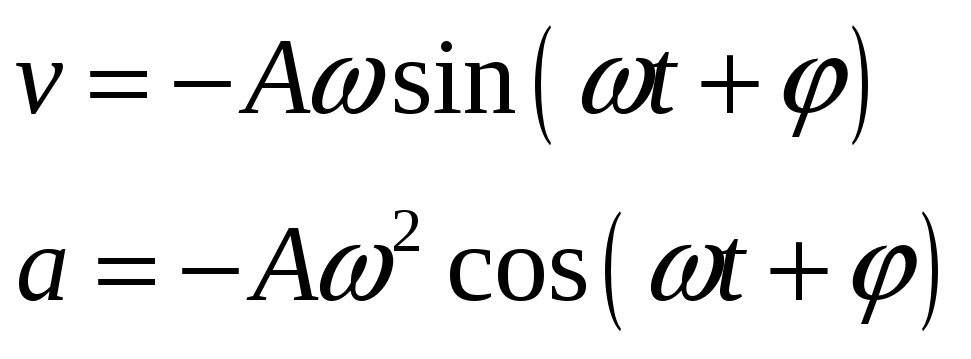
Сложение гармонических колебаний одного направления и одинаковой частоты:
амплитуда
результирующего колебания
![]()
начальная фаза результирующего колебания
![]()
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях:
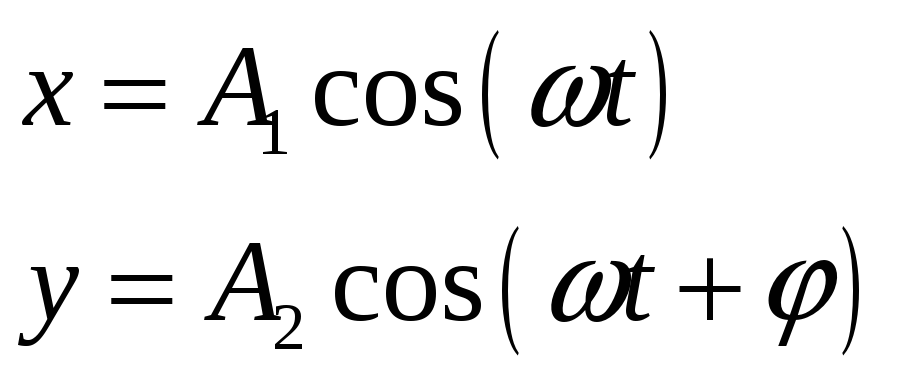
a)
![]() если разность фаз
если разность фаз
![]() ;
;
б)
![]() если разность фаз
если разность фаз
![]() ;
;
в)
![]() если разность фаз
если разность фаз
![]()
Уравнение плоской бегущей волны:
![]()
где
![]()
смещение любой из точек среды с координатой
смещение любой из точек среды с координатой
![]() в момент
в момент
![]() ;
;
![]()
скорость распространения колебаний в
среде,
скорость распространения колебаний в
среде,
![]() – волновое число.
– волновое число.
Связь разности
фаз
![]() колебаний с расстоянием
колебаний с расстоянием
![]() между точками среды, отсчитанным в
направлении распространения колебаний:
между точками среды, отсчитанным в
направлении распространения колебаний:
![]()
где
![]()
длина волны.
длина волны.
Импульс материальной
точки массой m,
движущейся со скоростью
![]() ,
,
![]()
Второй закон Ньютона:
![]()
где
![]()
результирующая сила, действующая на
материальную точку.
результирующая сила, действующая на
материальную точку.
Силы, рассматриваемые в механике.
сила упругости
![]()
где
![]()
коэффициент упругости ( в случае пружины
– жёсткости);
коэффициент упругости ( в случае пружины
– жёсткости);
![]() абсолютная
деформация;
абсолютная
деформация;
сила тяжести
![]() ;
;
сила гравитационного взаимодействия
![]()
где
![]()
гравитационная постоянная;
гравитационная постоянная;
![]() и
и
![]()
массы взаимодействующих тел;
массы взаимодействующих тел;
![]()
расстояние между телами. Силу можно
выразить через напряженность
гравитационного поля
расстояние между телами. Силу можно
выразить через напряженность
гравитационного поля
![]() :
:
![]()
(тела
рассматриваются как материальные
точки). В случае гравитационного
взаимодействия силу можно выразить
также через напряжённость
![]() гравитационного поля.
гравитационного поля.
сила трения (скольжения)
F=![]() ,
,
где
![]()
коэффициент трения; N
сила нормального давления.
коэффициент трения; N
сила нормального давления.
Закон сохранения импульса.
![]() ,
,
или для двух тел
(![]() )
)
![]() ,
,
где
![]() v
v![]() и v
и v![]()
скорости тел в момент времени, принятый
за начальный; u
скорости тел в момент времени, принятый
за начальный; u![]() и u
и u![]()
скорости тех же тел в момент времени,
принятый за конечный.
скорости тех же тел в момент времени,
принятый за конечный.
Кинетическая энергия тела, движущегося поступательно:
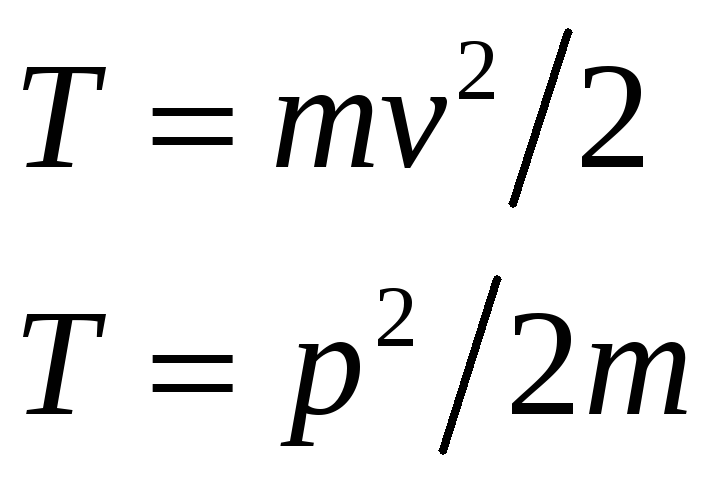
Потенциальная энергия:
упруго деформированной пружины
![]()
где k жёсткость пружины; x абсолютная деформация;
гравитационного взаимодействия
![]() ,
,
где
![]()
гравитационная постоянная; m
гравитационная постоянная; m![]() и m
и m![]()
массы взаимодействующих тел; r
расстояние между ними (тела рассматриваются
как материальные точки);
массы взаимодействующих тел; r
расстояние между ними (тела рассматриваются
как материальные точки);
тела, находящегося в однородном поле силы тяжести,
![]()
где g
ускорение свободного падения; h
высота тела над уровнем, принятым за
нулевой (формула справедлива при условии
![]() ,
где R
радиус Земли).
,
где R
радиус Земли).
Закон сохранения механической энергии
E=T+П=const.
Работа A, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:
ΣA=![]() .
.
Основное уравнение
динамики вращательного движения
относительно неподвижной оси
![]() :
:
![]()
где
![]()
результирующий момент внешних сил
относительно оси
результирующий момент внешних сил
относительно оси
![]() ,
действующих на тело; ε
угловое ускорение;
,
действующих на тело; ε
угловое ускорение;
![]()
момент инерции тела относительно оси
вращения.
момент инерции тела относительно оси
вращения.
Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:
стержня длиной l относительно оси, перпендикулярной стержню
![]()
обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)
![]() ,
,
где R радиус обруча (цилиндра);
диска радиусом R относительно оси, перпендикулярной плоскости диска,
![]() .
.
Проекция на ось
![]() момента импульса тела, вращающегося
относительно неподвижной оси
момента импульса тела, вращающегося
относительно неподвижной оси
![]() :
:
![]()
где
![]()
угловая скорость тела.
угловая скорость тела.
Закон сохранения
момента импульса системы тел, вращающихся
вокруг неподвижной оси
![]() :
:
![]() .
.
Кинетическая
энергия тела, вращающегося вокруг
неподвижной оси
![]() :
:

