Максимум и минимум функций

Точка х0 называется точкой максимума функции у=ƒ(х), если существует такая d -окрестность точки х0, что для всех х≠х0 из этой окрестности выполняется неравенство ƒ(х)<ƒ(х0).

Аналогично определяется точка минимума функции: x0 — точка минимума функции, если $d >0 " х: 0<|x-x0|<d Þ ƒ(х)>ƒ(х0). На рисунке 146 х1 — точка минимума, а точка х2 — точка максимума функции у=ƒ(х).

Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.

Понятие экстремума всегда связано с определенной окрестностью точки из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения. Рассмотрим условия существования экстремума функции.

Теорема 8 (необходимое условие экстремума). Если дифференцируемая функция у=ƒ(х) имеет экстремум в точке х0, то ее производная в этой точке равна нулю: ƒ'(х0)=0.

Пусть, для определенности, x0 — точка максимума. Значит, в окрестности точки х0 выполняется неравенство ƒ(х0)>ƒ(х0+∆х). Но тогда

если ∆х>0, и ∆у/∆х>0, если ∆х<0.

По условию теоремы производная

существует. Переходя к пределу, при ∆х→0, получим ƒ'(x0)≥0, если ∆х<0, и f'(х0)≤0, если ∆х>0. Поэтому ƒ'(х0)=0. Аналогично доказывается утверждение теоремы 25.8, если х0 — точка минимума функции ƒ(х).

Геометрически равенство ƒ'(х0)=0 означает, что в точке экстремума дифференцируемой функции у=ƒ(х) касательная к ее графику параллельна оси Ох (см. рис. 147).

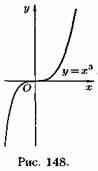
Отметим, что обратная теорема неверна, т. е. если ƒ'(х0)=0, то это не значит, что х0-точка экстремума. Например, для функции у=х3 ее производная у'=3х2 равна нулю при х=0, но х=0 не точка экстремума (см. рис. 148).

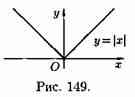
Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция у=׀ х׀ в точке х=0 производной не имеет, но точка х=0 — точка минимума (см. рис. 149).

Таким образом, непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.

Теорема 9(достаточное условие экстремума). Если непрерывная функция у=ƒ(х) дифференцируема в некоторой d -окрестности критической точки х0 и при переходе через нее (слева направо) производная ƒ'(х) меняет знак с плюса на минус, то х0 есть точка максимума; с минуса на плюс, то х0 — точка минимума.

Рассмотрим d -окрестность точки х0. Пусть выполняются условия: ƒ'(х)>0 " xє(х0-d ;х0) и ƒ'(х)<0 " xє(х0;х0+d ). Тогда функция ƒ(х) возрастает на интервале (х0-δ; х0), а на интервале (х0; х0+d ) она убывает. Отсюда следует, что значение ƒ (х) в точке x0 является наибольшим на интервале (х0-δ;х0+δ), т. е. ƒ(х)<ƒ(х0) для всех хє(х0-d ;x0)U(x0;x0+d ). Это и означает, что х0 — точка максимума функции.

Графическая интерпретация доказательства теоремы 9 представлена на рисунке 150.

Аналогично теорема 9 доказывается для случая, когда ƒ'(х)<0 " x є(х0-d ;х0) и ƒ'(х)>0 " xє(х0;х0+d ).

Исследовать функцию на экстремум означает найти все ее экстремумы. Из теорем 8 и 9 вытекает следующее правило исследования функции на экстремум:

1) найти критические точки функции у=ƒ(х);

2) выбрать из них лишь те, которые являются внутренними точками области определения функции;

3) исследовать знак производной ƒ'(х) слева и справа от каждой из выбранных критических точек;

4) в соответствии с теоремой 9 (достаточное условие экстремума) выписать точки экстремума (если они есть) и вычислить значения функции в них.

Теорема 10. Если в точке х0 первая производная функции ƒ(х) равна нулю (ƒ'(х0)=0), а вторая производная в точке х0 существует и отлична от нуля (ƒ"(х0)¹ 0), то при ƒ"(х0)<0 в точке х0 функция имеет максимум и минимум — при ƒ"(х0)>0.

Пусть для определенности ƒ"(х0)>0. Так как

То в достаточно малой окрестности точки х0. Если ∆х<0,

то ƒ'(х0+∆х)<0; если ∆х>0, то ƒ'(х0+∆х)>0.

Таким образом, при переходе через точку x0 первая производная меняет знак с минуса на плюс. Следовательно, по теореме 9, х0 есть точка минимума.

Аналогично доказывается, что если ƒ"(х0)<0, то в точке х0 функция имеет максимум.