
- •Бесконечно большая функция
- •Бесконечно малые функции
- •Теоремы о пределах
- •Признаки существования предела
- •Непрерывность функции в точке
- •Точки разрыва функции и их классификация
- •Определение производной; ее механический и геометрический смысл.
- •Связь между непрерывностью и дифференцируемостью функции
- •Замечания:
- •Производная суммы, разности, произведения и частного функций
- •Производные основных элементарных функций
- •Производная сложной и обратной функций
- •Понятие дифференциала функции
- •Геометрический смысл дифференциала функции
- •Основные теоремы о дифференциалах
- •Некоторые теоремы о дифференцируемых функциях
- •Правила Лопиталя
- •Раскрытие неопределенностей различных видов
- •Возрастание и убывание функций
- •Максимум и минимум функций
- •Наибольшее и наименьшее значения функции на отрезке
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты графика функции
- •Понятие неопределенного интеграла
- •Свойства неопределенного интеграла
- •Метод непосредственного интегрирования
- •30.2. Метод интегрирования подстановкой (заменой переменной)
- •30.3. Метод интегрирования по частям
- •31.2. Интегрирование простейших рациональных дробей
- •31. 3. Интегрирование рациональных дробей
- •Универсальная тригонометрическая подстановка
- •Квадратичные иррациональности
- •33.2. Дробно-линейная подстановка
- •33.3. Тригонометрическая подстановка
- •33.4. Интегралы типа
- •33.5. Интегрирование дифференциального бинома
- •§ 35. Определенный интеграл как предел интегральной суммы
- •Геометрический и физический смысл определенного интеграла
- •Формула Ньютона-Лейбница
- •§ 38. Основные свойства определенного интеграла
- •39.1. Формула Ньютона-Лейбница
- •39.2. Интегрирование подстановкой (заменой переменной)
- •39.3. Интегрирование по частям
- •39.4. Интегрирование четных и нечетных функций в симметричных пределах
- •§ 40. Несобственные интегралы
- •40.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
- •40.2. Интеграл от разрывной функции (несобственный интеграл II рода)
- •§ 41. Геометрические и физические приложения определенного интеграла Додати до моєї бази знань Математика
- •41.1. Схемы применения определенного интеграла
- •41.2. Вычисление площадей плоских фигур
- •41.3. Вычисление длины дуги плоской кривой
- •41.4. Вычисление объема тела
- •41.5. Вычисление площади поверхности вращения
- •41.6. Механические приложения определенного интеграла
40.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл I рода)
Пусть функция ƒ(х) непрерывна на промежутке
[а;+∞). Если существует конечный предел то
его называют несобственным интегралом
первого рода и обозначают
то
его называют несобственным интегралом
первого рода и обозначают

Таким образом, по определению
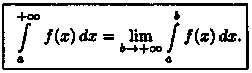
В этом случае говорят, что несобственный
интеграл сходится.
сходится.
Если же указанный предел не существует
или он бесконечен, то говорят, что
интеграл dx расходится.
dx расходится.
Аналогично определяется несобственный интеграл на промежутке (-∞; b]:


Несобственный интеграл с двумя бесконечны ми пределами определяется формулой

где с — произвольное число.
В этом случае интеграл слева сходится
лишь тогда, когда сходятся оба интеграла
справа. Отметим, что если непрерывная
функция ƒ (х) ≥ 0 на промежутке [а; +∞) и
интеграл сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции (см.
рис. 172).
сходится,
то он выражает площадь бесконечно
длинной криволинейной трапеции (см.
рис. 172).
Пример 40.1. Вычислить несобственные интегралы или установить их расходимость:
1)
 2)
2)
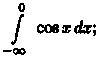 3)
3)

Решение:
1)
 интеграл
сходится;
интеграл
сходится;
2)
 интеграл
расходится, так как при а →-∞ предел
интеграл
расходится, так как при а →-∞ предел![]() не
существует.
не
существует.
3)
 интеграл
расходится.
интеграл
расходится.
В некоторых задачах нет необходимости вычислять интеграл; достаточно лишь знать, сходится ли он или нет.
Приведем без доказательства некоторые признаки сходимости.
Теорема 40.1 (признак сравнения). Если на промежутке [а; +∞) непрерывные функции ƒ(х) и φ(х) удовлетворяют условию 0 ≤ ƒ(х) ≤ φ(х), то из сходимости
интеграла следует
сходимость интеграла
следует
сходимость интеграла а
из расходимости интеграла следует
расходимость интеграла
а
из расходимости интеграла следует
расходимость интеграла
Пример 40.2. Сходится ли интеграл
Решение: При х ≥ 1 имеем![]() Но
интеграл
Но
интеграл
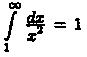 сходится.
Следовательно, интеграл
сходится.
Следовательно, интеграл также
сходится (и его значение меньше 1).
также
сходится (и его значение меньше 1).
Теорема 40.2. Если существует
предел![]() и
φ(х) > 0), то интегралы
и
φ(х) > 0), то интегралы одновременно
оба сходятся или оба расходятся (т. е.
ведут себя одинаково в смысле сходимости).
одновременно
оба сходятся или оба расходятся (т. е.
ведут себя одинаково в смысле сходимости).
Пример 40.3. Исследовать сходимость
интеграла
Решение: Интеграл сходится,
так как интеграл
сходится,
так как интеграл
 сходится
и
сходится
и

40.2. Интеграл от разрывной функции (несобственный интеграл II рода)
Пусть функция ƒ(х) непрерывна на промежутке
[а; b) и имеет бесконечный разрыв при х =
b. Если существует конечный предел то его называют несобственным интегралом
второго рода и обозначают
то его называют несобственным интегралом
второго рода и обозначают

Таким образом,поопределению,

Е сли
предел в правой части существует, то
несобственный интеграл
сли
предел в правой части существует, то
несобственный интеграл
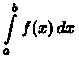 сходится.
Если же указанный предел не существует
или бесконечен,то говорят, что интеграл
сходится.
Если же указанный предел не существует
или бесконечен,то говорят, что интеграл
 расходится.
расходится.
Аналогично, если функция ƒ (х) терпит бесконечный разрыв в точке х = а, то полагают

Если функция ƒ(х) терпит разрыв во внутренней точке с отрезка [а; b], то несобственный интеграл второго рода определяется формулой

В этом случае интеграл слева называют
сходящимся, если оба несобственныхинтеграла,
стоящих справа, сходятся. В случае, когда
ƒ(х) > 0, несобственный интеграл второго
рода
 (разрыв в точке х = b) можно истолковать
геометрически как площадь бесконечно
высокой криволинейной трапеции (см.
рис. 173).
(разрыв в точке х = b) можно истолковать
геометрически как площадь бесконечно
высокой криволинейной трапеции (см.
рис. 173).
Пример 40.4. Вычислить![]()
Решение: При х = 0 функция
![]() терпит бесконечный разрыв;
терпит бесконечный разрыв;

интеграл расходится.
Сформулируем признаки сходимости для несобственных интегралов второго рода.
Теорема 40.3. Пусть на промежутке [а; b) функции ƒ(х) и φ(х) непрерывны, при х = b терпят бесконечный разрыв и удовлетворяют условию 0 ≤ ƒ(х) ≤ φ(x).
Из сходимости интеграла вытекает
сходимость интеграла
вытекает
сходимость интеграла а
из расходимости интеграла
а
из расходимости интеграла вытекает
расходимость интеграла
вытекает
расходимость интеграла
Теорема 40.4. Пусть функции
ƒ(х) и φ(х) непрерывны на промежутке [а;
b) и в точке х = b терпят разрыв. Если
существует предел![]() то
интегралы
то
интегралы одновременно
сходятся или одновременно расходятся.
одновременно
сходятся или одновременно расходятся.
Пример 40.5. Сходится ли интеграл
Решение: Функция![]() имеет
на [0; 1] единственный разрыв в точке х =
0. Рассмотрим функцию
имеет
на [0; 1] единственный разрыв в точке х =
0. Рассмотрим функцию![]() ,
Интеграл
,
Интеграл

расходится. И так как
![]()
то интеграл также
расходится.
также
расходится.
