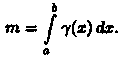Геометрический и физический смысл определенного интеграла

Площадь криволинейной трапеции

Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

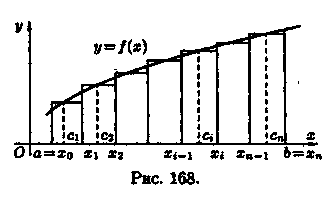
Для этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х0<x1<...<xn) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).

Умножим значением функции ƒ(ci) на длину ∆xi=xi-xi-1 соответствующего частичного отрезка. Произведение ƒ(ci) • ∆xi равно площади прямоугольника с основанием ∆xi и высотой ƒ(ci). Сумма всех таких произведений

равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

С уменьшением всех величин Δхi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что

λ = max∆xi →0:

Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом состоит геометрический смысл определенного интеграла.

Работа переменной силы

Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х—абсцисса движущейся точки М.

Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку

х = b (а < b). Для этого отрезок [а; b] точками а = х0, х1, ..., b = хn (х0 < x1 < ... < хn) разобьем на n частичных отрезков [х0; x1], [x1; x2],..., [xn-1; xn]. Сила, действующая на отрезке [xi-1; xi], меняется от точки к точке. Но если длина отрезка Δхi = хi-xi-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = ci Î [xi-1; xi]. Поэтому работа, совершенная этой силой на отрезке [xi-1;xi], равна произведению F(ci)•Δхi (Как работа постоянной силы F(ci) на участке [xi-1; xi].)

Приближенное значение работы А силы F на всем отрезке [а; b] есть

Это приближенное равенство тем точнее, чем меньше длина Δхi Поэтому за точное значение работы А принимается предел суммы (36.1) при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].

В этом состоит физический смысл определенного интеграла.

Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t=а до t=b, равен определенному интегралу от скорости v(t):

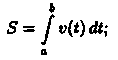
масса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от плотности g(х):