31.2. Интегрирование простейших рациональных дробей

Найдем интегралы от проcтeйшиx рациональных дробей.

1. (формула (2) таблицы интегралов);

2. (формула (1));

3. Рассмотрим интеграл

Выделив в знаменателе полный квадрат, получим:

причем . Сделаем подстановку Тогда , dx=dt. Положим . Следовательно, используя формулы (2) и (15) таблицы интегралов, получаем

т. е., возвращаясь к переменной х,

Пример 31. 5. Найти

Решение: х^2+2х+10=(х+1)^2+9. Сделаем подстановку х+1=t. Тогда х=t-1, dx=dt и

4. Вычисление интеграла вида

5. Данный интеграл подстановкой сводится к сумме двух интегралов:

Первый интеграл легко вычисляется:

Вычислим второй интеграл:

К последнему интегралу применим интегрирование по частям. Положим

тогда

Подставляя найденный интеграл в равенство (31. 8), получаем

т. е.

Полученная формула дает возможность найти интеграл Jк для любого натурального числа k>1.

Пример 31. 6. Найти интеграл

Решение: Здесь а=1, к=3. Так как

то

31. 3. Интегрирование рациональных дробей

Рассмотренный в пунктах 1-3 материал позволяет сформулировать общее правило интегрирования рациональных дробей.

1. Если дpобь неправильна, то представить ее в виде суммы многочлена и правильной дpоби (см. пункт 2);

2. Разложив знаменатель правильной рациональной дpоби на множители, представить ее в виде суммы простейших рациональных дробей;

3. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример 31. 7. Найти интеграл

Решение: Под знаком интеграла неправильная дробь; выделим ее целую часть путем деления числителя на знаменатель:

Пoлyчаем:

Разложим правильную рациональную дробь на простейшие дроби:

4х^3+4х^2+4х+4 ≡ Ах(х^2+2х+2)+В(х^2+2х+2)+(Сх+D)x^2, т. е.

4х^3+4^2+4х+4 ≡ (А+С)х^3+(2А+В+D)x^2+(2А+2В)х+2В.

Отсюда следует, что

Находим: В=2, А=О, С=4, D=2. Стало быть,

и

Интегрируем полученное равенство:

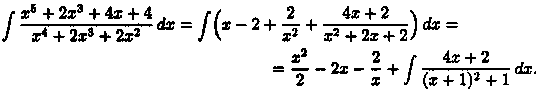
Обозначим х+1=t, тогда х=t-1 и dx=dt. Таким обpaзoм,

Следовательно,

Отметим, что любая рациональная функция интегрируется в элементарных функциях.

Универсальная тригонометрическая подстановка

Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать R(sin x;cos x), где R - знак рациональной функции.

Вычисление неопределенных интегралов типасводится к вычислению интегралов от

рaциoнaльнoй фyнкции подстановкой, которая называется универсальной.

Действительно,

Поэтому

где R1(t) - рациональная функция от t. Обычно этот способ весьма громоздкий, зато он всегда приводит к результату.

На практике применяют и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной фyнкции. В частнocти, удобны следующие правила:

1) если функция R(sinx;cos x) нечетна относительно sinx, т.е. R(— sinx;cos x)=— R(sin x;cos x), то подстановка cosx=t рационализирует интеграл;

2) если функция R(sinx;cos x) нечетна относительно cosx, т.е. R(sinx; - cosx)=—R(sinx;cosx), то делается подстановка sinx=t;

3) если функция R(sin x; cos x) четна относительно sinx и cosx R(— sin x; - cos x)=R(sin x; cos x), то интеграл рационализируется подстановкой tgx=t. Такая же подстановка применяется, если интеграл имеет вид

Пример 32.1. Найти интеграл

Решение: Cделаем универсальную подстановку Тогда dx=

, , . Следовательно,

Пример 32.2. Найти интеграл

Решение: Так как

то полагаем tg x=t. Отсюда

Поэтому

32.2. Интегралы типа ∫(sinх)^m•(cosx)^n dx

Для нахождения таких интегралов используются следующие приемы:

1) подстановка sinx=t, если n - целое положительное нечетное число;

2) подстановка cosx=t, если m - целое положительное нечетное число;

3) формулы понижения порядка: (cosx)^2=1/2(1+cos2x), (sinx)^2 =1/2(1-cos 2x), sinx-cosx =1/2 sin2x, если тип - целые неотрицательные четные числа;

4) подстановка tg х=t, если m+n - есть четное отрицательное целое число.

Пример 32.3. Найти интеграл

Решение: Применим подстановку sinx=t. Тогда х=arcsint dx

Пример 32.4. Найти интеграл

Решение:

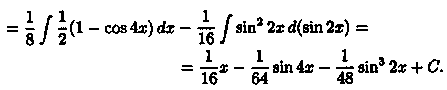
Пример 32.5. Найти интеграл

Решение: Здесь m+n =-4. Обозначим tg x=t. Тогда х=arctg t,

и

Использование тригонометрических преобразований

Интегралы типа вычисляются с помощью известных формул тригонометрии:

Пример 32.6. Найти интеграл

Решение: