Выбор модуля и числа зубьев

Модуль и числа зубьев и не входят в выражения (3.17) и (3.18) для расчёта и непосредственно. Они входят в них лишь косвенно, т.е. величина контактных напряжений не зависит от модуля и числа зубьев в отдельности, а определяется только их произведением. По условиям контактной прочности при данных или модуль передачи может быть сколь угодно малым, лишь бы соблюдалось равенство:

и

Поэтому величину модуля выбирают на основе опыта эксплуатации передач, а затем проверяют на изгиб. При этом руководствуются следующими соображениями:

• мелкомодульные колёса с большим числом зубьев предпочтительны по условиям плавности хода передачи, меньшему расходу материала (уменьшается наружный диаметр);

• крупномодульные колёса дольше противостоят износу, менее чувствительны к нагрузкам.

; при .

при

Расчёт прочности зубьев по напряжениям изгиба

При расчете зубьев на прочность по напряжениям изгиба вводят следующие допущения:

• Нагрузка передаётся одной парой зубьев и приложена к вершине зуба.

• Зуб рассматриваем как консольную балку, для которой справедлива гипотеза плоских сечений.

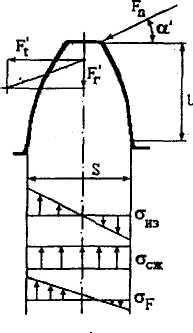
Рис.3.5

Действующие силы:

• сила нормального давления в точке контакта зубьев (3.5);

• окружная сила

- угол направления нормальной силы. Угол несколько больше угла :

Перенесём силу на ось симметрии зуба и разложим её на составляющие:

I

;

Напряжение изгиба в опасном сечении, расположенном вблизи хорды основной окружности:

(3.19)

где - момент сопротивления;

- площадь;

- ширина зубчатого венца;

- теоретический коэффициент концентрации напряжений.

За расчётные напряжения принимают растягивающие напряжения, так как в большинстве случаев усталостные трещины возникают здесь. Размерные величины и неудобные для расчета. Так как зубья различного модуля геометрически подобны, то величины и выражают через безразмерные величины:

и .

где - модуль зубьев.

Подставим в выражение (3.19) для расчёта напряжений изгиба в опасном сечении значения всех составляющих. Получим:

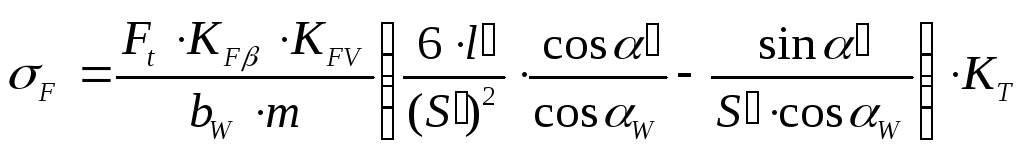, (3.20)

где - коэффициент неравномерности нагрузки;

- коэффициент динамической нагрузки при расчёте зубьев на изгиб.

Введём обозначение:

- удельная расчетная окружная сила;

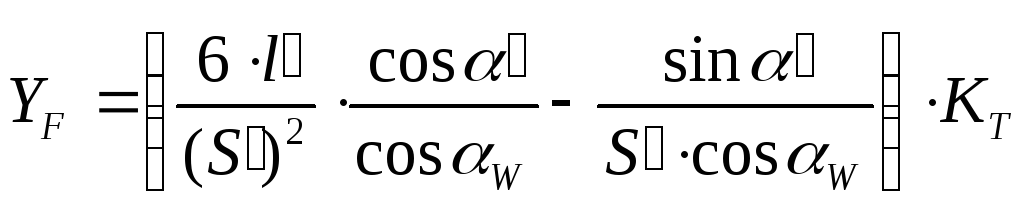- коэффициент формы зуба.

Величина зависит от числа зубьев и коэффициента смещения исходного контура и определяется по специальным графикам. С учётом этих обозначений условие прочности на изгиб запишется:

(3.21)

Полученная формула (3.21) является основной для проверочного расчёта прямозубой передачи. Для проектных расчётов эту формулу разрешают относительно модуля. Выражая окружную силу через вращающий момент на шестерне и принимая из условия (3.21), найдем

(3.22)

где - коэффициент. Можно принять для прямозубой передачи .

Значения модуля округляют до ближайшего значения из ряда модулей по ГОСТ 9563-60 и по принятому значению модуля находят размеры колес. Ширина шестерни в прямозубой передаче выполняется несколько больше номинальной ширины для компенсации неточностей установки в осевом направлении.

Из формулы (3.22) видно, что модуль и, как следствие, габариты передачи могут быть уменьшены за счет повышения прочности материала колес, а также путем уменьшения концентрации нагрузки вдоль зуба (уменьшения и увеличения ).

Колеса с малым модулем зацепления предпочтительны по условиям плавности и экономичности, однако крупномодульные колеса менее чувствительны к перегрузкам, неоднородности материала и погрешности изготовления в меньшей степени влияют на прочность зубьев. Поэтому для силовых передач значения принимать не следует.

9