Сходимость метода конечных элементов

Рассматривается дифференциальное уравнение

, (1.31)

с граничными условиями

. (1.32)

Коэффициент a(t) считается непрерывно дифференцируемым на [0, 1], а коэффициенты c(t) и y(t) – непрерывными на [0, 1]. Пусть на отрезке [0, 1]

. (1.33)

Обобщенным решением задачи ( 1 .31) – ( 1 .32) называется функция , удовлетворяющая тождеству ( 1 .23) для всех , где в данном случае

,

.

Иными словами, тождество ( 1 .23) получается в результате скалярного умножения в уравнения ( 1 .31) на произвольную функцию и интегрирования по частям. Это позволяет понизить требования гладкости к функции x(t), одновременно повысив требования дифференцируемости функции v(t). В качестве координатной системы в выбирается система функций (рис. 1 .7)

Рис. 1.7. Вид функции _i координатной системы

Для задачи ( 1 .31) – ( 1 .32) показано [18], что ее обобщенное решение в действительности принадлежит . Там же получена оценка, показывающая, что для всякой функции при

,

где P_m – проектор в H¹(0, 1) на подпространство кусочно-линейных функций, натянутое на . Таким образом, из оценки теоремы 1.1 следует сходимость галеркинских аппроксимаций x_m к точному решению задачи.

Контрольные вопросы и задания

• Сформулируйте идею метода взвешенных невязок

• Сформулируйте требования к пробным функциям, используемым в методе взвешенных невязок, и обоснуйте их необходимость

• Сформулируйте требования к взвешивающим функциям, используемым в методе взвешенных невязок, и обоснуйте их необходимость

• Какой смысл вкладывается в название слабая формулировка задачи?

• Что представляет собой слабое решение задачи?

• Какой смысл вкладывается в название обратная формулировка задачи?

• При каком условии метод взвешивающих невязок приводит к поиску решения дифференциальной задачи только на границе?

• Приведите классификацию методы взвешенных невязок.

• При каких условиях метод моментов оказывается частным случаем метода взвешенных невязок?

• При каких условиях метод Галеркина оказывается частным случаем метода взвешенных невязок?

• При каких условиях метод наименьших квадратов оказывается частным случаем метода взвешенных невязок?

• При каких условиях метод коллокаций оказывается частным случаем метода взвешенных невязок?

• При каких условиях метод подобластей оказывается частным случаем метода взвешенных невязок?

• При каких условиях метод конечных разностей оказывается частным случаем метода взвешенных невязок?

2. Аппроксимация функций

В классе методов, объединенных названием методы взвешенных невязок, применяются специальные процедуры аппроксимации функций, основанные на разложении в ряды по системам кусочно-гладких функций.

Функции одной переменной

Первоначально рассматриваются способы и алгоритмы аппроксимации функций с помощью кусочно-постоянных, кусочно-линейных и кусочно-квадратичных функций.

Кусочно-постоянные функции

Для определенности рассмотрим аппроксимацию функции на отрезке G = [0, 1]. Представим этот отрезок объединением , где , . На каждом из этих интервалов (рис. 2 .0) определим кусочно-постоянные пробные функции

Рис. 2.0. Пробные кусочно-постоянные функции

Представим заданную функцию f(x) в виде разложения

, (2.0)

причем в рассматриваемом случае, очевидно, m = 4. Взвесим погрешность

представления функции в области G, используя в качестве взвешивающих те же самые функции _k,

.

Потребуем равенства нулю всех взвешенных на рассматриваемом отрезке погрешностей,

. (2.1)

Эти равенства представляют собой систему четырех линейных алгебраических уравнений относительно четырех искомых коэффициентов разложения ( 2 .0). В соответствии с выражением ( 2 .1) подсчитаем значения интегралов

, ,

.

Аналогично вычисляются остальные интегралы. Подстановка их значений в выражение ( 2 .1) приводит к системе четырех линейных алгебраических уравнений

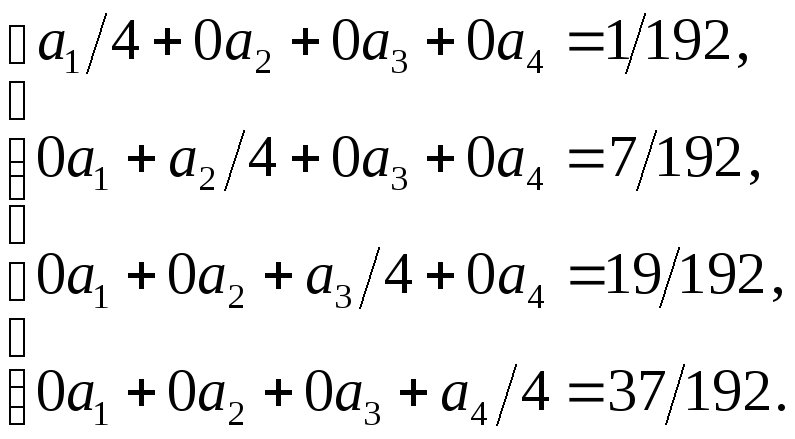(2.2)

Искомые коэффициенты разложения равны

Аппроксимация функции на отрезке [0, 1] с помощью представления ( 2 .0) показана на рис. 2 .1.

Рис. 2.1. Аппроксимация зависимости кусочно-постоянными пробными функциями