Уравнение нестационарной теплопроводности

Рассматривается одномерное уравнение нестационарной теплопроводности для тонкого однородного стержня с теплоизолированной боковой поверхностью

(3.18)

с граничными

(3.19)

и начальными условиями

. (3.20)

Здесь дополнительно введены обозначения: c – удельная теплоемкость,  – плотность материала. Как и ранее, для упрощения W, c,  и  считаются постоянными величинами.

Весь отрезок длиной L разбивается на ряд равных отрезков длиной h каждый. Решение задачи на произвольном отрезке [x_i, x_j] строится с помощью разделения переменных в виде

.

Например, для кусочно-линейной аппроксимации это выражение представляется в форме

. (3.21)

Невязка уравнения ( 3 .18), получаемая на решении ( 3 .21), взвешивается с весовыми функциями _i и _j,

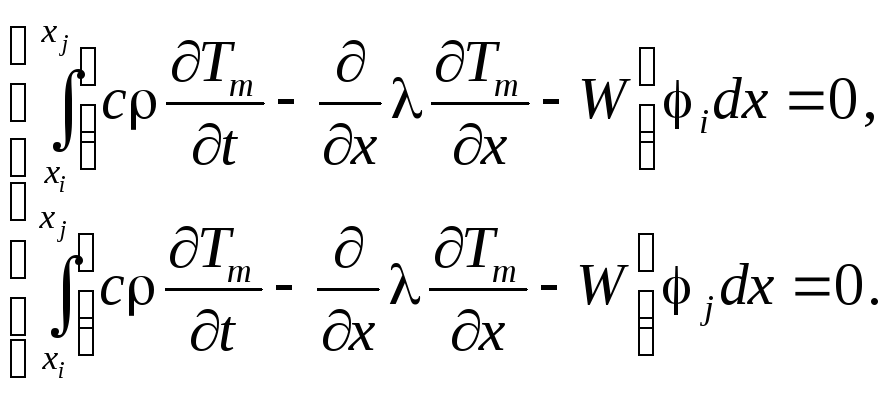(3.22)

Выполняются преобразования первого из этих уравнений:

,

,

.

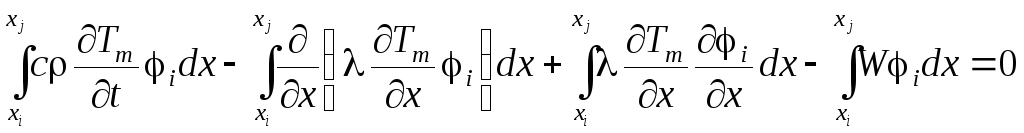Учитывая, как и ранее, что

,

последнее соотношение приводится к виду

.

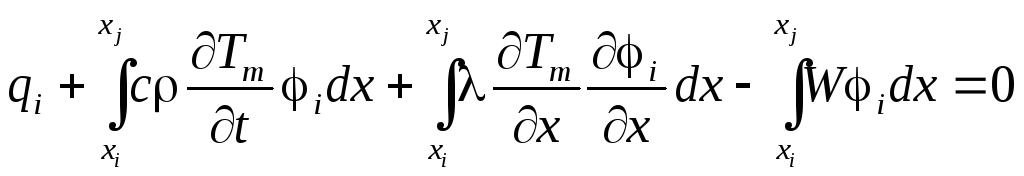Подстановка разложения ( 3 .21) приводит к выражению

.

Аналогичные преобразования второго уравнения системы ( 3 .22) приводят к соотношению

.

В сравнении с системой уравнений ( 3 .5) и ( 3 .6) последние выражения содержат дополнительные слагаемые, которые определяются с учетом вида функций и :

,

,

.

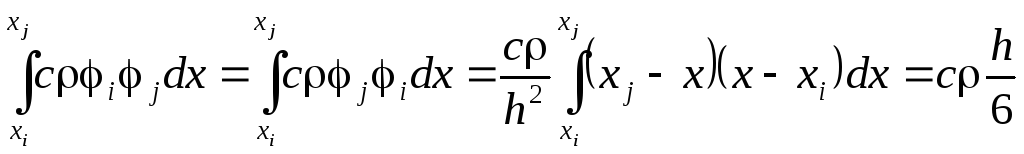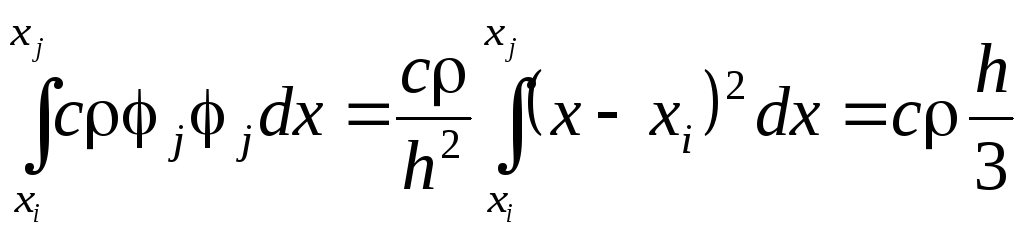Теперь система обыкновенных дифференциальных уравнений относительно узловых значений температуры T_i(t) и T_j(t) имеет вид:

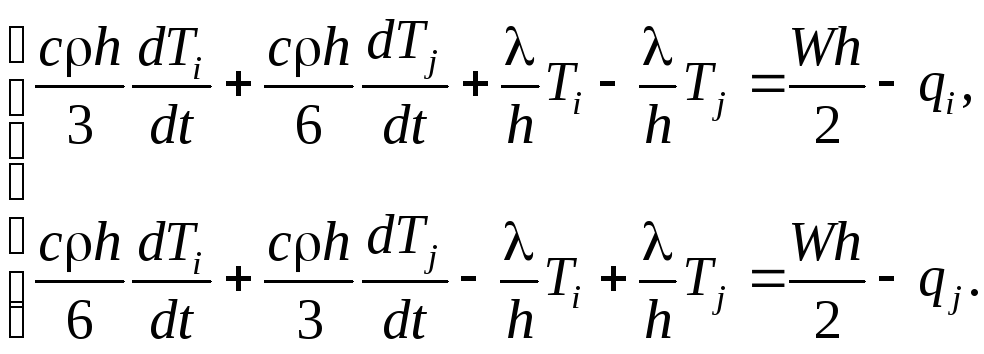
Удобно полученную систему уравнений представить в матричной форме

. (3.23)

Здесь использованы матричные обозначения:

, , , .

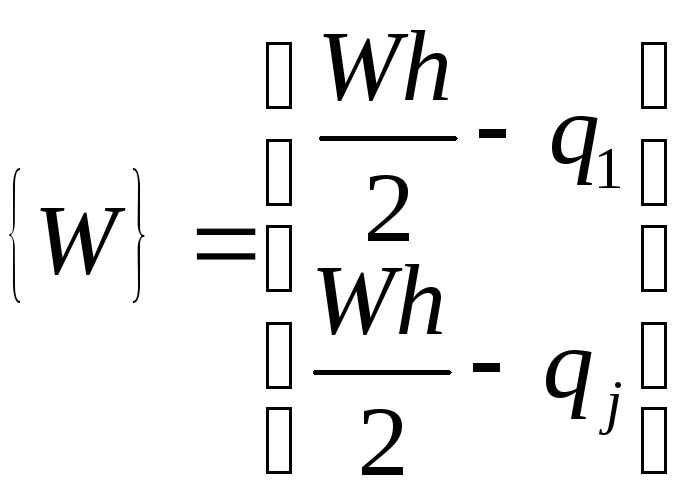Для интегрирования системы обыкновенных дифференциальных уравнений ( 3 .23) могут быть использованы схемы

• явная

,

• неявная

,

• Крэнка-Николсона

.

Последняя разностная схема в виде системы линейных алгебраических уравнений

наиболее часто используется при решении прикладных задач нестационарной теплопроводности. Использование процедуры ансамблирования для всех конечных элементов, аппроксимирующих рассматриваемый стержень, позволяет исключить внутренние неизвестные тепловые потоки q_i и q_j.

Контрольные вопросы и задания

• Объясните, в чем заключается причина некорректности постановки задачи ( 3 .0) – ( 3 .1).

• Опишите порядок построения разрешающих соотношений метода взвешенных невязок для стационарного уравнения теплопроводности.

• Покажите, что системы уравнений ( 3 .15), ( 3 .16) и ( 3 .17) имеют определители, равные нулю.

• Поясните, почему при использовании иерархической системы функций в системах уравнений ( 3 .15), ( 3 .16) и ( 3 .17) отсутствуют длины h конечных элементов?

• С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения стационарной теплопроводности с использованием кусочно-линейной аппроксимации решения.

• С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения стационарной теплопроводности с использованием кусочно-квадратичной аппроксимации решения.

• Прокомментируйте процесс ансамблирования конечных элементов на примере стационарной задачи теплопроводности. Как учитываются граничные условия I, II и III рода при получении разрешающих соотношений?

• Сопоставьте варианты разрешающих соотношений, полученных на основе метода Галеркина, с использованием кусочно-линейной и кусочно-квадратичной аппроксимаций. Укажите достоинства и недостатки того и другого способов аппроксимации.

• С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения нестационарной теплопроводности с использованием кусочно-линейной аппроксимации решения.

• С помощью метода Галеркина постройте разрешающие соотношения для одномерного уравнения нестационарной теплопроводности с использованием кусочно-квадратичной аппроксимации решения.

• Укажите недостатки и достоинства приведенных в тексте схем аппроксимации производных по времени. Предложите иные разностные схемы аппроксимации производной по времени.