
- •Численные методы
- •Часть 3
- •Содержание
- •Введение
- •Классификация методов взвешенных невязок
- •Частные случаи метода взвешенных невязок
- •Метод моментов
- •Метод коллокаций
- •Метод подобластей
- •Метод наименьших квадратов
- •Метод конечных разностей
- •Расширение понятия функции
- •Пространство основных функций
- •Обобщенные функции
- •Дифференцирование обобщенных функций
- •Сходимость метода взвешенных невязок Основные понятия и определения
- •Обобщенное решение дифференциального уравнения
- •Сходимость метода конечных элементов
- •Контрольные вопросы и задания
- •Аппроксимация функций
- •Функции одной переменной
- •Кусочно-постоянные функции
- •Кусочно-линейные функции
- •Функции высших степеней
- •Иерархические многочлены
- •Функции двух переменных Треугольные конечные элементы. Линейная аппроксимация
- •Квадратичная аппроксимация
- •Четырехугольные конечные элементы
- •Функции трех переменных
- •Контрольные вопросы и задания
- •Задачи теплопроводности
- •Уравнение стационарной теплопроводности
- •Аппроксимация решения кусочно-линейными функциями
- •Процедура ансамблирования конечных элементов
- •Аппроксимация решения кусочно-квадратичными функциями
- •Использование иерархических многочленов
- •Уравнение нестационарной теплопроводности
- •Контрольные вопросы и задания
- •ЗадачИ механики деформируемого твердого тела Постановка задачи
- •Разрешающие соотношения метода взвешенных невязок Уравнение равновесия
- •Физические уравнения
- •Геометрические уравнения
- •Ансамблирование конечных элементов
- •Плоско-деформированное состояние
- •4 Узел 3 узел 3 узел
- •1 Элемент
- •2 Элемент
- •Плоско-напряженное состояние
- •Осесимметричное напряженно-деформированное состояние
- •Решение задач упругопластичности
- •Метод переменных параметров упругости
- •Метод дополнительных нагрузок
- •Контрольные вопросы и задания
- •ЗадачИ механики жидкости
- •Уравнения движения в переменных «функция тока – вихрь скорости»
- •Граничные условия
- •Граничные условия для функции тока
- •Граничные условия для функции завихренности
- •Соотношения метода взвешенных невязок
- •Разрешающие соотношения для функции тока
- •Разрешающие соотношения для функции завихренности
- •Разрешающие соотношения для поля давления
- •Алгоритм решения задачи
- •Контрольные вопросы и задания
- •Метод граничных элементов
- •Фундаментальное решение
- •Построение фундаментального решения
- •Контрольные вопросы и задания
- •Предметный указатель
- •Библиографический список
- •Приложение Бояршинов Михаил Геннадьевич Численные методы
- •Часть 3
Граничные условия
Поскольку в прикладных задачах краевые условия обычно ставятся в естественных переменных vx, vy и P, рассмотрим особенности постановки граничных условий для функций тока и завихренности.
Граничные условия для функции тока
Пусть ![]() – вектор единичной внешней нормали к
границе рассматриваемой
области ,
– вектор единичной внешней нормали к
границе рассматриваемой
области ,
![]() – единичный касательный вектор (рис.
5 .0). Проекции вектора
скорости на
– единичный касательный вектор (рис.
5 .0). Проекции вектора
скорости на
![]() и
и
![]() определяются выражениями
определяются выражениями
![]() ,
,
![]() .
.
Рис. 5.0. Схема расчетной
области
Из первого выражения следует, что
![]() .
.
Поскольку функция определяется с точностью до константы, граничные значения функции тока определяются выражением
![]() , (5.9)
, (5.9)
где s – дуговая
координата, отсчитываемая вдоль границы
Г от точки A, для которой
принято
![]() .
.
Граничные условия для функции завихренности
Для записи граничных условий для функции завихренности на твердой границе выбирается произвольная точка A. На расстоянии l от нее по нормали в глубь области выбирается точка B (рис. 5 .0). Вблизи точки B функция тока разлагается в ряд Тейлора
![]() .
.
Поскольку, как показано ранее,
![]() ,
и, согласно ( 5 .7),
,
и, согласно ( 5 .7),
![]() ,
,
получается
![]() .
.
Отсюда следует формула Тома [16] для функции завихренности,
![]() . (5.10)
. (5.10)
В частности,
![]() вдоль твердой границы, и формула ( 5 .10)
упрощается,
вдоль твердой границы, и формула ( 5 .10)
упрощается,
![]() .
.
Соотношения метода взвешенных невязок
Решения дифференциальных уравнений ( 5 .6) и ( 5 .7) в пределах отдельного треугольного конечного элемента представляются в форме
![]() ,
,
![]() ,
,
где, как и ранее, пробные кусочно-линейные функции для p-го конечного элемента имеют вид
![]() ,
,
![]() – узловые значения функций m
и m,
подлежащие определению.
– узловые значения функций m
и m,
подлежащие определению.
Разрешающие соотношения для функции тока
Пусть приближенное решение m
уравнения ( 5 .6) для некоторого момента
времени t
известно. Невязка уравнения ( 5 .7) на
приближенном решении m
взвешивается по области
p конечного элемента с
использованием тех же пробных функций
![]() ,
Остроградский
,
Остроградский
 .
.
Преобразования этого уравнения с использованием теоремы1 Остроградского2-Гаусса приводят к выражению

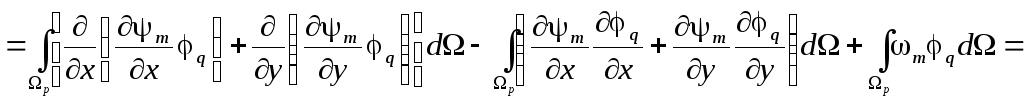
 .
.
Учитывая способ представления решений
m,
m
и соотношение
![]() ,
полученное выражение можно переписать
в виде
,
полученное выражение можно переписать
в виде
 .
.
С использованием обозначений
 ,
,

полученный результат удобно представить
в матричной форме в виде системы линейных
алгебраических уравнений относительно
узловых значений
![]() ,
,
![]() . (5.11)
. (5.11)
Разрешающие соотношения для функции завихренности
Пусть задача ( 5 .11) решена, то есть решение
m
уравнения ( 5 .7) найдено, в соответствии
с формулами ( 5 .1) вычислены компоненты
vx
и vy
вектора скорости. Невязка уравнения ( 5 .6)
на приближенном решении m
взвешивается по области
p конечного элемента с применением
пробных функций
![]() ,
,
 ,
,
 .
.
Слагаемые, входящие в это выражение, преобразуются с учетом представления приближенного решения m,
![]() ,
,
![]() ,
,


 .
.
Подстановка всех полученных слагаемых приводит к выражению
![]()
 .
.
Вводя дополнительные обозначения
 ,
,
полученное соотношение можно записать в матричном виде
![]() .
.
Использование разностной схемы Крэнка-Николсона
![]() ,
,
приводит к системе алгебраических
уравнений относительно узловых значений
![]() ,
,
![]() . (5.12)
. (5.12)
Разрешающие соотношения для поля давления
Пусть задачи ( 5 .11) и ( 5 .12) решены и функции
m
и m
определены, компоненты vx
и vy
вектора скорости найдены в соответствии
с выражениями ( 5 .1). Невязка уравнения
( 5 .8) взвешивается по области p
конечного элемента с применением пробных
функций
![]() ,
,
 .
.
Использование обозначений
![]() ,
,
и представления приближенного решения Pm в виде
![]() ,
,
позволяет получить систему уравнений для нахождения давления Pm в виде
 ,
,
 ,
,
 ,
,
 .
.
В матричной записи эта система линейных алгебраических уравнений записывается в форме
![]() , (5.13)
, (5.13)
где
 .
.
