
- •Численные методы
- •Часть 3
- •Содержание
- •Введение
- •Классификация методов взвешенных невязок
- •Частные случаи метода взвешенных невязок
- •Метод моментов
- •Метод коллокаций
- •Метод подобластей
- •Метод наименьших квадратов
- •Метод конечных разностей
- •Расширение понятия функции
- •Пространство основных функций
- •Обобщенные функции
- •Дифференцирование обобщенных функций
- •Сходимость метода взвешенных невязок Основные понятия и определения
- •Обобщенное решение дифференциального уравнения
- •Сходимость метода конечных элементов
- •Контрольные вопросы и задания
- •Аппроксимация функций
- •Функции одной переменной
- •Кусочно-постоянные функции
- •Кусочно-линейные функции
- •Функции высших степеней
- •Иерархические многочлены
- •Функции двух переменных Треугольные конечные элементы. Линейная аппроксимация
- •Квадратичная аппроксимация
- •Четырехугольные конечные элементы
- •Функции трех переменных
- •Контрольные вопросы и задания
- •Задачи теплопроводности
- •Уравнение стационарной теплопроводности
- •Аппроксимация решения кусочно-линейными функциями
- •Процедура ансамблирования конечных элементов
- •Аппроксимация решения кусочно-квадратичными функциями
- •Использование иерархических многочленов
- •Уравнение нестационарной теплопроводности
- •Контрольные вопросы и задания
- •ЗадачИ механики деформируемого твердого тела Постановка задачи
- •Разрешающие соотношения метода взвешенных невязок Уравнение равновесия
- •Физические уравнения
- •Геометрические уравнения
- •Ансамблирование конечных элементов
- •Плоско-деформированное состояние
- •4 Узел 3 узел 3 узел
- •1 Элемент
- •2 Элемент
- •Плоско-напряженное состояние
- •Осесимметричное напряженно-деформированное состояние
- •Решение задач упругопластичности
- •Метод переменных параметров упругости
- •Метод дополнительных нагрузок
- •Контрольные вопросы и задания
- •ЗадачИ механики жидкости
- •Уравнения движения в переменных «функция тока – вихрь скорости»
- •Граничные условия
- •Граничные условия для функции тока
- •Граничные условия для функции завихренности
- •Соотношения метода взвешенных невязок
- •Разрешающие соотношения для функции тока
- •Разрешающие соотношения для функции завихренности
- •Разрешающие соотношения для поля давления
- •Алгоритм решения задачи
- •Контрольные вопросы и задания
- •Метод граничных элементов
- •Фундаментальное решение
- •Построение фундаментального решения
- •Контрольные вопросы и задания
- •Предметный указатель
- •Библиографический список
- •Приложение Бояршинов Михаил Геннадьевич Численные методы
- •Часть 3
Аппроксимация решения кусочно-квадратичными функциями
Для решения той же задачи ( 3 .0)
– ( 3 .1) воспользуемся квадратичной
аппроксимацией в пределах одного
конечного элемента
![]() с центральной точкой xk.
Как и в предыдущем случае, решение
раскладывается по пробным функциям
с центральной точкой xk.
Как и в предыдущем случае, решение
раскладывается по пробным функциям
![]() , (3.12)
, (3.12)
имеющим вид
![]() .
.
Невязка уравнения ( 3 .0), получаемая на решении ( 3 .12), взвешивается с использованием тех же функций i, j и k,
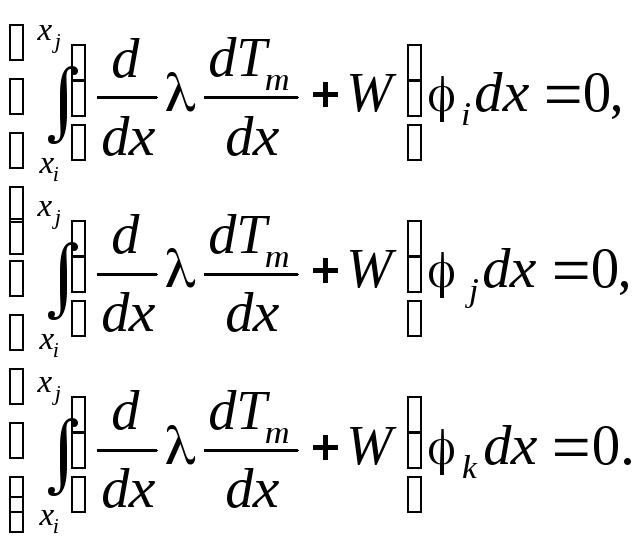 (3.13)
(3.13)
Преобразуем первое из этих уравнений:
 ,
,
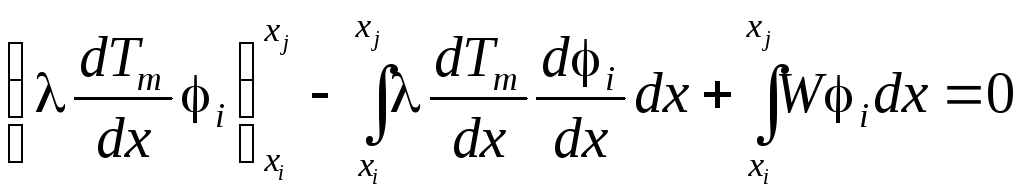 .
.
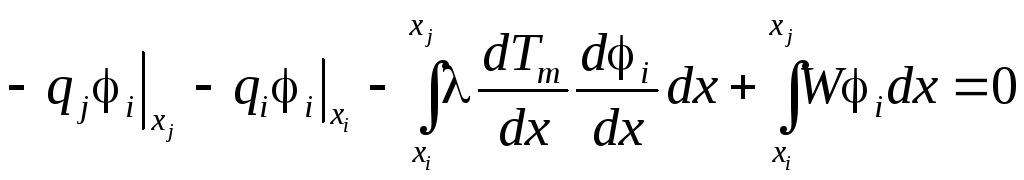 .
.
Учитывая, что
![]() ,
и используя разложение ( 3 .12), приходим
к выражению
,
и используя разложение ( 3 .12), приходим
к выражению
 .
.
Выполняя аналогичные преобразования с оставшимися выражениями в ( 3 .13), приходим к системе уравнений

Подсчитаем значения интегралов в полученных выражениях.
![]() ;
;
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Подстановка найденных значений приводит к системе уравнений

Эта же система в матричной форме принимает вид
 . (3.14)
. (3.14)
Суммируя все уравнения этой системы получаем
![]() ,
,
уже известное условие теплового баланса ( 3 .11).
Пример 3.2. Рассмотрим задачу из
примера 3.1 с теми же исходными данными.
Пусть весь стержень аппроксимируется
одним конечным элементом. Будем считать,
как и в предыдущем случае, что на его
левом конце задана температура
![]() ,
а на правом – граничные условия третьего
рода
,
а на правом – граничные условия третьего
рода
![]() .
.
Для рассматриваемого случая система уравнений приводится к виду
 ,
,
Для принятых L, W, ,
![]() и эта система
уравнений принимает вид
и эта система
уравнений принимает вид

и имеет решение Ti=100 (левый конец стержня), Tj = 153/2 (правый конец), Tk = 619/7 (центр стержня). С учетом вида пробных функций ( 3 .2) решение запишется в виде
![]() .
.
Полученное выражение является точным решением этой задачи.
Использование иерархических многочленов
Для построения решения задачи ( 3 .0)
– ( 3 .1) на конечном элементе
![]() вводятся локальные координаты ,
с помощью которых строятся иерархические
многочлены
вводятся локальные координаты ,
с помощью которых строятся иерархические
многочлены
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…
,
…
Первоначально решение строится в виде
![]() .
.
Невязка уравнения теплопроводности ( 3 .0),
получаемая на этом решении, взвешивается
по области
![]() поочередно с каждой из функций 0,
1 и 2,
поочередно с каждой из функций 0,
1 и 2,

Учитывая, что
![]() ,
,
подсчитываются значения интегралов, входящих в эту систему уравнений,
![]() ,
,
![]() ,
,
![]() .
.
Подстановка полученных коэффициентов приводит к системе уравнений

В матричной форме эта система уравнений имеет вид
 . (3.15)
. (3.15)
Теперь рассмотрим вариант аппроксимации решения в виде
![]() .
.
Взвешенные по области
![]() невязки уравнения теплопроводности ( 3 .0)
приводят к системе уравнений
невязки уравнения теплопроводности ( 3 .0)
приводят к системе уравнений

Поскольку
![]() ,
можно определить значения интегралов,
которые дополнительно входят во вновь
сформированную систему уравнений,
,
можно определить значения интегралов,
которые дополнительно входят во вновь
сформированную систему уравнений,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Подстановка коэффициенты приводит к системе уравнений

которая в матричном представлении имеет вид
 . (3.16)
. (3.16)
И, наконец, рассмотрим аппроксимацию решения задачи ( 3 .0) в виде
![]() .
.
Выполнение преобразований, аналогичных показанных выше, приводит в конечном итоге к системе линейных алгебраических уравнений
 . (3.17)
. (3.17)
Необходимо отметить, что при аппроксимации решения задачи ( 3 .0) – ( 3 .1) с помощью кусочно-линейного ( 3 .3) и кусочно-квадратичного ( 3 .12) приближений соответствующие системы уравнений ( 3 .8) и ( 3 .14) совершенно различны.
Системы уравнений ( 3 .15), ( 3 .16) и ( 3 .17), полученные при аппроксимации решения той же задачи с помощью иерархической системы функций с 3, 4 и 5 слагаемыми, соответственно, отличаются лишь дополнительными строками и столбцами (выделены жирным шрифтом). Иными словами, при использовании иерархической системы функций для повышении порядка аппроксимации решения достаточно лишь расширить систему линейных алгебраических уравнений дополнительными слагаемыми.
