
- •Численные методы
- •Часть 3
- •Содержание
- •Введение
- •Классификация методов взвешенных невязок
- •Частные случаи метода взвешенных невязок
- •Метод моментов
- •Метод коллокаций
- •Метод подобластей
- •Метод наименьших квадратов
- •Метод конечных разностей
- •Расширение понятия функции
- •Пространство основных функций
- •Обобщенные функции
- •Дифференцирование обобщенных функций
- •Сходимость метода взвешенных невязок Основные понятия и определения
- •Обобщенное решение дифференциального уравнения
- •Сходимость метода конечных элементов
- •Контрольные вопросы и задания
- •Аппроксимация функций
- •Функции одной переменной
- •Кусочно-постоянные функции
- •Кусочно-линейные функции
- •Функции высших степеней
- •Иерархические многочлены
- •Функции двух переменных Треугольные конечные элементы. Линейная аппроксимация
- •Квадратичная аппроксимация
- •Четырехугольные конечные элементы
- •Функции трех переменных
- •Контрольные вопросы и задания
- •Задачи теплопроводности
- •Уравнение стационарной теплопроводности
- •Аппроксимация решения кусочно-линейными функциями
- •Процедура ансамблирования конечных элементов
- •Аппроксимация решения кусочно-квадратичными функциями
- •Использование иерархических многочленов
- •Уравнение нестационарной теплопроводности
- •Контрольные вопросы и задания
- •ЗадачИ механики деформируемого твердого тела Постановка задачи
- •Разрешающие соотношения метода взвешенных невязок Уравнение равновесия
- •Физические уравнения
- •Геометрические уравнения
- •Ансамблирование конечных элементов
- •Плоско-деформированное состояние
- •4 Узел 3 узел 3 узел
- •1 Элемент
- •2 Элемент
- •Плоско-напряженное состояние
- •Осесимметричное напряженно-деформированное состояние
- •Решение задач упругопластичности
- •Метод переменных параметров упругости
- •Метод дополнительных нагрузок
- •Контрольные вопросы и задания
- •ЗадачИ механики жидкости
- •Уравнения движения в переменных «функция тока – вихрь скорости»
- •Граничные условия
- •Граничные условия для функции тока
- •Граничные условия для функции завихренности
- •Соотношения метода взвешенных невязок
- •Разрешающие соотношения для функции тока
- •Разрешающие соотношения для функции завихренности
- •Разрешающие соотношения для поля давления
- •Алгоритм решения задачи
- •Контрольные вопросы и задания
- •Метод граничных элементов
- •Фундаментальное решение
- •Построение фундаментального решения
- •Контрольные вопросы и задания
- •Предметный указатель
- •Библиографический список
- •Приложение Бояршинов Михаил Геннадьевич Численные методы
- •Часть 3
Процедура ансамблирования конечных элементов
Рассмотрим композицию из четырех конечных элементов, для каждого из которых запишем свою систему уравнений ( 3 .7):
 Q0
q2
Q0
q2 
![]() q3
q3 
![]() q4
q4 
![]() Q1
Q1 
В итоге получена система восьми
алгебраических уравнений с одиннадцатью
неизвестными
![]() .
Для замыкания системы уравнений следует
добавить три дополнительных уравнения
теплового баланса
.
Для замыкания системы уравнений следует
добавить три дополнительных уравнения
теплового баланса
 (3.9)
(3.9)
Отметим, что внутренние переменные
![]() можно исключить из системы уравнений,
складывая уравнения попарно и используя
равенства ( 3 .9). Так, для двух первых
систем уравнений получаем
можно исключить из системы уравнений,
складывая уравнения попарно и используя
равенства ( 3 .9). Так, для двух первых
систем уравнений получаем

Складывая второе и третье уравнения системы, с учетом ( 3 .9) получаем

Выполняя аналогичные преобразования
для всех уравнений системы, приходим к
системе пяти уравнений относительно
пяти неизвестных
![]()

В матричной форме эта система уравнений имеет вид
 . (3.10)
. (3.10)
Рассмотрим неоднородную систему алгебраических уравнений ( 3 .7),
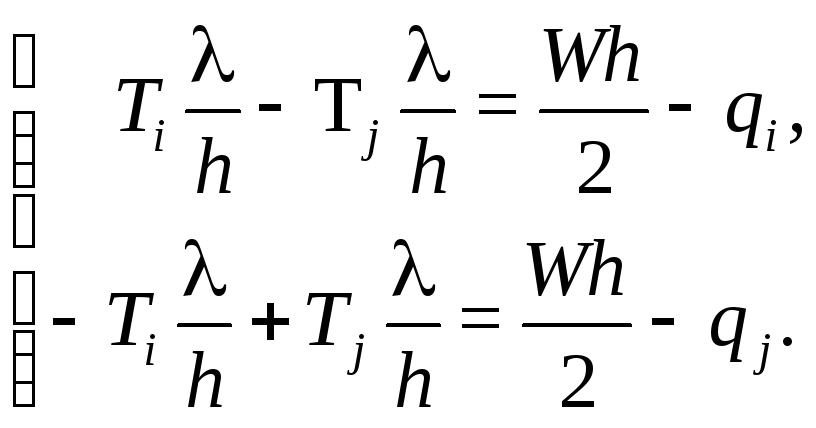
Легко проверить, что ее определитель равен нулю. Точно так же равен нулю определитель системы алгебраических уравнений ( 3 .10). Складывая покомпонентно оба уравнения последней системы, получаем выражение
![]() , (3.11)
, (3.11)
являющееся условием баланса тепла в
отдельном конечном элементе: количество
тепла, выделившееся за счет внутренних
источников, должно быть выведено из
него за счет тепловых потоков с торцов.
Это становится очевидным, если вспомнить,
что решается стационарное уравнение
теплопроводности, решение которого
может рассматриваться как температурное
поле, установившееся за бесконечно
большой промежуток времени. Невыполнение
балансового соотношения ( 3 .11) приведет
либо к накоплению тепла в стержне (при
![]() )
и, следовательно, к бесконечно высоким
температурам, либо к принудительному
отводу тепла из стержня (при
)
и, следовательно, к бесконечно высоким
температурам, либо к принудительному
отводу тепла из стержня (при
![]() )
и, соответственно, к бесконечно низким
температурам. При точном выполнении
соотношения ( 3 .11) стержень будет
находиться в состоянии термического
равновесия при любых значениях
температур. Это означает, что решение
оказывается неединственным, то есть
исходная задача сформулирована
некорректно. Это очевидно из уравнений
( 3 .0) – ( 3 .1), которые определяют решение
с точностью до постоянной величины.
)
и, соответственно, к бесконечно низким
температурам. При точном выполнении
соотношения ( 3 .11) стержень будет
находиться в состоянии термического
равновесия при любых значениях
температур. Это означает, что решение
оказывается неединственным, то есть
исходная задача сформулирована
некорректно. Это очевидно из уравнений
( 3 .0) – ( 3 .1), которые определяют решение
с точностью до постоянной величины.
Вырожденность системы уравнений на
элементарном уровне ( 3 .7) приводит
к вырожденности системы алгебраических
уравнений ( 3 .10) для всего ансамбля
конечных элементов. Легко установить,
что и в этом случае суммирование всех
уравнений системы ( 3 .10) приводит к
балансовому соотношению
![]() .
Несмотря на некорректность задачи
( 3 .0) – ( 3 .1) рассмотренный порядок
построения разрешающих соотношений
является верным и используется для
нахождения численного решения. Для
корректной постановки задачи следует
изменить граничные условия. Пусть на
левом конце стержня поддерживается
постоянная температура
.
Несмотря на некорректность задачи
( 3 .0) – ( 3 .1) рассмотренный порядок
построения разрешающих соотношений
является верным и используется для
нахождения численного решения. Для
корректной постановки задачи следует
изменить граничные условия. Пусть на
левом конце стержня поддерживается
постоянная температура
![]() .
Для учета этого граничного условия к
полученной системе ( 3 .10) следует добавить
уравнение
.
Для учета этого граничного условия к
полученной системе ( 3 .10) следует добавить
уравнение
![]()
(искомый коэффициент T1, как
это уже отмечалось ранее, аппроксимирует
значение искомой температуры в этом
узле) и считать поток Q0
на левом конце стержня неизвестным.
В этом случае получена система шести
уравнений с неизвестными
![]() ,
имеющая ненулевой определитель,
,
имеющая ненулевой определитель,

На практике уравнение, содержащее неизвестный поток Q0, как правило, исключается из системы уравнений,

В дальнейшем, после определения всех
узловых температур
![]() ,
исключенное из системы уравнение
,
исключенное из системы уравнение
![]()
может быть использовано для определения теплового потока
![]() .
.
В матричной форме преобразованная система уравнений имеет вид
 .
.
При решении прикладных инженерных задач на границе рассматриваемой области могут быть заданы условия конвективного теплообмена, когда на правом конце стержня тепловой поток равен
![]() ,
,
где – коэффициент теплоотдачи с поверхности в окружающую среду с температурой T , то есть имеет место граничное условие третьего рода,
![]() .
.
Для включения этого граничного условия
в полученную систему уравнений следует
выполнить замену в последнем уравнении,
учитывая, что
![]() :
:
![]() ,
,
![]() .
.
В результате всех преобразований система линейных алгебраических уравнений преобразуется к виду
 . (3.11)
. (3.11)
Пример 3.1. Решим полученную систему
линейных алгебраических уравнений при
следующих данных. Пусть длина стального
стержня L = 1 м; мощность внутренних
тепловых источников W = 100 Вт/м3,
коэффициент теплопроводности стали
= 70 Вт/мград,
температура окружающей среды
![]() ,
,
![]() ,
= 30 Вт/м2град.
Система уравнений принимает вид
,
= 30 Вт/м2град.
Система уравнений принимает вид
 .
.
Решение этой системы
T1 = 100, T2 = 10557/112, T3 = 619/7, T4 = 9241/112, T5 = 153/2
в узловых точках тождественно удовлетворяет точному решению задачи
![]() .
.
Величина теплового потока на левом конце стержня
![]() Вт/м2 .
Вт/м2 .
Используя точное решение задачи, определяем производную
![]() ,
,
и, подставляя x = 0, находим точное значение теплового потока
![]() Вт/м2 .
Вт/м2 .
