6. Зв’язані контури

Як відомо, ідеальний фільтр повинен мати П - подібну частотну характеристику та лінійну фазову характеристику в межах смуги пропускання. Для розв’язку багатьох радіотехнічних задач необхідні фільтри, частотна характеристика яких в більшому ступені, ніж в звичайному коливальному контурі, наближується до ідеальної. В радіодіапазоні при створенні таких фільтрів використовується система декількох контурів, зв’язаних між собою або магнітним загальним полем (індуктивний зв’язок), або загальним електричним полем (ємнісний зв’язок).

Розглянемо випадок двох контурів з індуктивним зв’язком. Тут * – означає той факт, що котушки ввімкнені таким чином, що при однаковому напрямку струму магнітні потоки додавалися. Використаємо другий закон Кіргофа

де,

Зрозуміло, що миттєві значення

, (2)

Якщо синусоїдальна, то та також. Тобто, похідні за часом будуть мати множник . Разом з тим, та відстають від та на фазовий кут, що дорівнює 90^о (див. трансформатор), а величини - та - випереджають ці струми на 90^о . Переходячи до комплексних значень, будемо мати

, (3)

Тепер (1) можна записати :

де (4)

, ,

, . (5)

Будемо вважати, що контури тут тотожні, тобто

, , , (6)

тоді

, (7)

якщо .

Позначимо

, де f - лінійна частота (8)

Тоді

(9)

і

(10)

Величину - назв. параметром зв’язку контурів

-----обрив-------------

(14)

Розглянемо ряд випадків.

1/ - зв’язок між контурами слабкий. Взагалі залежить

від частоти , але при невеликих розстрочках цей параметр можна

вважати сталим.

При =0 // підкореневий вираз набуває мінімального зна-

чення, а струм I - максимального. В цьому випадку має місце

явище резонансу. Резонансе значення струму дорівнює

(15)

2/ - зв’язок між контурами критичний,

тут при // підкореневий вираз

набуває мінімального значення, а струм І

максимального

I (16)

3/ - зв’язок сильний. Розглянемо докладно функцію

(17)

Дослідимо на екстремум:

, , , (18)

, (19)

При , досягає максимального значення, а струм – мінімальний

I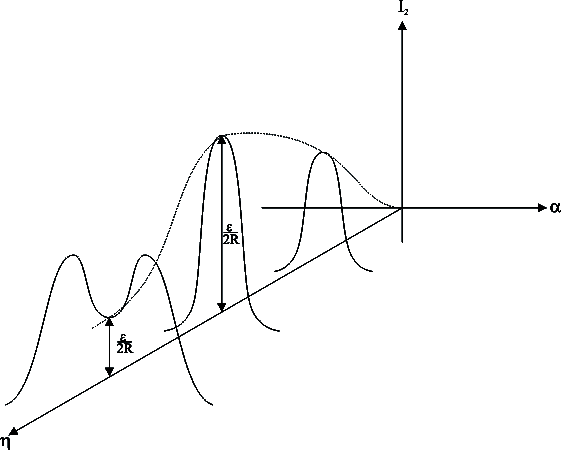 , (20)

При , , а I , т. як

І (21) Тепер, вже І=І можна подати у вигляді системи графіків.

Таким чином, при ‘докритичному’ зв’язку // резонансна характеристика має один максимум. При зв’язку, що перевищує критичний, резонансна характеристика перетворюється на ‘двогорбу’, причому на основній частоті резонансу є мінімум. Цей факт не повинен нас бентежити, оскільки головною ознакою резонансу є збіг за фазою струму і е.р.с. в контурі.

При збільшені зв’язку форма резонансної характеристики фільтра

поліпшується, наближуючись до прямокутної, але не буде ідеальною.

Якщо ‘западина’ виявиться на рівні y=0,7 , то смуга пропускання одиночного контура зв’язаних контурів, як можна довести, перевищіть смугу пропускання одиночного контура у 3,1 раза.

Таким чином, при зміні зв’язку між контурами і доборі потрібних контурів можна дістати задану смугу пропускання при задовільній формі резонансної характеристики.