Определение относительной погрешности косвенных измерений

Мы уже отмечали, что часто бывает удобно сначала определить относительную погрешность косвенного измерения , а затем абсолютную. Покажем это на примерах.

Пример. Пусть x, y и z – прямо измеренные величины, а f – косвенно определяемая через них величина. Вывести формулы для определения относительной погрешности косвенных измерений:

а) f=(xy)^z; б) f=sin(x²+y²); в) .

Значения , , и считать известными.

Решение:

Напомним, что рассчитывается по формуле:

.

а) Сначала прологарифмируем функцию f=(xy)^z :

.

Теперь найдем частные производные , и :

;

;

.

Тогда:

,

.

Теперь, зная и , рассчитаем :

.

б) Прологарифмировав данную функцию f=sin(x²+y²), получим:

. Мы видим, что выражение лишь усложнилось, искать производную от исходной функции проще, чем от ее логарифма. Поэтому запишем частные производные функции:

; .

Подставим эти данные в формулу для определения абсолютной погрешности косвенного измерения. Напомним, что рассчитывается так:.Получим:

.

Теперь, зная и , можно рассчитать :

.

в) В этом примере исходную функцию удобно прологарифмировать:

.

Теперь будет проще искать частные производные. Итак:

,

,

.

Подставим полученные значения в формулу для определения . Получим:

,

.

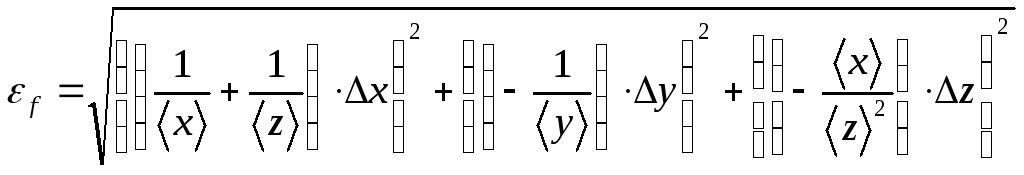Теперь, зная и , рассчитаем : .

ПРИЛОЖЕНИЕ 5

Погрешности элементарных функций

Таблица 4

№	Вид функции z = z(a)	Абсолютная погрешность z	Относительная погрешность
1	ca, c = const	ca
2
3
4
5
6
7
8
9
10
11
12

Наиболее часто встречаются следующие случаи определения погрешностей:

1. Погрешности в суммах и разностях. Если а₁ и а₂ измерены с погрешностями Δа₁ и Δа₂ и измеренные значения используются для вычисления суммы или разности А = а₁ ± а₂, то суммируются абсолютные погрешности (без учета знака):

ΔА = Δа₁ + Δа₂.

2. Погрешности в произведениях и частных. Если измеренные значения а₁ и а₂ используются для вычисления А = а₁  а₂ или А = а₁ / а₂, то суммируются относительные погрешности:

ε_А = ε_а1 + ε_а2, где ε = Δа / а.

3. Измеренная величина умножается на точное число. Если а используется для вычисления произведения А = В  а, в котором В не имеет погрешности, то А = | В |  ε_а.

4. Возведение в степень. Если а используется для вычисления степени А = аⁿ, то А = n  ε_а.

5. Погрешности в произвольной функции одной переменной. Если а используется для вычисления функции А(а), то:

.

Пример 1. Производится косвенное измерение электрической мощности, рассеиваемой на резисторе сопротивлением R при протекании по нему тока I. Так как P = I²  R, то, применяя правила 2 и 4, получим ε_P = ε_R + 2ε_I.

Пример 2. Измерением найдено значение угла α = (20±3). Необходимо найти cosα. Наилучшая оценка для cos20 = 0,94. Погрешности Δα = 3 = 0,05 рад. Тогда по правилу 5 имеем ε_cosα = (sin20)  0,05 = 0,34  0,05 = 0,02. Окончательно cosα = 0,94 ± 0,02.

ПРИЛОЖЕНИЕ 6

В приведенной таблице представлены экспериментальные данные, с помощью которых можно определить сопротивление некоторого образца:

Таблица 5

I, мА	U, В	I2,( мА)2	U2, В2	IU, мАВ
12,1	2,7	146,41	7,29	32,67
15,9	3,3	252,81	10,98	52,47
21,8	3,2	475,24	10,24	69,76
25,0	3,2	625,00	10,24	80,00
29,8	3,5	888,04	12,25	104,30
33,5	4,3	1122,25	18,49	144,05
38,3	4,0	1466,89	16,00	153,20
41,0	4,6	1681,00	21,16	188,60
46,6	5,1	2171,56	26,01	237,66
54,8	5,1	3003,04	26,01	279,48

1. В качестве переменной x выступает сила тока I, переменной y является напряжение U. По формулам и вычисляют средние значения переменных:,

.

2. По формулам и вычисляют средние квадраты:

,

3. Рассчитывают <xy> как :

4. Определить оптимальные значения коэффициентов а и b по формулам:

,

,

.

5. Определяют квадрат среднего квадратичного отклонения σ²:

4.Определить квадраты средних квадратичных отклонений σ_а² и σ_b²:

, .

,

5. Вычислить погрешности и :

, .

ПРИЛОЖЕНИЕ 7

Значения t_α,n для различных значений доверительной вероятности

α и числа измерений n (распределение Стьюдента)

Таблица 6

α n	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99	0,999
2	1,000	1,376	1,963	3,08	6,31	12,71	31,8	63,7	636,6
3	0,816	1,061	1,336	1,886	2,92	4,30	6,96	9,92	31,6
4	0,765	0,978	1,250	1,638	2,35	3,18	4,54	5,84	12,94
5	0,741	0,941	1,190	1,533	2,13	2,77	3,75	4,60	8,61
6	0,727	0,920	1,156	1,476	2,02	2,57	3,36	4,03	6,86
7	0,718	0,906	1,134	1,440	1,943	2,45	3,14	4,71	5,96
8	0,711	0,896	1,119	1,415	1,895	2,36	3,00	3,50	5,40
9	0,706	0,889	1,108	1,397	1,860	2,31	2,90	3,36	5,04
10	0,703	0,883	1,110	1,383	1,833	2,26	2,82	3,25	4,78
11	0,700	0,879	1,093	1,372	1,812	2,23	2,76	3,17	4,59
12	0,697	0,876	1,088	1,363	1,796	2,20	2,72	3,11	4,49
13	0,695	0,873	1,083	1,356	1,782	2,18	2,68	3,06	4,32
14	0,694	0,870	1,079	1,350	1,771	2,16	2,65	3,01	4,22
15	0,692	0,868	1,076	1,345	1,761	2,14	2,62	2,98	4,14
16	0,691	0,866	1,074	1,341	1,753	2,13	2,60	2,95	4,07
17	0,690	0,868	1,071	1,337	1,746	2,12	2,58	2,92	4,02
18	0,689	0,863	1,069	1,333	1,740	2,11	2,57	2,92	3,96
19	0,688	0,862	1,067	1,330	1,734	2,10	2,55	2,88	3,92
20	0,688	0,861	1,066	1,328	1,729	2,09	2,54	2,86	3,88
	0,674	0,842	1,036	1,282	1,645	1,960	2,33	2,58	3,29

1 Более подробно о классе точности прибора см. Сысоев С.М. Лабораторный практикум по электричеству и магнетизму: Методические указания к лабораторным работам по курсу общей физики. Для студентов всех специальностей / Сысоев С.М., Манина Е.А., Никонова Н.О.; Под ред. С.М. Сысоева. – Сургут: Изд-во СурГУ, 2004.

52