1. Что такое поверхность?

Поверхности – это объекты, которые чаще всего представляются значениями высоты Z, распределенными по области, определенной координатами X и Y. Параметр Z чаще всего ассоциируется с высотой рельефа местности, но не обязательно. На самом деле, любые измеримые величины, которые могут встречаться на определенной территории, могут рассматриваться как образующие поверхность. Обычно используется термин "статистическая поверхность" , поскольку значения параметра Z часто можно трактовать как статистическое представление величины рассматриваемых явлений или объектов. Например, таких как плотность населения, доход, плотность животных, атмосферное давление и др..

За статистическими поверхностями стоит идея о том, что z-величина либо непрерывна по интересующей нас области, либо может считаться непрерывной в целях моделирования и картографирования. Статистические поверхности, образованные величиной, определенной во всех точках изучаемой области, называются непрерывными (continuous). Те же, что встречаются только индивидуально, но с некоторым различием в числе на единицу площади (такие, как число домов на квадратный километр в каждой окрестности), называются дискретными. Рассмотрим эти статистические поверхности по отдельности.

Говорят, что непрерывные данные присутствуют в каждой возможной точке области, – существует возможность получения отсчета этой величины на сколь угодно малой площади где угодно в рассматриваемой области. Мы знаем, например, что температура имеется повсюду. Мы можем измерить ее в любой точке. Если мы это сделаем, то увидим, что она постепенно меняется от точки к точке непрерывной последовательностью. В некоторых случаях эти изменения невелики, возможно, менее чем на одну десятую градуса через 100 метров. Мы говорим, что имеем дело с гладкой поверхностью, с небольшим изменением статистической информации на единицу расстояния. Однако, в других случаях, например, когда мы пересекаем границу между двумя различными воздушными массами, значения температуры резко меняются. Такую поверхность называют неровной, поскольку имеется резкое изменение статистических данных на небольшом расстоянии.

Определение статистической поверхности как непрерывной означает, что имеется бесконечное количество точек, в каждой из которых может быть свое значение. Однако, провести измерения в бесконечном числе точек – физически невозможно, также как невозможно хранить бесконечный объем данных. Поэтому определение непрерывной поверхности с помощью бесконечного числа точек должно быть заменено моделью, которая использует выборочный набор рассматриваемой величины.

1. Изображение поверхностей на картах

Статистические поверхности могут представляться посредством плотности точек, хороплет, дасиметрии и изолиний. Первые три чаще всего имеют дело с дискретными поверхностями. Четвертый метод наиболее часто используется для непрерывных данных, хотя он может использоваться и для дискретных данных, если условно представить их непрерывными. Изолинии представляют собой последовательность линий, покрывающих топографическую поверхность. Каждая линия, обычно называемая горизонталью в топографическом контексте, представляет все точки, имеющие одну и ту же высоту. Общее название линий, соединяющих точки одинаковых значений статистической величины, – изолиния.

При взгляде сверху изолинии выглядят как последовательность непересекающихся линий. Если они представляют топографический объект такой как холм, то они замкнуты и очерчивают объект; если нет, то продолжаются до краев карты. То, что мы видим, есть линейные символы для отображения поверхностных данных. Более того, они позволяют нам наблюдать конкретные формы рельефа местности. Например, горизонтали, пересекающие речные долины, обычно выглядят как буква V, указывающая вверх по течению; на крутых склонах горизонтали расположены более плотно по сравнению с пологими склонами. Горизонтали могут применяться для представления уклона (рисунок 1.23).

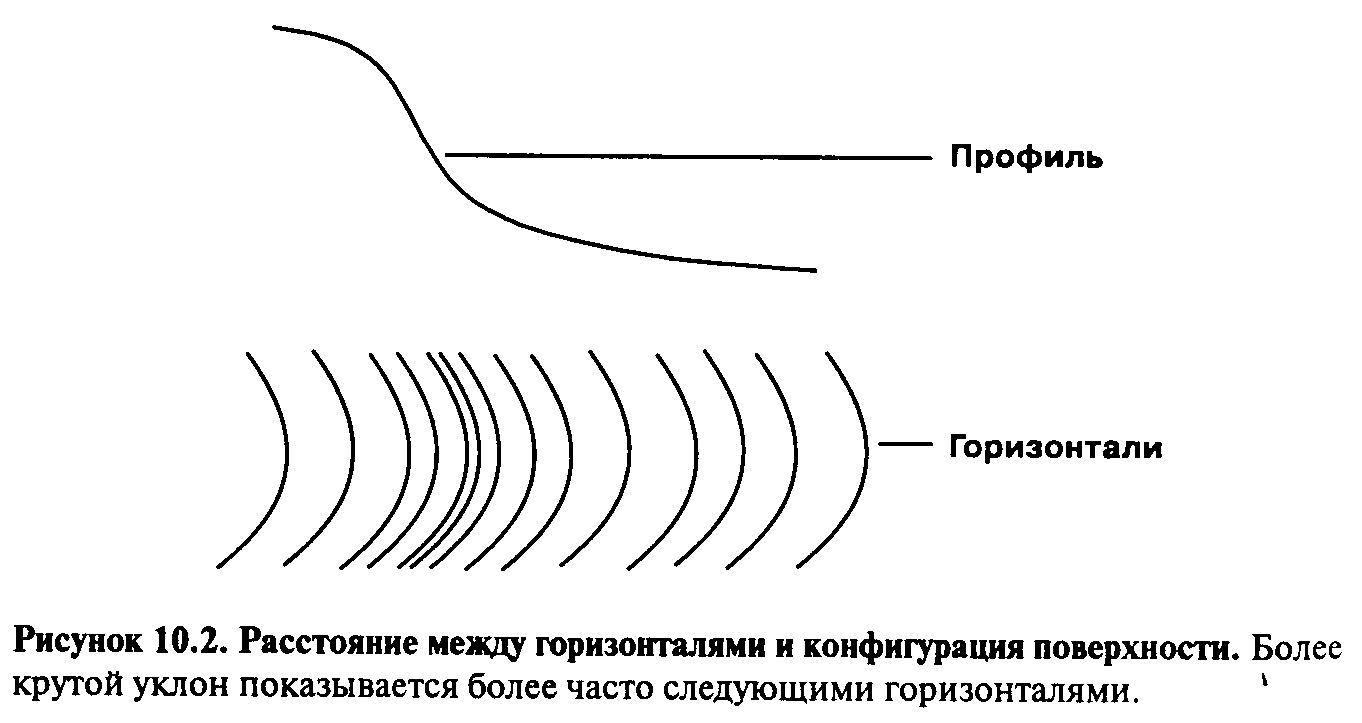
Рисунок 1.23 ‑ Расстояние между горизонталями и конфигурация поверхности. Более крутой уклон показан более часто следующими горизонталями.

Расстояние по вертикали между любыми горизонталями одинаково, и это не случайно. Расстояние по вертикали выбирается таким, чтобы пользователю карту было легче понимать, что эти линии представляют. Каждая карта имеет собственное вертикальное расстояние между горизонталями, в зависимости от быстроты изменения высоты. Эта величина, называемая интервалом между изолиниями (contour interval), используется для деления (или квантования) изменения Z-величины на равные интервалы высот. Если бы использовались разные интервалы между соседними горизонталями, то не невозможно было бы интерпретировать частоту их следования как показатель уклона.