Опис експериментальної установки та хід виконання роботи

1. Експериментальна установка складається з модуля ФПЕ–03, блока живлення (БЖ), міліамперметра. Принципова схема представлена на рис.4.

2

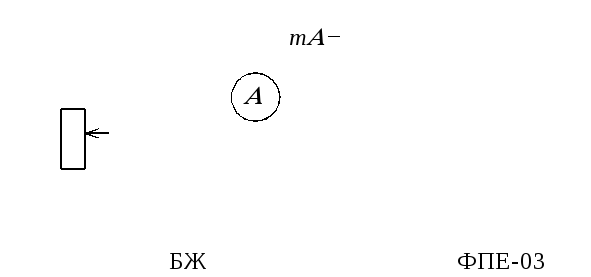Рис.4

. Скласти схему, показану на рис.4.

3. Встановити анодну напругу по вольтметру блока живлення.

4. Змінюючи силу струму в соленоїді при постійній анодній напрузі, зняти залежність анодного струму від струму соленоїда . Дані занести в таблицю.

5. Побудувати графік залежності і визначити на ньому критичний струм . Значення вибирається на кривій в точці, де починає спадати.

6. Обчислити відносну і абсолютну похибки вимірювання питомого заряду. Користуючись паспортними даними приладів, відносну похибку можна обчислити за формулою

.

Абсолютна похибка обчислюється за формулою.

.

7. Записати кінцевий результат.

Таблиця вимірювань

U=, l=, d=, R=, N=, μ_0=, I_ск=

_ΔU₀=, _Δl₀=, _Δd₀=, _ΔR₀=, _ΔN0=, _Δ(μ₀₎₀=, _Δ(I_ск)₀=

Контрольні запитання

1. Яка будова магнетрона? Практичне використання магнетрона.

2. Описати електромагнітне поле в магнетроні.

3. Довести, що сила Лоренца не виконує роботи.

4. При яких умовах виникає сила Лоренца? Яка величина і напрям сили Лоренца?

5. Чому в залежності відсутній різкий спад?

6. Вивести робочу формулу.

Лабораторна робота № 4.4 Вивчення магнітного поля соленоїда за допомогою датчика Холла

Мета роботи: ознайомитися з холлівським методом вимірювання індукції магнітного поля; дослідити залежність індукції магнітного поля в центрі соленоїда від струму; дослідити осьову неоднорідність магнітного поля в соленоїді.

Теоретичні відомості

(теорію до даної роботи див. також у конспекті лекцій, §§4.2-4.3)

1

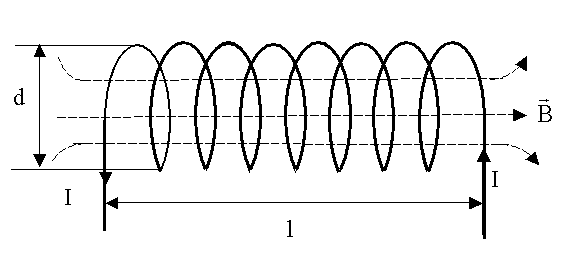Рис.1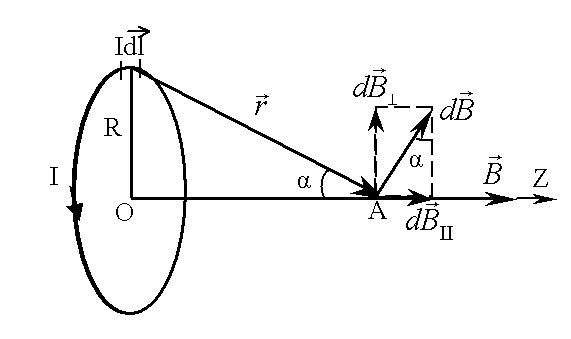

Рис.2

. Соленоїд є системою послідовно з’єднаних однакових колових струмів (рис.1), тому для розрахунку індукції В магнітного поля в довільній точці на осі соленоїда потрібно спочатку розглянути магнітне поле на осі колового струму (одного витка соленоїда) (рис.2). Виберемо елемент струму . Вектор індукції магнітного поля, породженого цим елементом в точці А, положення котрої задається радіус-вектором , визначається законом Біо-Савара-Лапласа (у вакуумі)

, (1)

де – магнітна стала. При цьому можна розкласти на дві складові: – паралельну до осі Z і – перпендикулярну до цієї осі. За принципом суперпозиції вектор індукції магнітного поля, створеного коловим струмом, тобто усіма елементами струму,

. (2)

Тут враховано, що для усякого елементу знайдеться симетричний елемент, що дає складову протилежного напрямку. Якщо врахувати, що усіх елементів напрямлені вздовж осі Z, а також, що і , то після підстановки (1) у (2) отримаємо для індукції магнітного поля на осі колового струму

. (3)

Зауважимо, що в центрі колового струму ()

.

2

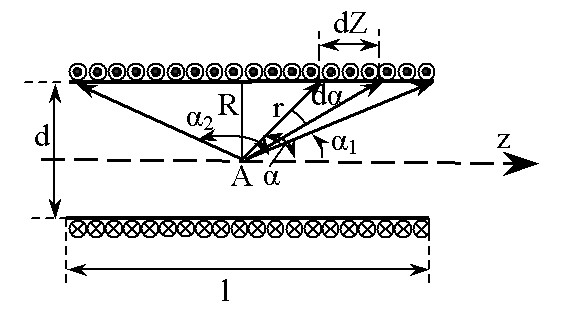Рис.3

. Для розрахунку індукції магнітного поля соленоїда розглянемо його осьовий переріз (рис.3),припускаючи постійність щільності намотки вздовж осі Z. Якщо на одиницю довжини соленоїда припадає n витків, то на ділянці довжиною dz буде ndz витків, які в точці А створять магнітне поле з індукцією

. (4)

Врахувавши, що , , після інтегрування (4) по всій довжині соленоїда отримаємо для індукції магнітного поля на осі соленоїда

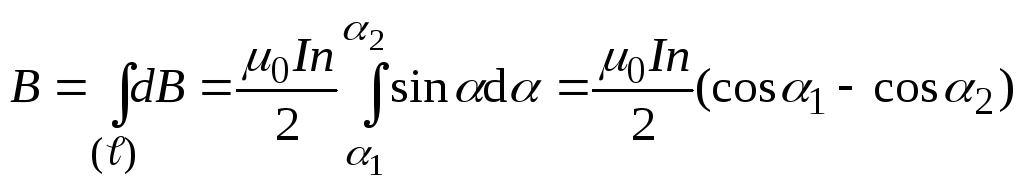. (5)

Якщо соленоїд дуже довгий , то і . Тоді

. (6)

Зауважимо, що формулу (6) можна отримати, використавши теорему про циркуляцію вектора індукції магнітного поля. Для дуже довгого соленоїда магнітне поле практично однорідне (силові лінії еквідистантні і паралельні до осі соленоїда). Для реальних соленоїдів, коли нерівність слабка, поле найсильніше в центрі соленоїда і зменшується при наближенні до його кінців.

3

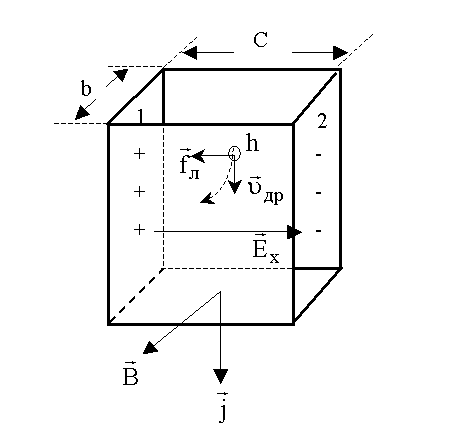Рис.4

. Для визначення індукції магнітного поля на осі соленоїда в цій роботі використовуються напівпровідникові датчики, дія яких грунтується на ефекті Холла,–датчики Холла (ДХ) (рис.4). Нехай для ДХ використано напівпровідниковий кристал з дірковою провідністю (носії струму – дірки (hole)). Якщо вздовж такого кристалу протікає електричний струм з густиною і він розміщений в поперечному магнітному полі з індукцією , то на носії струму, заряд яких е, і які рухаються з дрейфовою швидкістю , буде діяти сила Лоренца

. (7)

Ця сила, як видно з рис.4, буде відхиляти носії до грані 1, і між гранями 1 та 2 виникне поперечне холлівське поле з напруженістю , значення якої визначене з умови рівноваги становить

. (8)

Різниця потенціалів між гранями 1, 2 або холлівська напруга складає

. (9)

Якщо врахувати, що густина струму пов’язана з і концентрацією носіїв Р співвідношенням , то (9) перепишеться як

, (10)

де І – сила струму через кристал, а – постійна Холла.

О

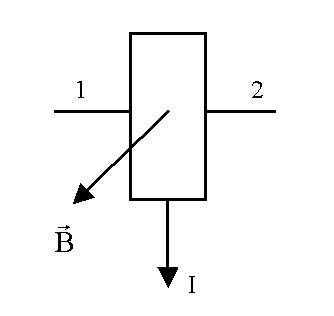Рис.5

скільки значення i є фіксованими параметрами ДХ, а сила струму через кристал підтримується постійною (для ДХ цієї роботи ), то доцільно ввести коефіцієнт пропорційності , і тоді (10) запишеться як

. (11)

Отже, для визначення значення індукції магнітного поля соленоїда достатньо виміряти холлівську напругу між контактами 1–2 ДХ (рис.5) і помножити її на . Ситуація дещо ускладнюється можливою нееквіпотенціальністю контактів 1, 2, що приво-дить до появи напруги нееквіпотенціальностї навіть при відсутності магнітного поля. В цьому випадку

(12)

де – напруга, що вимірюється вольтметром з великим вхідним опором (чи потенціометром), приєднаним безпосередньо до контактів 1, 2 ДХ. Параметри і а також кількість витків , довжина і діаметр соленоїда задаються як паспортні дані блоку соленоїда.

4. Блок-схема експериментальної установки показана на рис.6.

Блок живлення забезпечує регульований (регулятор Р) струм через соленоїд який вимірюється амперметром А, а також струм ДХ (І=4mA). Датчик Холла розміщений на рухомому штоці з міліметровою шкалою, нульова позначка якої фіксує положення ДХ в центрі соленоїда. Напруга на зондових контактах датчика Холла вимірюється цифровим вольтметром з точністю до третього знаку після коми.