Лабораторна робота № 5.3 Вивчення дифракції світла

Мета роботи: 1) перевірити метод зон Френеля у випадку дифракції світла на щілині; 2) визначити довжину світлової хвилі за допомогою дифракційної решітки.

Теоретичні відомості

(теорію до даної роботи див. також у конспекті лекцій, §§6.5-6.6)

А

мплітуда світлових коливань під час дифракції визначається за принципом Гюйгенса-Френеля. Взагалі це складна математична задача. Однак, у деяких простих і важливих практичних випадках наближене значення результуючої амплітуди може бути знайдено методом зон Френеля.

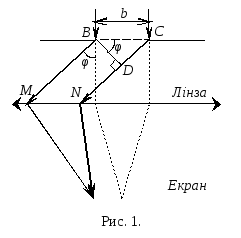
Нехай паралельний пучок монохроматичного світла падає нормально на довгу прямокутну щілину ВС шириною b (рис. 1).

Згідно принципу Гюйгенса-Френеля точки щілини є когерентними вторинними джерелами, коливання котрих відбуваються в одній фазі, бо площина щілини збігається з хвильовою поверхнею падаючої хвилі.

Хвиля, що дифрагує під кутом φ збирається лінзою на екрані. Щілину ВС можна розбити на зони Френеля у вигляді смуг таким чином щоб оптична різниця ходу променів CD містила ціле число k половин довжин хвилі . При цьому ширина кожної зони буде дорівнювати . Всі зони у певному напрямі випромінюють світло однаково. У випадку інтерференції світла від кожної пари сусідніх зон амплітуда результуючих коливань дорівнює нулю, оскільки ці зони спричиняють коливання з однаковими амплітудами, але протилежними фазами.

Якщо у щілині вкладається парне число (2k) зон Френеля, то амплітуда коливань у точці спостереження дорівнює нулю. Ця умова може бути записана у вигляді

, (1)

Під кутом φ, що задовольняє умові (1), спостерігається дифракційний мінімум.

Якщо у щілині вкладається непарне число зон Френеля (), то коливання від усіх зон, крім однієї, взаємно гасяться. У цьому випадку під певним кутом φ спостерігається дифракційний максимум, умова якого записується так

. (2)

При збільшенні кута φ число зон Френеля, що вкладаються у щілині, збільшується, а площа кожної зони зменшується. Це призводить до зменшення амплітуди (освітленості) зі збільшенням кута дифракції. У напрямку вся щілина світить як одна зона. Тому в центрі дифракційної картини спостерігається максимум найбільшої інтенсивності. Залежність інтенсивності від кута дифракції φ зображена на рисунку 3.

Дифракцію світла можна спостерігати не лише від однієї щілини, а й від системи багатьох вузьких щілин – дифракційної решітки. Для цього треба в установці, зображеній на рис. 1, замість щілини розмістити дифракційну решітку. В результаті спостерігається значно складніша дифракційна картина, котра для монохроматичного світла складається із чергування основних та побічних мінімумів і максимумів освітленості. Розрахунки показують, що положення k-того основного максимуму відповідає формулі:

, (3)

де d – період дифракційної решітки (відстань між двома сусідніми щілинами), φ – кут дифракції. За формулою (3) можна визначити довжину світлової хвилі.

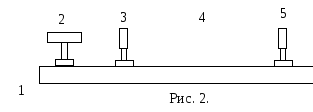
Опис експериментальної установки та виведення робочої формули

С

хема установки зображена на рис. 2. На цьому рисунку: 1 – оптична лава; 2 – газовий лазер; 3 – рейтер для установки щілини або дифракційної решітки; 4 – рейтер для установки збиральної лінзи з відомою фокусною відстанню; 5 – екран з затискачами, якими можна затискати аркуш паперу.

С

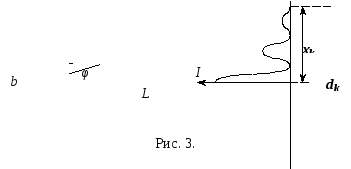
вітло від лазера падає на щілину, дифрагує і на екрані виникає дифракційна картина. Якщо ширина щілини значно менша ніж віддаль до екрану (рис. 3), то промені, що виходять від країв щілини і потрапляють у певну точку екрану, є практично паралельними (як у випадку, зображеному на рис. 1). За цих обставин умова (1) для щілини виконується досить точно.

Для утворення на екрані чіткої дифракційної картини від дифракційної решітки застосовується збиральна лінза, яка закріплюється в рейтері 4, а сам рейтер розміщується так, щоб екран знаходився у фокальній площині лінзи.

Завдання 1

Перевірка методу зон Френеля при дифракції світла на щілині

З рис. 3 видно, що

(4)

та

, (5)

де d_k – віддаль між двома мінімумами одного порядку, L – віддаль від щілини до екрану. З (1) та (5) отримаємо

. (6)

Із рівняння (6) випливає, що при виконанні умови (1) вираз

(7)

є прямо пропорційною функцією від k. Тому графіком залежності від k повинна буди пряма лінія, що проходить через початок координат. Саме це й перевіряється у лабораторній роботі.

Зауважимо, що у випадку функція має вигляд

. (8)