
Аналитическая геометрия на плоскости
Аналитическая геометрия – это раздел математики, изучающий геометрические образы алгебраическими методами.
Метод координат на плоскости
Метод координат заключается в установлении соответствия между точками прямой (плоскости, пространства) и их координатами – действительными числами при помощи системы координат.
Прямоугольная система координат
Прямоугольная система координат Oxy на плоскости задается двумя взаимно перпендикулярными прямыми, на каждой из которых выбрано положительное направление и задан единичный отрезок. Эти прямые называются осями координат. Одну из осей называют осью абсцисс и обозначают Ox, другую осью ординат (Oy).
Единичные
векторы осей
Ox
и Oy
обозначают соответственно
![]() и
и
![]() .
Если
.
Если
![]() - произвольная точка плоскости, то вектор
- произвольная точка плоскости, то вектор
![]() называется радиус-вектором
точки
называется радиус-вектором
точки
![]() .
.
Координатами
точки
![]() в
системе координат Oxy
называются координаты радиус-вектора
в
системе координат Oxy
называются координаты радиус-вектора
![]() .
.
Если
![]() ,
то координаты точки
,
то координаты точки
![]() записывают
так:
записывают
так:
![]() ;
при этом число
;
при этом число
![]() называется абсциссой
точки
называется абсциссой
точки
![]() ,
а число
,
а число
![]() -
ординатой
точки
-
ординатой
точки
![]() .
.
Координаты
точки полностью определяют ее положение
на плоскости: каждой паре чисел
![]() и
и
![]() соответствует единственная точка
соответствует единственная точка![]() плоскости,
и наоборот.
плоскости,
и наоборот.
Расстояние
между двумя точками
![]() и
и
![]() на
плоскости вычисляется по формуле
на
плоскости вычисляется по формуле
![]() (1)
(1)
Координаты
![]() точки
точки
![]() ,
делящей в заданном отношении
,
делящей в заданном отношении
![]() отрезок
отрезок
![]() ,
где
,
где
![]() и
и
![]() (
(![]() ),
находятся по формулам
),
находятся по формулам
![]() ,
,
![]() (2)
(2)
В
частности, при
![]() (точка
(точка
![]() делит
отрезок
делит
отрезок
![]() пополам),
получаются формулы координат середины
отрезка
пополам),
получаются формулы координат середины
отрезка
![]() ,
,
![]() (3)
(3)
Площадь
треугольника с вершинами
![]() вычисляется
по формуле
вычисляется
по формуле
![]() (4)
(4)
Полярная система координат
Полярная
система координат задается
точкой
![]() ,
называемой полюсом,
лучом
,
называемой полюсом,
лучом
![]() ,
называемым полярной
осью, и
единичным
вектором
,
называемым полярной
осью, и
единичным
вектором
![]() того же направления, что и луч
того же направления, что и луч
![]() .
.
П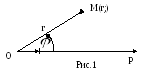 оложение
точки
оложение
точки
![]() на плоскости определяется двумя числами:
ее расстоянием
на плоскости определяется двумя числами:
ее расстоянием
![]() от полюса
от полюса
![]() и
углом
и
углом
![]() ,
образованным отрезком
,
образованным отрезком
![]() с
полярной осью (рис. 1) и отсчитываемым в
положительном направлении.
с
полярной осью (рис. 1) и отсчитываемым в
положительном направлении.
Числа
![]() и
и
![]() называются полярными
координатами точки
называются полярными
координатами точки
![]() :
:
![]() называют
полярным
радиусом,
называют
полярным
радиусом,
![]() - полярным
углом.
- полярным
углом.
Если
рассматривать значения
![]() в
промежутке
в
промежутке
![]() ,
а значения
,
а значения
![]() в
в
![]() (или
(или
![]() ),
то каждой точке плоскости (кроме
),
то каждой точке плоскости (кроме
![]() )
соответствует единственная пара чисел
)
соответствует единственная пара чисел
![]() и
и
![]() ,
и наоборот.
,
и наоборот.
Если
совместить полюс
![]() с началом координат системы
с началом координат системы
![]() ,
а полярную ось – с положительной полуосью
,
а полярную ось – с положительной полуосью
![]() (рис.2),
(рис.2),

то
связь между полярными и прямоугольными
координатами точки (кроме точки
![]() )
устанавливается формулами:
)
устанавливается формулами:
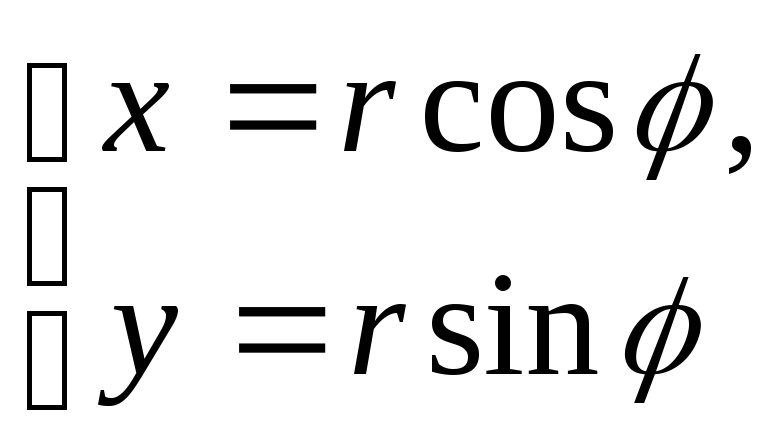 (5)
(5)
и
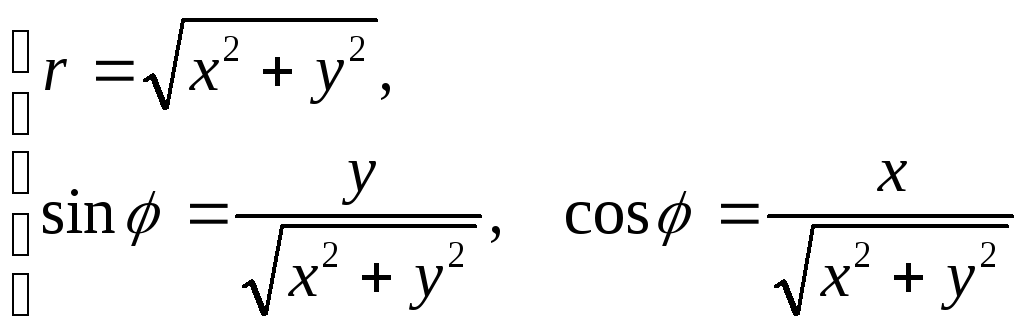 (6)
(6)
Откуда,
в частности
![]() ,
где
,
где
![]() .
.
Уравнение линии на плоскости
Уравнением
линии (кривой) на
плоскости
![]() называется
уравнение
называется
уравнение
![]() ,
которому удовлетворяют координаты
,
которому удовлетворяют координаты
![]() и
и
![]() каждой точки этой линии и только они.
Переменные
каждой точки этой линии и только они.
Переменные
![]() и
и
![]() в уравнении линии называются текущими
координатами точек линии.
в уравнении линии называются текущими
координатами точек линии.
Задача
о нахождении точек пересечения двух
линий, заданных уравнениями
![]() и
и
![]() ,
сводится к решению системы двух уравнений
с двумя неизвестными
,
сводится к решению системы двух уравнений
с двумя неизвестными
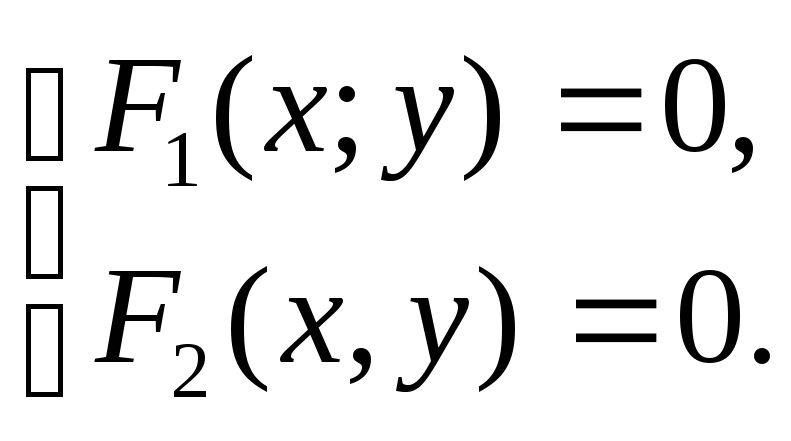 (7)
(7)
Аналогично
вводится понятие уравнения линии в
полярной системе координат:
![]() .
.
Линию
на плоскости можно рассматривать как
траекторию пути, пройденного точкой,
движущейся по какому-нибудь закону.
Если абсцисса точки
![]() изменяется по закону
изменяется по закону
![]() ,
а ордината – по закону
,
а ордината – по закону
![]() ,
где
,
где
![]() -
переменная, называемая параметром,
то уравнение линии записывается в виде
-
переменная, называемая параметром,
то уравнение линии записывается в виде
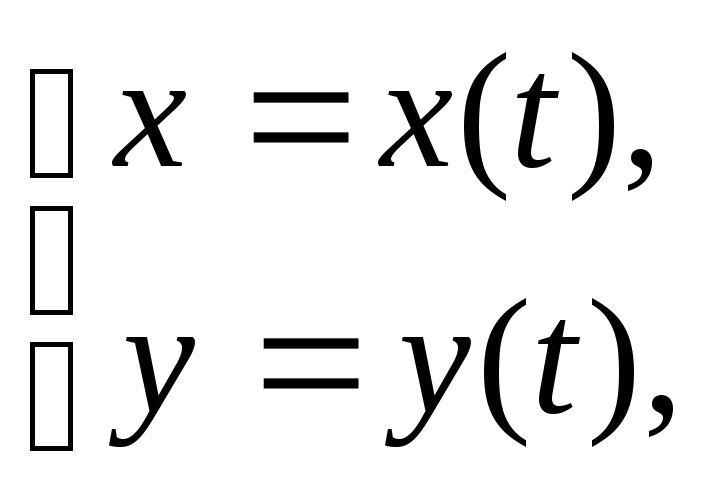
![]() (8)
(8)
Эти уравнения называются параметрическими уравнениями линии.
Линию
на плоскости можно задать векторным
уравнением
![]() ,
где
,
где
![]() -
скалярный параметр: при изменении
-
скалярный параметр: при изменении
![]() конец
вектора
конец
вектора
![]() описывают
некоторую линию, называемую
годографом
(рис.3). Параметрические уравнения
годографа
описывают
некоторую линию, называемую
годографом
(рис.3). Параметрические уравнения
годографа
![]() .
.

Рис.3
