РОЗДІЛ І

КВАНТОВО-МЕХАНІЧНІ ОСНОВИ ЛАЗЕРНОЇ ТЕХНІКИ

Лекція 1

Рівняння Шрединґера

1.1. Рівняння Шрединґера

В квантовій механіці поведінка мікрочастинки описується хвильовою функцією , яка є розв’язком рівняння Шрединґера

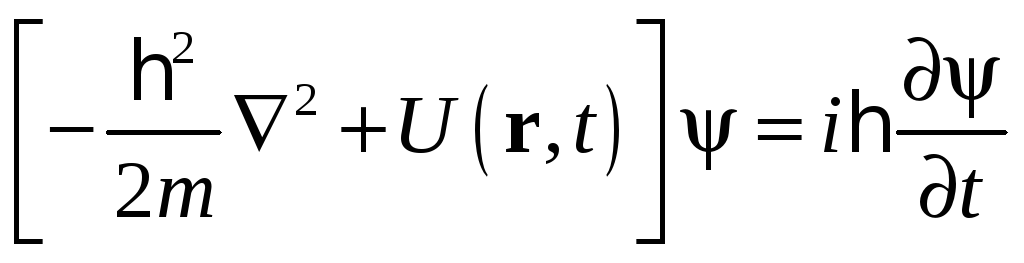, (1.1)

де – потенційна енергія, , – постійна Планка.

Імпульсу частинки в квантовій механіці відповідає диференціальний оператор ,тобто

(1.2)

то оператор в лівій частині (1.1) можна розглядати як квантовий аналог суми кінетичної і потенційної енергії частинки.

. (1.3)

Вимірявши в момент часу координати всіх частинок і підрахувавши відносне число частинок, що знаходяться в околі точки , отримаємо апріорну ймовірність виявлення частинки при вимірюванні всередині елементарного об’єму в момент часу В квантовій механіці густина ймовірності рівна:

. (1.4)

Перша умова, що випливає з статистичної інтерпретації полягає в тому, що повна ймовірність знаходження частинки де-небудь в просторі повинна бути скінченою і постійною:

(1.5)

імовірнісне трактування функції вимагає, щоб

(1.6)

1.2.Середні значення.

Середні значення радіус-вектора, що визначає положення частинки рівне:

(1.7)

Середнє значення оператора , що залежить від координат, імпульсу, енергії і часу:

. (1.8)

Це значення рівне середньому значенню фізичної величини. Всі оператори фізичних величин — ермітові оператори.

1.3.Ермітові оператори.

Оператор називається ермітово-спряженим оператору , якщо

(1.9)

де — дві любі скалярні функції.

Якщо , тобто то оператор називається ермітовим або самоспряженим.

1.4.Швидкість зміни середніх значень в часі.

.

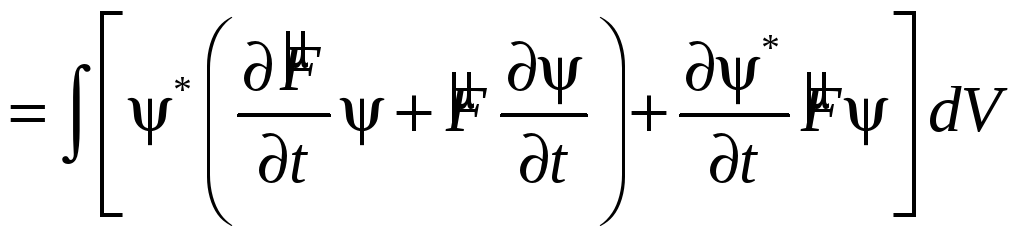Визначаючи оператор Намільтона як

, (1.11)

отримаємо згідно з (1.1): .

Виражаючи звідси похідні і , маємо:

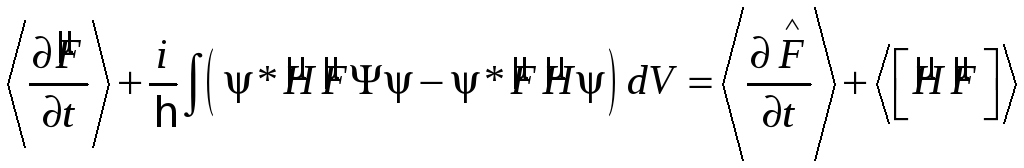. (1.12)

де використано як наслідок з ермітовості співвідношення:

— дужки Пуасона. (1.13)

1.5.Теорема Еренфеста.

Ця теорема стверджує, що класичні рівняння однієї частинки

(1.14)

справедливі, якщо всі вектори в (1.14) замінити на середні значення відповідних квантово-механічних операторів:

. (1.15)

1.6. Рівняння Шредінгера, що не містить часу.

Нехай розв’язок

(1.16)

представимо у вигляді Тоді рівняння (1.16) матиме вигляд:

. (1.17)

Якщо потенціальна енергія не залежить від часу явно, то рівняння (1.17) можна розділити на два рівняння з допомогою постійної розділення :

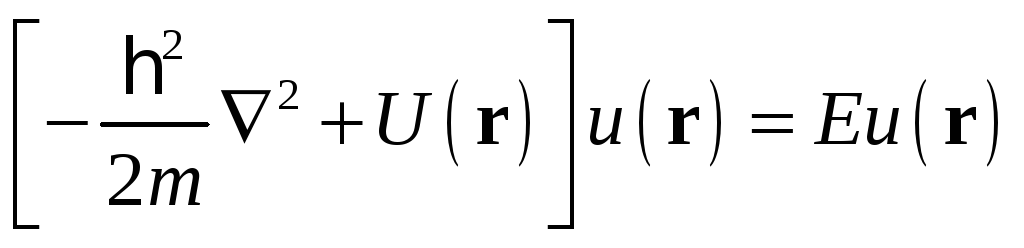, (1.19)

Розв’язок другого рівняння (1.19) має вигляд:

Перше рівняння (1.18) називають рівнянням Шрединґера, що не містить час. Його розв’язки називаються власними функціями оператора енергії. Власні значення оператора енергії утворюють множину (дискретну чи неперервну) допустимих значень і визначаються граничними умовами для або вимогами, що накладаються на в нескінченності . Допустимо, що система функцій є повна система.

Ортонормальність хвильових фукцій.

Любі дві функції з системи функцій , що відповідають різним значенням , ортогональні, тобто

коли Будемо виходити з рівняння Запишемо аналогічне рівняння для ; помножимо перше рівняння на , а друге на і віднімемо одне від другого. В результаті отримаємо:

Власні значення ермітового оператора дійсні, тому Проінтегруємо отримане рівняння по об’єму і скористаємося теоремою Гріна.

Оскільки вимагається виконання умови (1.5), інтеграл в лівій частині повинен обертатись в нуль, завдяки чому:

, коли . (1.20)

Нормування випливає з умови

і (1.21)

так що є частковим (пронормованим) розв’язком рівняння Шрединґера з часом.

Фізичний зміст .

Розглянемо випадок, коли хвильова функція представляє частковий розв’язок виду:

. (1.22)

Середнє значення оператора повної енергії , який був названий оператором Гамільтона або гамільтоніаном, рівне:

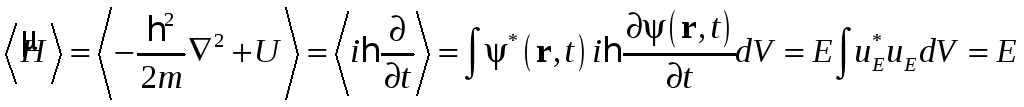. (1.21)

Таким чином , є середнім значенням оператора повної енергії , коли потенціальна функція явно не залежить від часу.

Деякі математичні властивості хвильових функцій.

Так як функції утворюють повну ортонормовану систему, їх можна використати для розкладу в ряд довільної функції :

і