1. Логічні операції та логічні змінні

Нехай множина . Елементи цієї множини називають логічними значеннями, а змінні, які можуть приймати логічні значення – логічними змінними.

Визначимо на множина логічні операції:

• 0-арні (нульмісні) операції – константи 0 та 1; (0), (1)

• 1-арні (одномісні) операції:

• повторення

(2)

• заперечення;

(3)

• 2-арні (двомісні) операції: кон’юнкцію, імплікацію, заперечення імплікації, суму за модулем 2, диз’юнкцію, стрілку Пірса, еквівалентності, штрих Шиффера.

• Кон’юнкція

; (4)

• Імплікація

; (5)

• Заперечення імплікації

; (6)

• Сума за модулем 2

; (7)

• Диз’юнкція

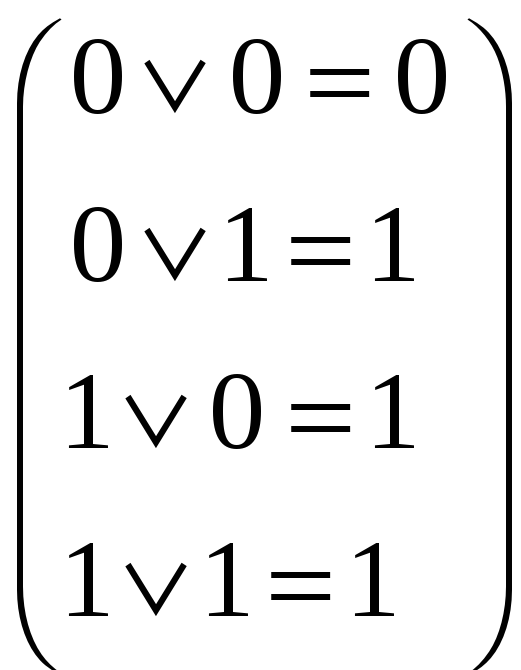; (8)

• Стрілка Пірса

; (9)

• Еквівалентність:

; (10)

• Штрих Шиффера:

; (11)

Вирази 0, 1, , , , , , , , , називаються логічними виразами (формулами). Вони є найпростішими логічними формулами. Більш складні формули можна одержати суперпозицією, при якій у вихідній формулі замість змінних підставляють інші вирази.

Приклад 1. Якщо в формулі взяти , , то одержимо більш складну формулу , яку також можна використати для одержання ще більш складної формули, наприклад, такої

.

2. Булеві функції

Функція називається булевою, якщо її значення і аргументи можуть приймати значення 0 і 1: і ().

Область визначення логічних функцій – множина ( разів). Елементи цієї множини – кортежі (n-ки) , які в математичній логіці називають словами і позначають рядком символів або стовпчиком із символів .

Кількість слів скінчена і дорівнює .

Приклад 1. При маємо два слова: 0, 1. При є чотири слова: 00, 01, 10, 11. При маємо вісім слів: 000, 111, 001, 101, 010, 011, 100, 110,

Кожному слову можна поставити у відповідність ціле число (номер слова)

. (1)

Приклад 2. Слову 010101 можна поставити у відповідність ціле число (номер)

.

Співставлення словам їх номерів дозволяє ввести на множині слів ідеальний строгий порядок: слово з меншим номером передує слову із більшим номером. Іншими словами, множину слів можна впорядкувати за зростанням їх номерів.

Приклад 3. При впорядкована множина слів така: 000 (відповідне число 0), 001(1), 010(2), 011(3), 100(4), 101(5), 110(6), 111(7).

Область значень будь-якої 3улевих функції – множина . Кількість 3улевих функцій скінчена і дорівнює . Кількість 3улевих функцій швидко зростає із збільшенням n. Так, при є 4 булеві функції однієї змінної, при 16 функцій двох змінних, при 256 функцій трьох змінних, а при більше 4-х трильйонів функцій п’яти змінних – всіх не перелічити.

Булевій функції n змінних можна поставити у відповідність число (номер функції)

, (2)

де – значення 3улевих функції на слові з номером 0, – на слові з номером 1 і т. д.

Співставлення функціям їх номерів дозволяє також ввести на множині функцій ідеальний строгий порядок: функція з меншим номером передує функції із більшим номер.

Номери повністю визначають булеві функції і дозволяють будувати таблиці істинності (таблиці істинності є одним із способів подання 3улевих функцій).

Приклад 4. Випишемо таблицю істинності функції , враховуючи, що .