Нахождение наибольшего и наименьшего значений в замкнутой области

Пусть и

Укажем правило нахождения и .

1. Находим стационарные точки функции в области , то есть решаем систему: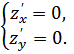

2. Вычисляем значение функции в этих точках.

3. Выбираем среди этих значений наибольшее и наименьшее.

Важно: исследовать характер стационарных точек не обязательно.

4. Провести исследование на экстремум на границе области , то есть на линии и найти .

5. Из пунктов 3 и 4 находим (путем сравнения) .

Об условном экстремуме. Функция и множитель Лагранжа (для )

Пусть точка – точка экстремума (, причем координаты точки удовлетворяет при этом и уравнению (дополнительному условию) связи:

def : точка - точка экстремума при условии (1), или:

точка - точка условного экстремума:

а) Необходимое условие существования условного экстремума.

Теорема 1. ] 1)

( непрерывные частные производные в ).

2) (точка не является особой точкой для ).

3) точка - точка условного экстремума, то есть (3).

[ для функции

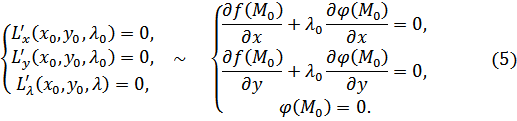
def. 1. Функция в (4) –функция Лагранжа.

2. в (4) – множитель Лагранжа.

Замечание: из (5) следует, что точка – стационарная точка функции Лагранжа .

б) Достаточные условия существования условного экстремума.

Теорема 2. ] 1) выполнены условия (5), то есть - стационарная точка функции из (4) (или точка - стационарная точка функции (при ).

2)

[ а) ] , то точка - точка условного __________ минимума для относительно условия (1):

б) ] , то точка - точка условного __________ максимума для относительно условия (1):

Пример1. Исследовать на условный экстремум

если

Решение:

1) Составим функцию Лагранжа :

2) Найдем

3) Решим систему:

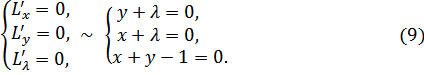
Имеем: (9) ~

Таким образом, получим стационарную точку для функции ~ точка при – точка, в которой может быть условный экстремум функции (6) при условии (7).

4. Найдем при :

Из (8):

5. Вычислим

6. Из (7) для

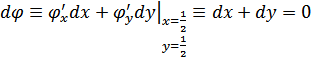, то есть

7. (12) подставим в (11): .

Вывод: точка при - точка условного максимума для (6) и (7) .

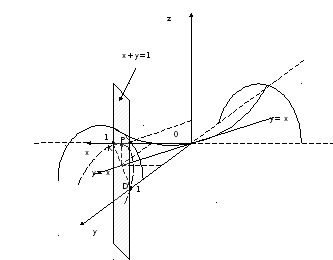
Рис. 1

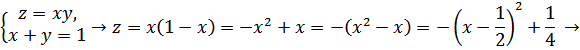
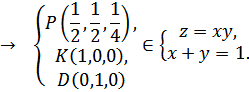
Парабола – сечение с плоскостью

Пример 2. Исследовать на экстремум среди тех точек , которые лежат на прямой

Решение. 1. Составим функцию Лагранжа

2.

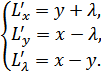
3. Решаем систему

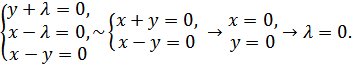
4. Из дополнительного условия при →

5.

6.

7.

В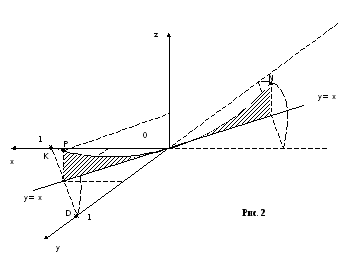ывод: точка - точка условного строго минимума для при .

40