Алгоритм графического метода решения злп

1. Построить прямые линии, уравнения которых получаем заменой в системе ограничений (2.1.2) знаков неравенств на знаки равенств.

2. Определить полуплоскости, соответствующие каждому ограничению задачи.

3. Найти многоугольник решений ЗЛП, учитывая, что .

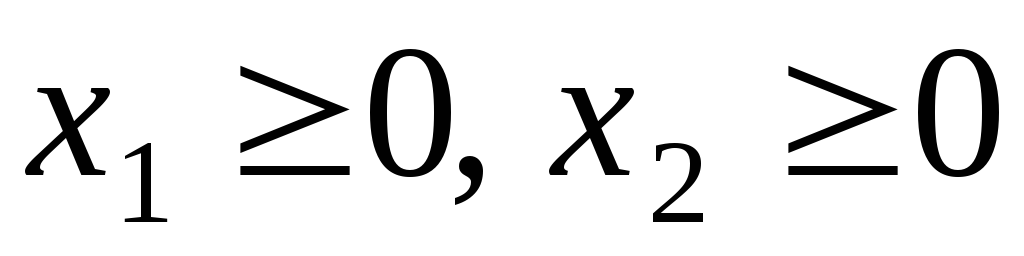4. Построить вектор направлений =(с₁,с₂), который указывает направление наибольшего возрастания целевой функции ЗЛП (2.1.1).

5. Построить прямую, которая проходит через область допустимых решений, перпендикулярно к вектору : . Это линия уровня.

6. Переместить прямую в направлении вектора в случае максимизации целевой функции; или в противоположном направлении в случае минимизации целевой функции, найти вершину многоугольника решений ЗЛП, в которой целевая функция достигает экстремального значения.

7. Определить координаты точки, в которой целевая функция достигает оптимальное значения, и вычислить экстремальное значение целевой функции в этой точке.

Реализацию графического метода решения ЗЛП рассмотрим на примерах.

Пример 2.2.1. Решить ЗЛП графическим методом:

(2.2.1)

max z = x₁ + 4x₂ (2.2.2)

Решение.

Для построения области допустимых решений, которая состоит из пересечения полуплоскостей, соответствующих каждому неравенству системы ограничений (2.2.1), запишем уравнения граничных прямых:

l₁: x₁ + 5x₂ = 5; l₂: x₁ + x₂ = 6; l₃: 7x₁ + x₂ = 7.

Замечание. Для удобства построения прямой линии, ее уравнение можно привести к виду в отрезках на осях

, (2.2.3)

где параметры а, b – длины отрезков, отсекаемых прямой на соответствующих осях Ох₁, Ох₂ .

Замечание. Если уравнение прямой линии имеет вид: Аx₁ + Вx₂ = 0, то она проходит через точку с координатами (0;0). Для ее построения следует выразить x₂ через x₁, и найти еще одну точку.

Для приведения уравнения прямой l₁ к виду (2.2.3.) разделим обе его части на 5: . Таким образом, прямая l₁ отсекает на оси Ох₁ 5 единиц, на оси Ох₂ – 1 единицу. Аналогично имеем для l₂: и l₃: .

Для определения полуплоскостей, которые отвечают ограничениям системы (2.2.1), в ограничения нужно подставить координаты какой-либо точки, не лежащей на граничной прямой. Если получим верное неравенство, то все точки из полуплоскости, в которой расположена выбранная точка, являются решениями данного неравенства. В противном случае выбирают другую полуплоскость.

Замечание. В качестве точки сравнения целесообразно выбирать, если это возможно, точку О(0,0).

Таким образом, первая и вторая искомые полуплоскости расположены в противоположную сторону от начала координат (0 – 5·0– 5; 7·0 + 07), а вторая – в сторону начала координат (0 + 0 6). Область допустимых решений на рисунке 1 заштрихована.

Замечание. В силу ограничений х₁ 0, х₂ 0, область допустимых решений ЗЛП всегда лежит в первой четверти координатной плоскости.

Рисунок 1 – Область допустимых решений

Для нахождения оптимального плана, который будет находиться в вершине многоугольника решений, нужно построить вектор направлений =(с₁,с₂), который указывает направление наибольшего возрастания целевой функции z = с₁х₁ + с₂х₂.

В данной задаче вектор направлений = (1, 4): он начинается в точке О(0,0) и заканчивается в точке N(1, 4).

Далее строим прямую, которая проходит через область допустимых решений, перпендикулярно к вектору , и называется линией уровня целевой функции. Передвигаем линию уровня в направлении вектора в случае максимизации целевой функции z и в направлении, противоположном , в случае минимизации z, до последнего пересечения с областью допустимых решений. В результате определяется точка или точки, где целевая функция достигает экстремального значения, или устанавливается неограниченность целевой функции z на множестве решений задачи.

Таким образом, точкой максимума целевой функции z является точка А пересечения прямых l₂ и l₃.

Для вычисления оптимального значения целевой функции z найдем координаты точки А – это точка пересечения прямых l₂ и l₃, решим систему уравнений:

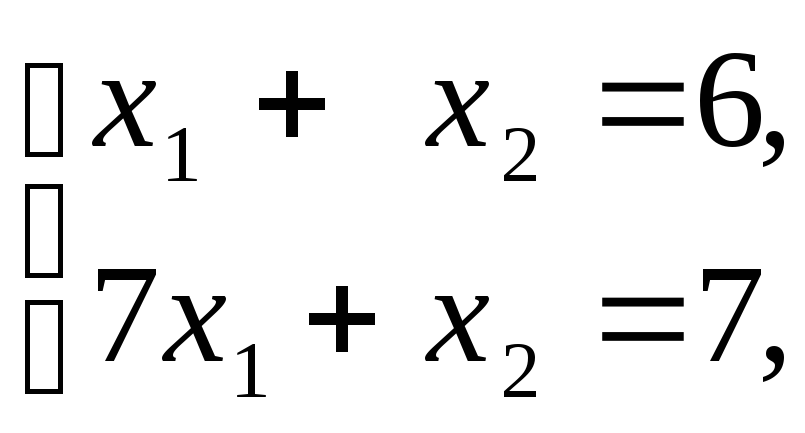
Таким образом, точка А имеет координаты x₁ =1/6, x₂ = 35/6.

Для вычисления оптимального значения целевой функции нужно подставить в нее координаты точки А.

Подставив координаты точки А в целевую функцию (2.4), получим

max z = 1/6 + 4·(35/6) = 47/2.

Пример 2.2.2. Построить на плоскости область допустимых решений системы линейных неравенств (2.2.4) и найти наибольшее и наименьшее значения целевой функции (2.2.5):

(2.2.4)

z = –2x₁ – x₂ (2.2.5)

Решение.

Для построения области допустимых решений, которая состоит из пересечения полуплоскостей, соответствующих каждому неравенству системы ограничений (2.2.4), запишем уравнения граничных прямых:

l₁: 4x₁ – x₂ = 0; l₂: x₁ + 3x₂ = 6; l₃: x₁ – 3x₂ = 6; l₄: x₂ = 1.

Прямая l₁ проходит через точку с координатами (0;0). Для ее построения выразим x₂ через x₁: x₂ = 4x₁. Найдем еще одну точку, через которую проходит прямая l₁ , например (1;4). Через точку с координатами (0;0) и точку с координатами (1;4) проведем прямую l₁ .

Для приведения уравнения прямой l₂ к виду в отрезках на осях (2.2.3.) разделим обе его части на 6: . Таким образом, прямая l₂ отсекает на оси Ох₁ 6 единиц, на оси Ох₂ 2 единицы. Аналогично имеем для l₃: и Прямая l₄ параллельна оси Ох₁ и проходит через точку с координатами (0;1) .

Для определения полуплоскостей, которые отвечают ограничениям системы (2.2.4) в ограничения нужно подставить координаты какой-либо точки, не лежащей на граничной прямой. В силу ограничений х₁ 0, х₂ 0, область допустимых решений ЗЛП лежит в первой четверти координатной плоскости.

Область допустимых решений на рисунке 2 заштрихована.

Рисунок 2 – Область допустимых решений

Построим вектор направлений = (–2,–1). Далее строим линию уровня, перпендикулярно к вектору .

Для нахождения наибольшего значения целевой функции передвигаем линию уровня в направлении вектора до последнего пересечения с областью допустимых решений. Таким образом, точкой максимума целевой функции z является точка А пересечения прямых l₁ и l₂.

Для вычисления оптимального значения целевой функции z найдем координаты точки А. Поскольку точка А – это точка пересечения прямых l₁ и l₂, то ее координаты удовлетворяют системе уравнений, составленной из уравнений соответствующих граничных прямых, которые пересекаются в оптимальной вершине:

Таким образом, точка А имеет координаты x₁ =6/13, x₂ = 24/13.

Подставив координаты точки А в целевую функцию (2.4), получим оптимальное значение целевой функции

max z = – 2·(6/13) – (24/13) = – 36/13.

Для нахождения наименьшего значения целевой функции передвигаем линию уровня в направлении противоположном вектору до последнего пересечения с областью допустимых решений. В этом случае целевая функция неограниченна в области допустимых решений, т.е. ЗЛП решений не имеет.

В результате решения ЗЛП возможны следующие случаи:

• Целевая функция достигает оптимального значения в единственной вершине многоугольника решений;

• Целевая функция достигает оптимального значения в любой точке ребра многоугольника решений (ЗЛП имеет альтернативные опорные планы);

• ЗЛП не имеет оптимальных планов;

• ЗЛП имеет оптимальный план в случае неограниченной многоугольника решений.