
- •Рецензенты:
- •Содержание
- •1. Программа курса Введение
- •Математические основы программирования
- •Общий вид задачи линейного программирования
- •Методы решения общей задачи линейного программирования
- •Двойственные задачи линейного программирования
- •Распределительные методы
- •Элементы нелинейного программирования
- •Элементы теории игр
- •Введение
- •Классификация задач математического программирования
- •2. Математическое программирование
- •2.1. Постановка задач линейного программирования
- •Алгоритм графического метода решения злп
- •2.3. Симплекс-метод решения задачи линейного программирования
- •Алгоритм симплекс-метода решения злп
- •Пример 2.3.1. Решить злп (2.2.1), (2.2.5) симплекс-методом.
- •Критерий оптимальности опорного плана:
- •Переход к следующей симплекс-таблице осуществляют по правилам:
- •2.4. Двойственная задача линейного программирования
- •2.5. Элементы теории матричных игр
- •Алгоритм принципа максимина (минимакса)
- •Решение. Эта матричная игра имеет размерность (3х4), т.Е. Игрок а имеет три стратегии, а игрок в – четыре. Запишем ее в нормальной форме.
- •Последовательность действий при решении игры
- •2.6. Транспортная задача. Метод потенциалов
- •Алгоритм метода потенциалов состоит из следующих этапов:
- •Критерий оптимальности плана перевозок
- •2.7. Задача о назначениях
- •Алгоритм метода Фогеля
- •Алгоритм венгерского метода решения задачи о назначениях
- •2.8. Дробно-линейное программирование
- •Правила решения задачи дробно-линейного программирования графическим методом
- •2.9. Целочисленное программирование
- •2.10. Параметрическое программирование
- •Алгоритм решения задачи параметрического программирования
- •3. Задания для самостоятельной работы
2.10. Параметрическое программирование
Экономические задачи, в которых в
линейную целевую функцию или правую
часть системы ограничений входит
параметр, изучает параметрическое
программирование. Например, если
эффективность или доход зависят от
сезонных колебаний, тогда критерий
оптимальности должен эту зависимость
отображать. Если продукция, которая
изготовлена предприятием, должна
некоторое время сохраняться, то ее
стоимость состоит из двух частей:
постоянной – это стоимость продукции
на момент изготовления – и переменной
части, которая зависит от срока хранения,
причем эта зависимость, как правило,
линейная. Целевая функция задачи
оптимального планирования такого
производства будет иметь коэффициенты,
которые линейно зависят от параметра
t![]() (от времени).
(от времени).
Метод решения задач параметрического программирования состоит в следующем:
-
полагают, что параметр t равен меньшему значению из промежутка
 ,
т.е. t = а,
тогда все коэффициенты целевой функции
будут постоянными; решают задачу
линейного программирования для этого
случая, т.е. находят вершину, в которой
достигнут экстремум;
,
т.е. t = а,
тогда все коэффициенты целевой функции
будут постоянными; решают задачу
линейного программирования для этого
случая, т.е. находят вершину, в которой
достигнут экстремум; -
определяют все значения параметра t, для которых оптимальное решение сохраняется, то есть для которых экстремальное значение достигается в одной и той же точке. Найденные значения исключают из интервала изменения параметра
 ;
для оставшегося интервала вновь решают
задачу до тех пор, пока не будут найдены
решения для всех значений t.
;
для оставшегося интервала вновь решают
задачу до тех пор, пока не будут найдены
решения для всех значений t.
Алгоритм решения задачи параметрического программирования
1. Целевую функцию устремить к минимуму; систему ограничений привести к каноническому виду, вводя дополнительные переменные; ввести искусственные переменные, если нужно.
2. Присвоить параметру t
наименьшее значение из отрезка
![]() .
Соответственно с этим конкретизируют
целевую функцию.
.
Соответственно с этим конкретизируют
целевую функцию.
3. Строят первую симплексную таблицу в соответствии с правилами.
4. Дополнить первую симплекс-таблицу двумя строками: р –строкой и q-строкой.
-
В р-строке нужно записать с противоположным знаком коэффициенты целевой функции, не связанные с параметром t.
-
В q-строке нужно записать с противоположным знаком коэффициенты целевой функции, связанные с параметром t.
5. Проводить нужно расчеты всех элементов таблицы в соответствии с правилами симплексного метода, проверяя оптимальность на основе М-строки, а потом z-строки.
6. Выписать оптимальное решение, если критерий эффективности выполнился После этого z-строка во внимание не берется.
7. Находят для параметра t
частичный интервал постоянства решения,
рассматривая такие случаи (![]() – начало интервала,
– начало интервала,
![]() – конец интервала):
– конец интервала):
а) все
![]() ,
то частичный интервал постоянства
решения определяется по формулам
(2.10.1):
,
то частичный интервал постоянства
решения определяется по формулам
(2.10.1):
![]() ,
(2.10.1)
,
(2.10.1)
б) все
![]() ,
то частичный интервал постоянства
решения определяется по формулам
(2.10.2):
,
то частичный интервал постоянства
решения определяется по формулам
(2.10.2):
![]() ,
(2.10.2)
,
(2.10.2)
в)
![]() принимают как положительные, так и
отрицательные значения – в этом
случае частичный интервал постоянства
решения определяется по формулам
(2.10.3):
принимают как положительные, так и
отрицательные значения – в этом
случае частичный интервал постоянства
решения определяется по формулам
(2.10.3):
|
|
(2.10.3) |
8. Если полученный интервал не
охватывает отрезок
![]() ,
то необходимо продолжить поиск и
найти решения для других значений
параметра t.
,
то необходимо продолжить поиск и
найти решения для других значений
параметра t.
9. Выбрать в качестве разрешающего
столбца тот столбец, в котором получено
значение
![]() .
Затем выполнить симплекс-преобразование
и определить новый частичный интервал
для нового решения. Эту процедуру
повторяют до тех пор, пока будет
пройден весь отрезок
.
Затем выполнить симплекс-преобразование
и определить новый частичный интервал
для нового решения. Эту процедуру
повторяют до тех пор, пока будет
пройден весь отрезок
![]() .
.
Пример 2.10.1. Решить задачу параметрического программирования
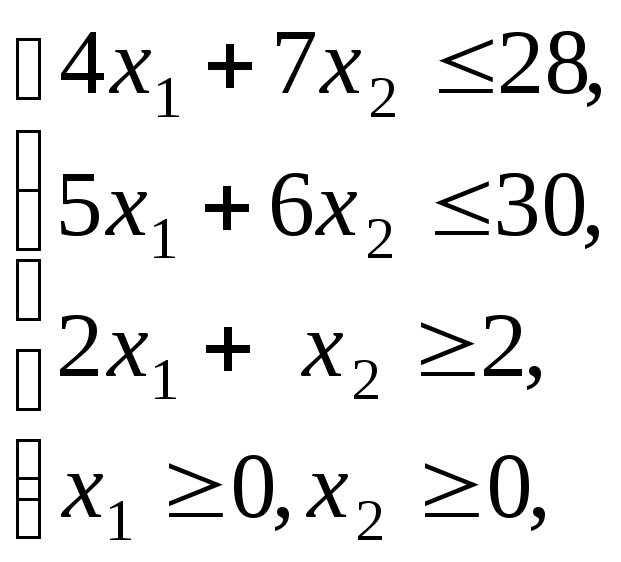 (2.10.4)
(2.10.4)
![]() ,
,
![]() (2.10.5)
(2.10.5)
Решение. Приведем задачу к каноническому виду

![]() ,
,
где х1, х2 – основные переменные, х3, х4, х5 – дополнительные переменные; х6 – искусственная переменная.
Присвоим параметру t
наименьшее значение из интервала
![]() ,
и конкретизируем целевую функцию: при
t = 0 имеем
,
и конкретизируем целевую функцию: при
t = 0 имеем
![]() .
.
Первая симплексная таблица с дополнительными строками будет иметь вид:
Таблица 2.10.1
Первая симплексная таблица
-
Б
С

1
-2
0
0
0
М
р1
р2
р3
р4
р5
р6
С.0.
р3
0
28
4
7
1
0
0
0
28/7=4
р4
0
30
5
6
0
1
0
0
30/6=5
р6
М
2
2
1
0
0
-1
1
2/1=2
z - строка
0
-1
2
0
0
0
0
М-строка
2
2
1
0
0
0
0
р-строка
0
-1
2
0
0
0
0
q-строка
0
1
-1
0
0
0
0
Для решения, соответствующего этой симплексной таблице, критерий оптимальности не выполняется. По правилам перехода к следующей симплексной таблице, получим вторую симплексную таблицу.
Таблица 2.10.2
Вторая симплексная таблица
-
Б
С

1
-2
0
0
0
р1
р2
р3
р4
р5
С.0.
р3
0
14
-10
0
1
0
7
14/7=2
р4
0
18
7
0
0
1
6
18/6=3
р2
-2
2
-2
1
0
0
-1
-
z - строка
-4
-5
0
0
0
2
р-строка
-4
-5
0
0
0
2
q-строка
2
3
0
0
0
1
Для решения, соответствующего этой симплексной таблице, критерий оптимальности не выполняется. По правилам перехода к следующей симплексной таблице, получим третью симплексную таблицу.
Таблица 2.10.3
Третья симплексная таблица
-
Б
С

1
-2
0
0
0
р1
р2
р3
р4
р5
С.О.
р5
0
2
-10/7
0
1/7
0
1
р4
0
6
11/7
0
-6
1
0
6/(11/7)=42/11
р2
-2
4
4/7
1
1/7
0
0
4/(4/7)=7
z - строка
-8
-15/7
0
-2/7
0
0
р-строка
-8
-15/7
0
-2/7
0
0
q-строка
4
11/7
0
1/7
0
0
Третьей симплексной таблице соответствует решение
![]() ,
,
которое является оптимальным. Оно будет сохраняться для определенных значений параметра t. Поскольку все qi положительны, то имеем случай а) пункта 7 и по формуле (2.10.1):
![]()
Значит,
точка А
с координатами
![]() обеспечивает минимум целевой функции
для параметра t
обеспечивает минимум целевой функции
для параметра t![]() .
Этот интервал не покрывает отрезок
.
Этот интервал не покрывает отрезок
![]() ,
поэтому решение задачи следует продолжить.
В качестве разрешающего столбца нужно
выбрать столбец р1,
поскольку в нем получено значение
,
поэтому решение задачи следует продолжить.
В качестве разрешающего столбца нужно
выбрать столбец р1,
поскольку в нем получено значение
![]() .
Все расчеты выполняем в соответствии
с правилами симплексного метода.
.
Все расчеты выполняем в соответствии
с правилами симплексного метода.
Таблица 2.10.4
Четвертая симплексная таблица
-
Б
С

1
-2
0
0
0
р1
р2
р3
р4
р5
р5
0
82/77
0
0
-7/11
10/11
1
р1
1
42/11
1
0
-6/11
7/11
0
р2
-2
20/11
0
1
5/11
-4/11
0
z - строка
2/11
0
0
-16/11
15/11
0
р-строка
2/11
0
0
-16/11
15/11
0
q-строка
-2
0
0
1
-1
0
Четвертой симплексной таблице соответствует решение
![]() ,
,
которое будет обеспечивать оптимальность целевой функции для значений параметра t, которые находятся на основе случай в) пункта 7 по формуле (2.10.3), поскольку qi как положительны так и отрицательны:
![]() ,
,
![]() .
.
Значит,
точка В
с координатами
![]() обеспечивает минимум целевой функции
для параметра t
обеспечивает минимум целевой функции
для параметра t![]() .
Этот интервал также не покрывает отрезок
.
Этот интервал также не покрывает отрезок
![]() ,
поэтому решение задачи следует продолжить.
В качестве разрешающего столбца нужно
выбрать столбец р3,
поскольку в нем получено значение
,
поэтому решение задачи следует продолжить.
В качестве разрешающего столбца нужно
выбрать столбец р3,
поскольку в нем получено значение
![]() .
Все расчеты выполняем в соответствии
с правилами симплексного метода.
.
Все расчеты выполняем в соответствии
с правилами симплексного метода.
Таблица 2.10.5
Пятая симплексная таблица
-
Б
С

1
-2
0
0
0
р1
р2
р3
р4
р5
р5
0
278/77
0
7/5
0
2/5
1
р1
1
6
1
6/5
0
1/5
0
р3
0
4
0
11/5
1
-4/5
0
z - строка
6
0
16/5
0
1/5
0
р-строка
6
0
16/5
0
1/5
0
q-строка
-6
0
-11/5
0
-1/5
0
Пятой симплексной таблице соответствует решение
![]() ,
,
которое будет обеспечивать оптимальность целевой функции для значений параметра t, которые находятся на основе случая б) пункта 7 по формуле (2.10.2), поскольку все qi отрицательны:
![]() ,
,
![]() .
.
Значит,
точка С
с координатами
![]() обеспечивает минимум целевой функции
для параметра t
обеспечивает минимум целевой функции
для параметра t![]() .
Этот интервал покрыл отрезок
.
Этот интервал покрыл отрезок
![]() ,
поэтому решение задачи следует закончить.
,
поэтому решение задачи следует закончить.
Таким образом,
если t![]() ,
то целевая функция достигнет минимума
при
,
то целевая функция достигнет минимума
при
![]() ;
если t
;
если t![]() ,
то целевая функция достигнет минимума
при
,
то целевая функция достигнет минимума
при
![]() ;
если t
;
если t![]() ,
то целевая функция достигнет минимума
при
,
то целевая функция достигнет минимума
при
![]() .
.
Дадим геометрическую интерпретацию полученного решения задачи.
Область допустимых решений, соответствующая системе ограничений (2.9.1), изображена на рисунке 5. Она представляет собой пятиугольник АВСDЕ.

Рисунок 5 – Область допустимых решений
Вектор-градиет направления возрастания будет зависеть от значения параметра t.
-
При t = 0 имеем
 ,
т.е.
,
т.е.
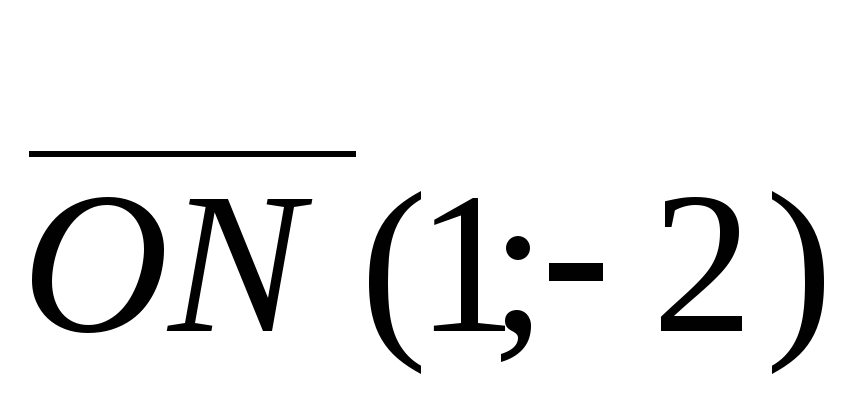 ,
при t
=
,
при t
=
 имеем
имеем
 ,
т.е.
,
т.е.
 ,
т.е. если t
,
т.е. если t ,
то целевая функция z
достигнет минимума в точке А
(0; 4).
,
то целевая функция z
достигнет минимума в точке А
(0; 4).
-
При t =
 имеем
имеем
 ,
т.е.
,
т.е.
 ,
т.е. если t
,
т.е. если t ,
то целевая функция z
достигнет минимума в точке В
,
то целевая функция z
достигнет минимума в точке В .
.
-
При t = 6 имеем
 ,
т.е.
,
т.е.
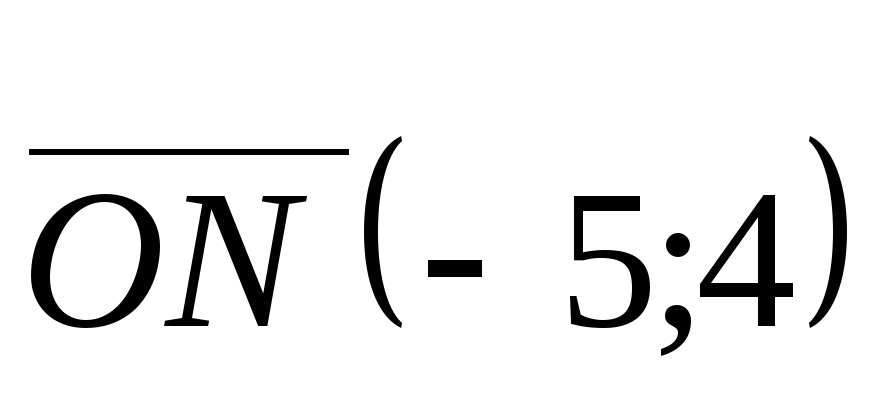 ,
т.е. если t
,
т.е. если t ,
то целевая функция z
достигнет минимума в
точке С
(6; 0).
,
то целевая функция z
достигнет минимума в
точке С
(6; 0).
