2.8. Дробно-линейное программирование
Если в задаче с линейными ограничениями задана дробно-линейная целевая функция, то такая задача может быть преобразована к традиционному виду путем алгебраических преобразований. Преобразованная задача может быть разрешена симплексным методом, а найденное решение трансформировано в решение исходной задачи дробно-линейного программирования. Все этапы алгоритма проиллюстрируем на конкретном примере.
Пример 2.8.1. Решить задачу дробно-линейного программирования
(2.8.1)
(2.8.2)
Решение. Систему ограничений (2.8.1) приведем к каноническому виду:
(2.8.3)
где х1, х2 – основные переменные, х3, х4, х5 – дополнительные переменные; х6, х7 – искусственные переменные.
Знаменатель целевой функции (2.8.2)
обозначим через
,
тогда
или
(2.8.4)
Равенство (2.8.4) является новым дополнительным ограничением, которое нужно ввести в систему (2.8.3).
В этом случае целевая функция (2.8.2) приобретет вид:
.
Все
ограничения системы (2.8.3) умножим на
и введем в нее дополнительное ограничение
(2.8.4), получим систему (2.8.5):
(2.8.5)
Введем следующие обозначения (2.8.6)
,
,
,
,
,
,
.
(2.8.6)
С
учетом обозначений (2.8.6), нужно упорядочить
систему (2.8.5), перенося из правой части
слагаемые, содержащие
.
Кроме того, для образование единичного
базиса, в дополнительное ограничение
(2.8.4), нужно ввести искусственную
переменную со следующим номером. В
данном случае введем искусственную
переменную
.
В результате указанных преобразований
получим следующую задачу:
(2.8.7)
.
Найти
решение полученной задачи (2.8.7) можно
симплекс-методом. Поскольку индексы
векторов должны соответствовать индексам
переменных (
,
,
и т.д.), вектор свободных членов обозначим
.
Векторы коэффициентов при неизвестных и вектор свободных членов таковы:
,
,
,
,
,
,
,
,
,
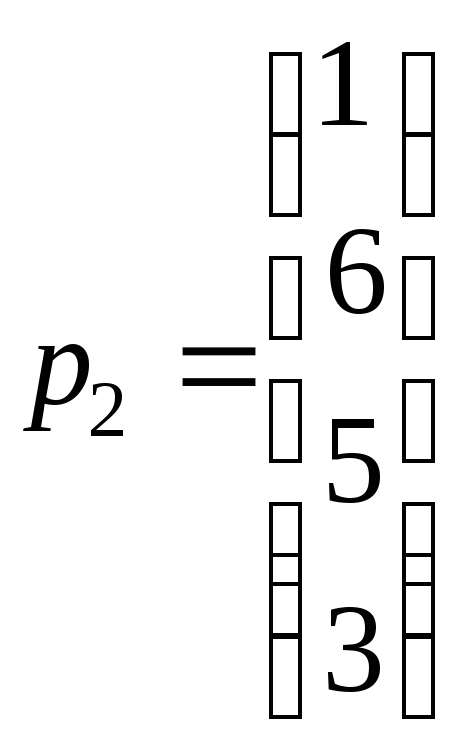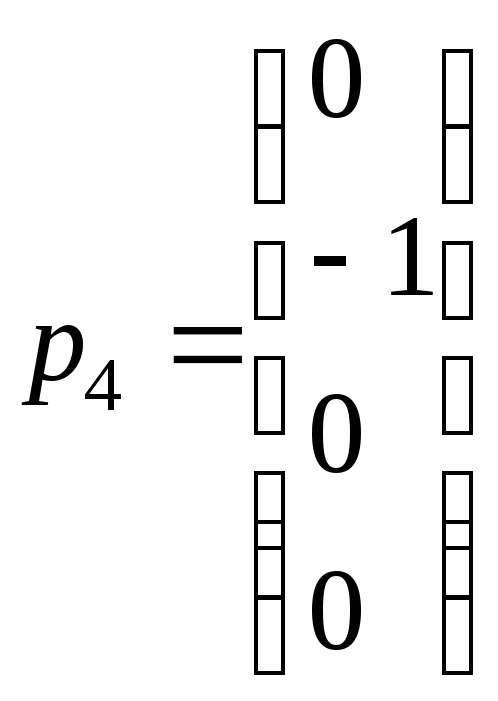Первая симплексная таблица будет иметь вид:
Таблица 2.8.1
Первая симплексная таблица
|
Б |
С |
|
0 |
2 |
5 |
0 |
0 |
0 |
М |
М |
М |
С.О. |
|
р0 |
р1 |
р2 |
р3 |
р4 |
р5 |
р6 |
р7 |
р8 |
||||
|
р6 |
М |
0 |
-5 |
5 |
1 |
-1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
р7 |
М |
0 |
-6 |
1 |
6 |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
|
р5 |
0 |
0 |
-20 |
4 |
5 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
р8 |
М |
1 |
0 |
4 |
3 |
0 |
0 |
0 |
0 |
0 |
1 |
1/4 |
|
z - строка |
0 |
0 |
-2 |
-5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
М-строка |
1 |
-11 |
10 |
10 |
-1 |
-1 |
0 |
0 |
0 |
0 |
|
|
Этой симплексной таблице соответствует следующее решение:
,
,
,
,
,
,
,
,
.
Это решение не является оптимальным. При выборе разрешающей строки нужно выбрать ту, которая соответствует наибольшему элементу разрешающего столбца. В данном случае выберем строку р6 и генеральный элемент равен 5. Вторая симплексная таблица будет иметь вид:
Таблица 2.8.2
Вторая симплексная таблица
-
Б
С
0
2
5
0
0
0
М
М
С.О.
р0
р1
р2
р3
р4
р5
р7
р8
р1
2
0
-1
1
1/5
-1/5
0
0
0
0
0
р7
М
0
-5
0
29/5
1/5
-1
0
1
0
0
р5
0
0
-16
0
21/5
4/5
0
1
0
0
0
р8
М
1
4
0
11/5
4/5
0
0
0
1
5/11
z - строка
0
-2
0
-23/5
-2/5
0
0
0
0
М-строка
1
-1
0
8
1
-1
0
0
0
Этой симплексной таблице соответствует следующее решение:
,
,
,
,
,
,
,
,
.
Это решение не является оптимальным. Переход к следующей симплексной таблице производим по правилам симплекс-метода и с учетом комментария по выбору разрешающей строки. Третья симплексная таблица будет иметь вид:
Таблица 2.8.3
Третья симплексная таблица
-
Б
С
0
2
5
0
0
0
М
С.О.
р0
р1
р2
р3
р4
р5
р8
р1
2
0
-24/29
1
0
-1/29
1/29
0
0
0
р2
5
0
-25/29
0
1
1/29
-5/29
0
0
0
р5
0
0
-359/29
0
0
19/29
21/29
1
0
0
р8
М
1
171/29
0
0
21/29
11/29
0
1
29/171
z - строка
0
-173/29
0
0
-7/29
-23/29
0
0
М-строка
1
171/29
0
0
21/29
11/29
0
0
Этой симплексной таблице соответствует следующее решение:
,
,
,
,
,
,
,
,
.
Это решение также не является оптимальным. Переходим к четвертой симплекс таблице:
Таблица 2.8.4
Четвертая симплексная таблица
-
Б
С
0
2
5
0
0
0
С.О.
р0
р1
р2
р3
р4
р5
р1
2
24/171
0
1
0
-18/171
15/171
0
-
р2
5
25/171
0
0
1
24/171
-20/171
0
25/24
р5
0
359/171
0
0
0
372/171
260/171
1
359/372
р0
0
29/171
1
0
0
21/171
11/171
0
29/21
z - строка
173/171
0
0
0
84/171
-70/171
0
Этой симплекс-таблице соответствует следующее решение:
,
,
,
,
,
.
Это решение также не является оптимальным. Переходим к пятой симплекс таблице:
Таблица 2.8.5
Пятая симплексная таблица
-
Б
С
0
2
5
0
0
0
р0
р1
р2
р3
р4
р5
р1
2
90/372
0
1
0
0
р2
5
4/372
0
0
1
0
р3
0
359/372
0
0
0
1
р0
0
19/372
1
0
0
0
z - строка
200/372
0
0
0
0
-280/372
-84/372
Этой симплексной таблице соответствует следующее решение:
,
,
,
,
.
Найдем значения исходных переменных, используя формулы (2.8.6):
,
.
Таким образом, решение данной задачи дробно-линейного программирования имеет вид:
,
,
.
Задачу дробно-линейного программирования с двумя переменными можно решать графическим методом.