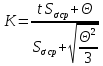Вопросы к защите работы

1. Причина возникновения погрешностей при определении измеряемых величин по показаниям приборов, включённых через измерительные трансформаторы, с учётом номинальных коэффициентов трансформации.

2. Режимы работы измерительных трансформаторов тока и напряжения.

3. Цель и методы разметки зажимов измерительных трансформаторов тока и напряжения.

4. Влияние изменения сопротивления нагрузки вторичной цепи трансформатора напряжения на его погрешности.

5. Способы уменьшения погрешностей трансформаторов тока.

6. Вывод выражения для определения результата измерения мощности электродинамическим ваттметром, включённым через измерительные трансформаторы тока и напряжения.

7. Почему при измерениях мощности в цепях с малым угловые погрешности измерительных трансформаторов могут увеличить погрешности измерения?

8. Определить цену деления амперметра и вольтметра, включённых через измерительные трансформаторы, если цена деления самих приборов равна C_А= 0,05 А/дел, C_V = 1 В/дел, а коэффициенты трансформации ; .

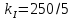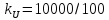9. Причина, по которой не допускается размыкать вторичную обмотку трансформатора тока под нагрузкой. Причина заземления одного из её концов.

Лабораторная работа № 5

Расчет погрешностей при измерениях

косвенным методом

Цель работы

Ознакомление с практикой расчета погрешностей при измерениях косвенным методом.

Основные теоретические положения

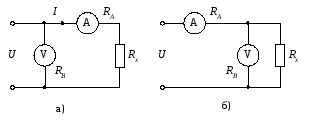
При косвенных измерениях, например, сопротивления методом амперметра и вольтметра обычно используют две схемы, рис. 5.1,5.2.

Метод амперметра и вольтметра является наиболее легко осуществимым, а потому довольно распространенным.

В зависимости от соотношения сопротивлений измерительного прибора и измеряемого объекта 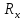применяют так называемые схемы правильного включения амперметра (рис. 5.1) и вольтметра (рис. 5.2).

Рис. 1. Схема правильного включения амперметра.	Рис. 2. Схема правильного включения вольтметра.

При измерениях всегда возникают погрешности. Истинное значение измеряемой величины заключено в некотором интервале, определяемом величиной абсолютной суммарной погрешности результата измерения :

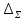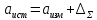
Абсолютная суммарная погрешность измерения 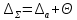имеет две составляющие, одна из которых - 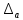(случайная погрешность), а вторая 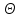- (неисключенная систематическая погрешность). Причем, каждая из этих составляющих сама является суммой, т.е. складывается, например, из нескольких систематических погрешностей или нескольких случайных погрешностей.

Обычно систематические погрешности имеют весьма явную причину. Например, инструментальная погрешность, погрешность метода, погрешность от влияющих величин и др. Погрешность метода (имеет место в схемах рис.5.1 и рис.5.2), как правило, может быть исправлена на предварительном этапе расчета.

Если производятся косвенные измерения (два измерительных прибора в данной лабораторной работе), то тогда результат измерения 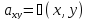. Суммарная неисключенная инструментальная погрешность в этом случае вычисляется по формуле:

𝛩

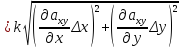
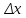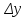где и – абсолютные приборные погрешности вольтметра и амперметра соответственно,

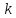– коэффициент, определяемый принятой доверительной вероятностью (при p=0.95, 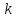=1.1).

Величину отдельной случайной погрешности, в отличие от систематической, вычислить невозможно, хотя эти погрешности реально существуют и искажают результат измерения. Для учета случайных погрешностей выполняют многократные измерения одной и той же величины.

Вероятность того, что это среднее арифметическое будет истинным значением, равна единице при проведении бесконечно большого числа измерений.

Так как реально ограничиваются 10-15 измерениями, случайные погрешности можно довольно точно описать, пользуясь нормальным (гауссовым) распределением. Обработку результатов измерений проводят по следующему алгоритму:

1. 1. Находим среднее арифметическое результатов ряда измерений:

2. 

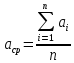
3. 2. Находим остаточные суммы:

4. 

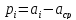
5. 3. Сумма этих остаточных сумм 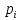должна быть минимальной, т.е.:

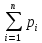6. ≈ 0

Если это не так, то в ряду измерений имеется промах, т.е. результат, который получен ошибочно. Его численное значение заметно отличается от значений других результатов. Делаем анализ ряда измерений и отмечаем подозрительные результаты.

7. 4. Находим сумму квадратов остаточных сумм .

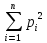8. 5. Находим оценку среднеквадратичного отклонения (СКО) ряда измерений.

9. 

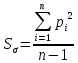
10. 6. Проверяем остаточные суммы на выполнение условия:

11. -

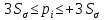
Если имеется результат измерения, для которого это условие не выполняется, то это – промах. Его нужно исключить и повторить расчет (п.1-6).

12. 7. Вычисляем оценку СКО 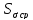среднего арифметического ряда измерений

13. 

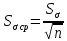
Так как 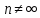, вводим поправочный коэффициент, позволяющий получить значение погрешности результата измерений более точно, чем погрешность, численно равная 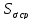. Такому случаю при нормальном распределении результатов соответствует распределение Стьюдента. Используя коэффициент Стьюдента, можно определить погрешность результата для каждого конкретного ряда измерений, то есть найти наиболее вероятную погрешность окончательного результата ряда измерений :

1. ,

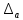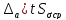2. где 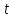– коэффициент Стьюдента.

Коэффициент Стьюдента находится по таблицам в зависимости от заданной вероятности результатов измерений и числа измерений в ряду.

Поскольку в любом измерении может присутствовать и систематическая погрешность и случайная погрешность, их необходимо суммировать.

Если в ряду измерений наблюдаются случайная и систематическая погрешности, то рассматривается 3 случая:

1. Если 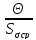≤ 0.8, то систематической погрешностью можно пренебречь и считать, что .

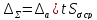2. Если 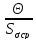≥ 8, то случайной погрешностью можно пренебречь и считать, что

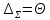
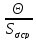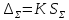3. Если 0.8 < < 8, то , где

,
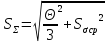