2.4.2.Енергія сигналу, визначена через його значення в окремих точках.

(12)

якщо частота необмежено росте, тобто тоді функція відліків перетворюється в функцію, ,і Ряд Котельникова буде:

dt,

що очевидно. Ми отримали інтеграл Дюамеля!

Теорема Котельникова лежить в основі дискретної, числової передачі інформації при імпульсній модуляції. Згідно даної теореми необхідна частота слідування імпульсів (тактова частота) повинна визначатись із умови , де - верхня границя спектру повідомлення.

Цікаво відмітити, що теорема Котельникова говорить про спектри сигналу, що починаються в точці f= 0 і закінчуються в , . Якщо ж , тобто ширина спектра , то теорему Котельникова необхідно дещо перефразувати. Щоб відновити функцію необхідно і достатньо передавати сигнал з частотою але не лише амплітудні а і фазові значення функції в точках дискретизації . Тобто необхідно передавати та . Оскільки сигнал відомий (стартова інформація) то це дійсно можна зробити.

2.4.3.Особливості застосування теореми Котельникова, Фізична суть і ще раз.

Теорема Котельникова стверджує, що коли необхідно передати сигнал з обмеженим спектром F то достатньо передати його значення в точках відліку . На приймальному кінці існує можливість повного відновлення у випадку відсутності шуму.

Для практичного застосування теореми Котельникова необхідно вказати реальні пристрої відновлення по значенню . Спосіб дискретного зняття інформації відносно простий. Його здійснюють шляхом замикання кола в певні моменти часу. Слід відмітити, що при цьому час релаксації вимірюючих приладів повинен бути надзвичайно малим, інакше будуть передаватись не , а перехідні функції приладів!

Пристрої, на приймальному кінці каналу зв‘язку, що відновлюють повинні реалізувати зв'язок між таз допомогою рядів Котельникова.

Загальна структура пристрою:

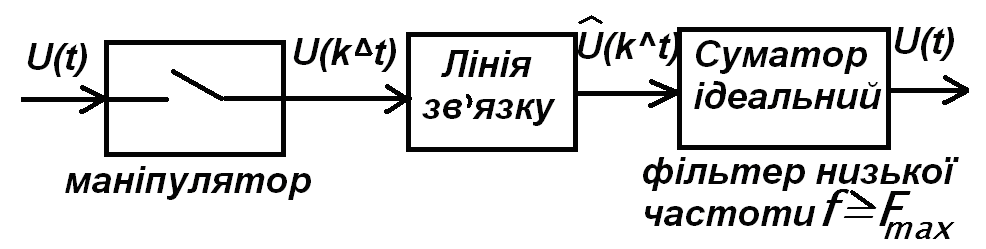
Обмеження використання теореми Котельникова для реальних сигналів передачі:

1. підлягають передачі лише сигнали з обмеженим спектром

2. при реалізації передачі необхідні маніпулятори, що мають дуже малі часи релаксації;

3. необхідно використовувати ідеальні фільтри низьких частот.

Оскільки реальні сигнали мають необмежений спектр, а функція відліків встановлена для строго обмежених спектрів, то фільтр НЧ необхідно брати з дещо ширшою, на 10 - 15% за необхідну, смугою пропускання. Наприклад, якщо частота сигналу обмежена Гц то, в системах з імпульсними способами передачі інформації, його слід передавати з частотою 6800 Гц. Фільтри НЧ і частота роботи вибирається 8000 Гц.

2.4.4.Теорема Котельникова в електрозв’язку, багатоканальний варіант (без).

Нехай потрібно передати дві часові залежності через канал зв’язку утворюючи (БЕЗ).

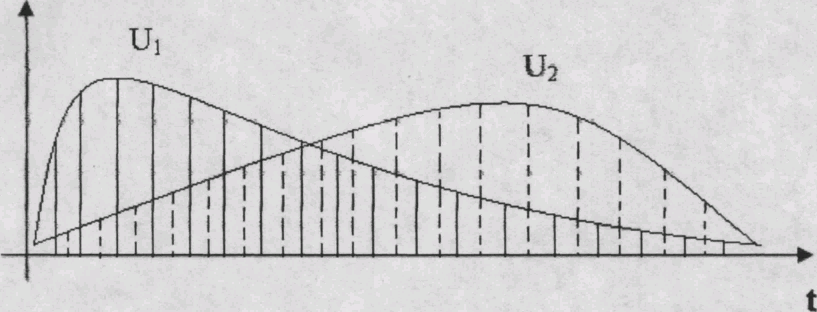
Оскільки інформація передається імпульсами з значною шпаруватістю, то парні імпульси несуть інформацію про , а непарні про , при цьому задовільняє теоремі Котельнікова як для одної так і для іншої функції. В даний час реалізовані системи БЕЗ з часовим розділенням що налічують 12, 15, 30, 120, 480, 960 розмовних сигналів по одній лінії.