Вопрос 28. Окружность

Изучение уравнении второго порядка, описываемы уравнениями второй степени. Начнем с окружности с центром O (x_o;y_o), радиусом R и точкой M(x₁;y₁).

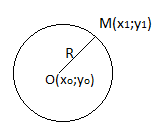
По определению, для любой точки М окружности вып-ся равенство |OM|=R.Используя формулу расстояния между двумя точками получим:

√(x-x_o)²+(y-y_o)²=R или то же самое (x-x_o)²+(y-y_o)²=R² (5)-нормальное ур-е окружности.

В частности если центр окружности в начале координат, то ее ур-е x²+y²=R² .

Рассмотрим общее ур-е второй степени с 2 переменными:

Ax²+Bxy+Cy²+Dx+Ey+F=0 (6)

A²+B²+C²≠0? A,B,C-одновременно не 0.

Выясним, при каких условиях ур-е (6)- есть ур-е окружности. Для этого (5) раскроим скобки и запишем

x²+y²-2x_ox-2y_ox+x_o²+y_o²-R²=0 (7)

Для того, чтобы (6) и (7) описывают одну и ту же линию, необходимо , чтобы коэф-т В=0, т.к. ур-е (7) не содержит x,y, а……………………………..

=> A=C≠0

Получим : Ax²+Ay²+By+Ey+F=0 (8)

Уравнение (8) называется общим уравнением окружности.

Разделив обе части уравнения на А и заполнив члены содерж. х,у получим:

(x+)² +(y+)²= (𝒟²+² -4AF)/4 A² (9)

Cсравнив (9) с уравнением окружности (5) можно сделать вывод , что (6) –есть уравнение окружности , тогда B=0, A=C и 𝒟²+² -4AF >0.

При выполнении этих условий центр окружности расположен в точке O (

а R= √(𝒟²+² -4AF)/2A.

Вопрос 29. Эллипс.

Эллипсом называется множество всех точек плоскости, сумма расстояний которых до 2х данных точек называемыми фокусами, есть величина постоянная, большая чем расстояние между фокусами.

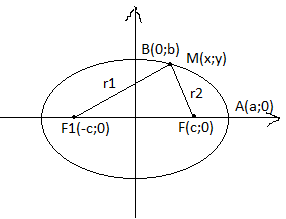
Обозначим F1 и F2-фокусы эллипса. Расстояние |F1F2|=C. Сумму расстояний от производной точки эллипса до фокусов обозначим через 2а .

По определению эллипса а>c, Для вывода уравнения эллипса введем параллельную систему координат к, чтобы фокусы эллипса лежали на оси абсцисс, а начало координат делило F1F2 пополам.

Пусть M(x;y)- произвольная точка плоскости. Обозначим расстояние r1=|F1M|, r2=|F2M|

Из определения эллипса следует, что точка M(x;y) будет лежать на эллипсе когда r1+r2=2a (1)

По формуле расстояние между 2мя точками мы можем переписать

=2a (3)

Урвнение (3)-есть ур-е эллипса. Но оно неудобно для использования.

Преобразуем :

Перенесем один радикал вправо и возведем обе части в квадрат.

Получим :

(x+c)² + y²=4a²-4a +(x-c)²+y²

Приводя подобные члены, получим:

a√((x-c)²+y²)=a²-cx (4)

Снова возведем обе части в квадрат

После упрощения получим:

(a²-c²)-x²+a²y²=a²(a²-c²) (5)

Обозначим ч/з b=√(a²-c²), тогда (5) ур-е примет вид: b²-x²+a²y²=a²b²

Разделив обе части на a²b², окончательно получим x²/a²+y²/b²=1 (6)

Любая точка координат которая удовлетворяет (6)-есть уравнение эллипса. Уравнение (6) называется каноническим уравнением эллипса.

Заметим, что (6) содержит только четные степени, поэтому эллипс симметричен относительно осей OX и OY и относительно начала координат. Т.о., чтобы знать формулу всего эллипса достаточно установить вид той части его, которая лежит в первом квадрате.

Для этой части y≥0 (6)=>

y= (7) Из (7) следует:

1.если x=0, то y=b, следовательно B(0;b) лежит на эллипсе

2. при возрастании числа x<a, b<y<0

3.если x=a => y=0 , следовательно точка A(a;0) лежит на эллипсе

4. когда x>a => a2-x2<0, следовательно x>a на эллипсе нет.

Итак, частью эллипса распол. В первой координатном угла является дуга BA. Проведя симметрию относительно начала координат и оси получим эллипс.

Если a=b, ур-е => x²+y²=a² (эллипс-окружность) . Оси симметрии наз-ся осями эллипса, а центр симметрии O –центром эллипса точки в которых эллипс пересек. оси-его вершина.

Величины a,b=большая и малая полуось эллипса. Эксцентриситетом эллипса называется отношение , где с-половина расстояний м/у фокусами, а-большая полуось эллипса. Т.к. с<а, то 0≤E≤1.

Принимая во внимание , что c²=a²-b²

E²= = = 1-()² => =

И легко получится геометрическое истолкование эксцентриситета эллипса.

Т.о. эксцентриситет эллипса характеризует мру вытянутости эллипса. Как известно, планеты, нек. кометы движутся по эллипсическим траекториям. Оказывается, что эксцентриситеты планетарных орбит весьма малы, а кометы велики, то есть близки к 1.

Т.о., планеты движутся почти по окружности, а кометы приближаются к солнцу. Солнце находится в одном из фокусов, но значительно отдалено от него.