1.5 Множення рядів

Вище ми згадували про додавання та множення на константу рядів, а як же перемножити між собою два ряди? Чи завжди добуток двох збіжних рядів буде збіжним рядом? В цьому розділі ми дамо відповіді на ці запитання.

Розглянемо поняття добутку двох рядів за Коші.

Означення (Коші). Під добутком рядів

, (1)

(2)

за Коші, розуміють такий ряд

, де . (3)

Виявляється, що якщо ряди (1) і (2) – збіжні, то цього мало для збіжності ряду (3) (добутку їх за Коші).

Приклад. Нехай ми маємо два ряди і , утворимо добуток цих рядів

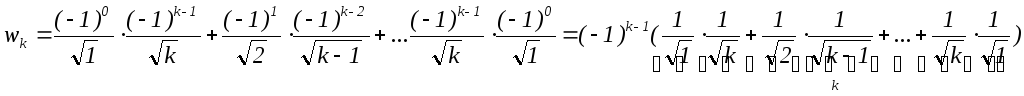
Взявши по модулю ми побачимо, що кожен доданок в дужках більший або рівний за , то врахувавши, що кількість доданків , матимемо, що і не прямує до нуля, а отже, ряд – розбіжний. Таким чином, ми встановили, що добуток двох збіжних рядів не зобов’язаний бути збіжним рядом.

Зауважимо, що обидва співмножники є умовно збіжними рядами. Можливо, негативний результат одержався саме з цієї причини? Відповідь на цю проблему дає наступне твердження.

Теорема. (Мертенс). Нехай ряд (1) абсолютно збіжний, а ряд (2) – збіжний. Тоді ряд (3) – збіжний до числа , де і – суми рядів відповідно (1) і (2).

▲

Нехай , , – часткові суми відповідно рядів (1), (2), (3). Розглянемо

(4)

Оскільки ряд (2) – збіжний до суми , то , а отже, , де при . Звідси і з (4) маємо, що . Для доведення цієї теореми достатньо показати, що

. (5)

З абсолютної збіжності ряду (1) маємо, що

, (6)

де – це число, що визначається з того, що нескінченно мала послідовність . – обмежена, і

. (7)

Оцінимо тепер ,

. Із збіжності ряду , випливає, що його сума дорівнює деякому числу , тоді

, . (8)

Оскільки , то для вказаного в (6) знайдеться

. (9)

Повертаючись до оцінки візьмемо , тоді на основі (9) та (8) матимемо, що , а це і означає, що ряд (3) – збіжний.

▼

Зауважимо, що в теремі Мертенса умова абсолютної збіжності одного з рядів не може бути знятою.