1.2 Знакододатні ряди. Умови збіжності таких рядів.

Означення. Ряд

(1)

називається знакододатнім, якщо всі члени цього ряду є невід’ємними дійсними числами. Як завжди, ряд (1) буде збіжним якщо . Вивчимо детальніше послідовність – часткових сум знакододатнього ряду. Очевидно для цього ряду послідовність є неспадною ().

З цієї властивості зразу випливає наступна

Теорема1. (Критерій збіжності знакододатнього ряду). Для того щоб знакододатній ряд був збіжний необхідно і достатньо, щоб послідовність його часткових сум була обмеженою.

Зауваження. Для знакододатнього ряду, точніше послідовності його часткових сум можливі два варіанти:

1. вона обмежена ( – знакододатній ряд збіжний)

2. вона необмежена ( – ця рівність замінює слова “знакододатній ряд розбіжний”).Якщо ж ряд не є знакододатнім, то останньою нерівністю не користуються для заміни слів “ряд збіжний”.

Звичайно, терема 1 в деякій мірі вирішує проблему збіжності знакододатнього ряду, але не завжди обмеженість послідовності розв’язується простіше чи набагато простіше ніж її збіжність. І тому добре було б мати якісь інші, конструктивніші, хоча б достатні умови збіжності знакододатніх рядів.Такі достатні умови є, і почнемо з такої

Теорема2. (Ознака порівняння рядів). Нехай

, (1)

(2)

– два знакододатні ряди. Якщо існує , таке що,

(3)

то із збіжності ряду (2) випливає збіжність ряду (1), а із збіжності ряду (1) випливає розбіжність ряду (2).

▲

Нехай і - послідовність часткових сум рядів (1) і (2), тоді з (3) матимемо, що

(4)

для . Нехай ряд (2) – збіжний, тоді за теоремою1, послідовність - обмежена. Тобто, . Звідси і з (4) маємо, що для , а це знову за теоремою1, означає, що ряд (1) – збіжний. Друга частина теореми теж одержується зі співвідношення (4).

▼

Зауважимо, що теорема2, зрозуміло, залишиться вірною, якщо (3) буде виконуватися не обов’язково для , а для починаючи з деякого.

Якщо скористатися цими зауваженнями, то теорему2 можна подати в дещо іншому, можливо більш практично-конструктивному вигляді.

Теорема3. (Гранична форма ознаки порівняння). Нехай знову маємо знакододатні ряди (1), (2) і . Тоді якщо і , то ряди (1) і (2) одночасно збіжні або розбіжні.

▲

Справді, з умови теореми маємо що, , причому можна вважати, що . Тоді, і , і доведення теореми 3 одержується із теореми 2.

▼

Теорема4. (Друга ознака порівняння). Нехай (1) і (2) – два знакододатні ряди (з відмінними від нуля членами), причому для справедлива нерівність

. (5)

Тоді, якщо ряд (2) збіжний, то ряд (1) теж збіжний, а якщо ряд (1) – розбіжний, то і ряд (2) – розбіжний.

▲

Візьмемо і напишемо нерівності (5) до номера і перемножимо їх. Одержимо, . Нехай , тоді , а з цієї нерівності, за теоремою2, зразу одержуємо те, що нам потрібно.

▼

Зауваження. Зрозуміло, що в цій теоремі, можна було б вимагати виконання нерівності (5) , починаючи з деякого .

Тепер з цієї ознаки, ми одержимо одну універсальну ознаку збіжності знакододатнього ряду.

Теорема5. (Ознака Куммера). Нехай дано ряд (1) і – деяка послідовність додатних чисел. Розглянемо послідовність . Якщо

, (6)

то ряд (1) – збіжний. Якщо послідовність така, що ряд – розбіжний і

, (*)

то ряд (1) – розбіжний.

▲

З (6) матимемо, що

. (7)

Звідси, для доведення збіжності ряду (1), достатньо довести збіжність знакододатнього ряду

(8)

Для цього розглянемо послідовність вона, як випливає з нерівності (7), буде монотонно спадною, крім того, вона обмежена знизу нулем, отже, за відомою теоремою, послідовність є збіжною, тому

. (9)

Записавши -ту часткову суму ряду (8), легко одержимо, що , а звідси, і з рівності (9), одержуємо збіжність ряду (8), а з нею і збіжність ряду (1) і , отже, перша частина ознаки Кумера доведена.

Далі із (*) маємо, що , а звідси, і з розбіжності ряду , за другою ознакою порівняння, одержуємо розбіжність ряду (1).

▼

Як видно, надаючи різних значень, ми одержуватимемо різні часткові випадки ознаки Куммера. Розглянемо деякі із них

1. Нехай . Зрозуміло, що ряд , . Тоді, якщо

, (10)

то ряд (1) – збіжний. З (10)маємо, . Тобто це означає, що існує таке число (замість можна взяти ), що

. (11)

Очевидно, що із (11) випливає (10). Отже, виконання нерівності (11) гарантує виконання нерівності (10), що дозволяє стверджувати збіжність ряду (1). Якщо ж для

, , (12)

то ряд (1) розбіжний. Отже, ми зараз одержали наступне важливе твердження.

Теорема6. (Ознака Даламбера). Нехай ряд (1) – знакододатній, тоді:

1. якщо існує числ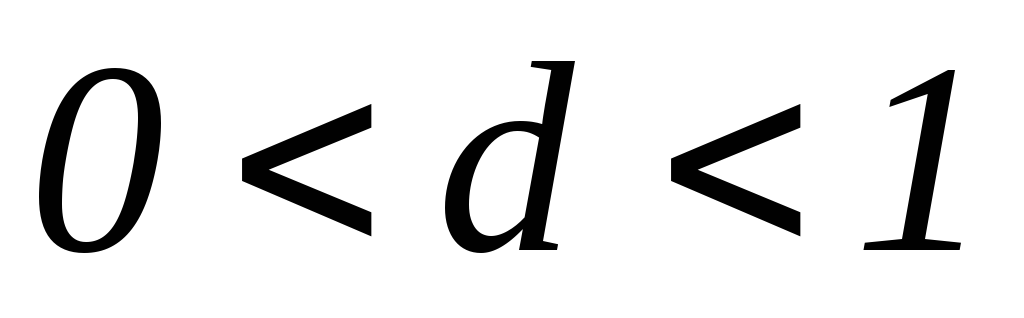о , () таке, що виконується нерівність , то ряд (1) – збіжний;

2. якщо виконується нерівність , то ряд (1) – розбіжний.

Наслідок1. Нехай ряд (1) – знакододатній і існує , тоді :

1. якщо , то ряд (1) – збіжний;

2. якщо , то ряд (1) – розбіжний;

3. якщо , то інформації про збіжність чи розбіжність ряду дана ознака не дає.

На кінець ознаку Даламбера можна сформулювати ще й в такій формі

Наслідок2. (Ознака Даламбера в термінах верхньої і нижньої границі). Нехай (1) – знакододатній ряд. Тоді, якщо:

1) , то ряд (1) – збіжний;

2) , то ряд (1) – розбіжний;

3) , то відповіді про збіжність чи розбіжність ряду дана ознака не дає.

Зауважимо, що доведення обох цих наслідків легко одержується із теореми6, і ми пропонуємо читачу розібратись з цим самостійно.

2. Розглянемо , як ми знаємо . Далі, якщо

, (*)

то , або позначивши через , будемо мати,

. (**)

Очевидно, що із (*) випливає (**), а із (**) випливатиме (*). Співвідношення (**) напишемо дещо по-іншому,

. (**’)

Зрозуміло, що із (**’) випливає (*), а значить із (*) за ознакою Кумера маємо наступне:

Якщо для ряду і таке, що , то ряд буде збіжним.

Нехай таке, що , тоді матимемо: . Отже, якщо , то ряд є розбіжним. Таким чином, ми одержали наступну ознаку.

Теорема7. (Ознака Раабе). Якщо існує і існує , то знакододатній ряд є збіжним. Якщо ж , , то цей ряд є розбіжним.

З’ясуємо який вигляд матиме ознака Раабе у граничній формі. Міркуючи аналогічно до попереднього, очевидно отримаємо наступний

Наслідок1. (Ознака Раабе). Якщо існує , тоді, якщо , то ряд – збіжний, якщо , то ряд – розбіжний, якщо , то проблему збіжності ряду ця ознака не вирішує.

▲

Нехай спочатку і . З означення границі для даного існує . Звідси . А це за теоремою7 означає збіжність ряду . Якщо , то і за означенням границі маємо, , . А це знову за теоремою7 означає, вже тепер розбіжність ряду .

▼

Наслідок2. (Ознака Раабе). Нехай (1) – знакододатній ряд, тоді, якщо:

1) , то ряд (1) – розбіжний;

2) , то ряд (1) – збіжний;

3) , то відповіді про збіжність чи розбіжність ряду дана ознака не дає.

Порівняємо силу ознак Раабе і Даламбера. Будемо використовувати їх перші граничні форми. Якщо для ряду (1) ознака Даламбера дає позитивну відповідь на проблему збіжності, то . Тоді , і ми одержали збіжність ряду (1) і за ознакою Раабе. Отже, якщо збіжність ряду встановлена за ознакою Даламбера, то і ознака Раабе теж підтверджує його збіжність. Аналогічно і для розбіжності ряду. Розглянемо ряд , який є узагальненим гармонійним рядом. Застосуємо до нього ознаку Раабе, оскільки ознака Даламбера тут не підходить (): , згідно цієї ознаки, маємо, якщо , то ряд збіжний, а якщо - розбіжний. Цей приклад показує, що ознака Раабе є сильнішою від ознаки Даламбера.

Перед тим, як розглядати ще один випадок ознаки Куммера подивимось на ознаку, яка хоча і немає великого спектру застосування, проте в окремих випадках ефективна і пов’язує ряди з невласними інтегралами.

Інтегральна ознака Коші. Нехай функція задана на проміжку , така, що:

1) , ;

2) – монотонно спадна на .

Тоді невласний інтеграл і ряд – одночасно збіжні, або розбіжні.

▲

Візьмемо , з умови 2) випливає, що . Спочатку проінтегруємо цю нерівність, а потім просумуємо від 1 до k . Матимемо:

, ;

, або

, , (1)

де – -та часткова сума ряду .

Припустимо, що невласний інтеграл є збіжним. Це означає, що послідовність {} теж збіжна, а отже, обмежена; тобто . Звідси із (1) випливає, що {} є обмеженою, а оскільки, вона ще і монотонно неспадна, то збіжна. Це , в свою чергу, означає, що ряд – збіжний.

Нехай, тепер збіжним є ряд , тоді послідовність {} теж збіжна, а отже, обмежена. Тому, . Звідси і з нерівності (1) маємо, що

, . (2)

Оскільки, послідовність інтегралів {} монотонно неспадна (бо , ), то з (2) випливає, що

. (3)

Візьмемо далі , тоді, очевидно що . З цієї умови і того, що на випливає . А згідно умови (3) отримуємо, що невласний інтеграл – збіжний (тут ми скористалися відомою теоремою про „два міліціонери”). Випадок розбіжності розглядається аналогічно.

▼

Застосуємо на прикладі щойно доведену ознаку. Візьмемо ряд

,

1) , ;

2) монотонно спадна, бо на цьому проміжку монотонно зростаюча.

Візьмемо , а отже, ряд - розбіжний.

Повернемося знову до ознаки Куммера і покладемо, що в ній , і позначимо через . Тоді для матимемо, що

Оскільки, другий доданок правої частини рівності прямує до одиниці при , то якщо ,, то ряд є збіжним. Якщо ж , то ряд – розбіжний.

Таким чином, ми з ознаки Куммера одержали ще одну ознаку.

Теорема9. (Ознака Бертрана). Якщо для знакододатнього ряду то цей ряд збіжний, якщо ж , то ряд розбіжний.

Наслідок1.(Ознака Бертрана у граничній формі). Якщо , то при – ряд збіжний, при – розбіжний, при – відповіді про збіжність чи розбіжність дана ознака не дає.

Ознака Бертрана не є слабкішою за ознаку Раабе, а існують приклади, які показують, що вона є сильнішою. Пропонуємо читачу знайти такі приклади.

Зрозуміло, що як і в попередніх випадках можна одержати і

Наслідок.(Ознака Бертрана в термінах верхньої і нижньої границь). Якщо , то цей ряд розбіжний, якщо , то ряд збіжний, а якщо , то дана ознака відповіді на питання збіжності не дає.

Розглянемо, на кінець ще одну ознаку, яка не одержується, як попередні, із ознаки Куммера.

Теорема10. (Ознака Коші (радикальна)). Нехай – знакододатній ряд. Якщо

, (*)

то цей ряд збіжним, якщо ж , то наш ряд – розбіжний.

▲

Позначимо , де - з умови теореми, тоді з (*) матимемо, що , , але ж ряд є збіжною геометричною прогресією, а тому із останньої нерівності випливає збіжність ряду за ознакою порівняння. Що стосується другої частини ознаки Коші, то з її умови випливає, що існує безліч членів ряду які більші або рівні одиниці, тому загальний член ряду не прямує до нуля і ряд розбіжний.

▼

Наслідок1. (Ознака Коші (радикальна) в граничній формі). Нехай – знакододатній ряд, причому, . Тоді, якщо:

– ряд збіжний,

– ряд розбіжний,

– відповіді ознака не дає.

Дуже часто трапляються випадки, коли у сформульованій вище ознаці границі не існує, тоді використовують іншу форму цього твердження.

Наслідок2. (Ознака Коші (радикальна) в термінах верхньої і нижньої границь). Нехай – знакододатній ряд, причому, . Тоді, якщо,

– ряд збіжний,

– ряд розбіжний,

– відповіді дана ознака не дає.