Ряди Числові ряди.

1.1 Поняття ряду. Збіжність, розбіжність ряду. Елементарні властивості числових рядів.

Нехай – деяка числова послідовність. Тоді нескінченну суму виду ми назвемо числовим рядом, і скорочено запишемо у вигляді

, (1)

числа назвемо відповідно першим, другим, третім, а – n- тим або загальним членом ряду.

Для того щоб з’ясувати, що розуміти під такою сумою і чи завжди вона існуватиме, поставимо у відповідність нашому ряду таку послідовність:

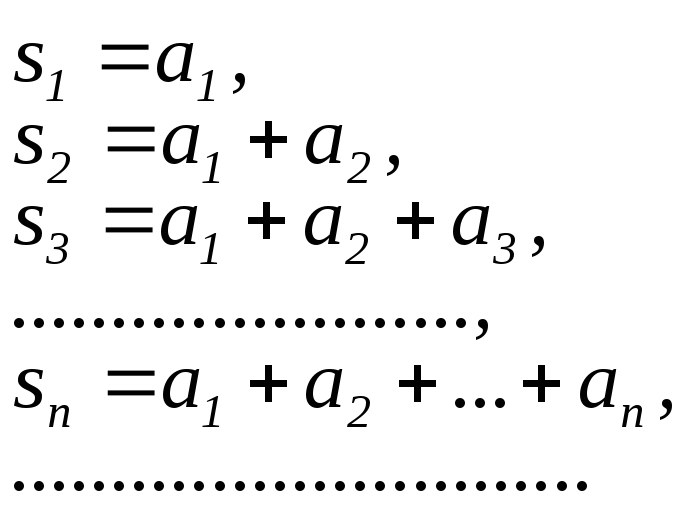
яку називатимемо послідовністю часткових сум ряду.

Означення. Якщо існує , то ряд (1) називатимемо збіжним, а число – його сумою.Якщо ж ця послідовність розбіжна, то і ряд також називатимемо розбіжним, тобто у цьому випадку він не матиме суми. Правда, якщо , то інколи кажуть, що ряд розбігається до нескінченності і його сума є нескінченно велика.

Зауважимо, що якщо ми маємо деяку послідовність , то зовсім неважко побудувати ряд для якого дана послідовність буде послідовністю його часткових сум. Справді, для цього достатньо покласти для .

Незважаючи на те що між рядами і послідовностями існує такий тісний зв’язок, теорія рядів є важливим розділом сучасної математики. Результати в ній не вичерпуються тими, які одержуються в теорії послідовностей. Тобто теорія числових рядів має самостійний інтерес і не зводиться лише до теорії числових послідовностей. Далі ми вкажемо на застосування цієї теорії, а зараз звернемо увагу на те, що в рамках шкільної математики ми, по-суті, використовували ряди, працюючи з нескінченними десятковими дробами. Хоча і теорія рядів є самостійним розділом математичного аналізу, і має серйозний інтерес, але поданий вище зв’язок між рядами і послідовностями дозволяє результати одного із цих розділів переносити на інший.

Проілюструємо це на такому прикладі. Ми знаємо, що для числових послідовностей має місце так званий критерій.

Критерій Коші. Для того щоб послідовність була збіжною необхідно і достатньо, щоб для ,або .

Оскільки, збіжність числового ряду еквівалентна збіжності послідовності його часткових сум, то звідси і з критерію Коші для послідовностей, враховуючи що таке і , отримаємо

Критерій Коші збіжності числового ряду. Для того щоб ряд був збіжним, необхідно і достатньо, щоб для .

Безпосередньо із самого означення збіжності ряду випливає один елементарний, але цікавий результат. Нехай ряд (1) збіжний, тоді за означенням існує (очевидно, що і ), але , тоді звідси і з останніх двох рівностей маємо . Таким чином, ми встановили наступне твердження

Необхідна умова збіжності ряду. Якщо ряд збіжний, то його загальний член прямує до нуля.

З цього результату зразу одержується

Достатня умова розбіжності ряду. Якщо загальний член ряду не прямує до нуля, то ряд розбіжний.

В зв’язку з цими результатами виникає таке запитання: а чи не буде необхідна умова збіжності ряду одночасно і достатньою умовою, тобто якщо , то чи не випливатиме, що ряд збіжний? Для відповіді на це питання розглянемо такий ряд,

(2)

який називається гармонійним рядом. Зрозуміло, що загальний член цього ряду прямує до нуля. З’ясуємо чи є цей ряд збіжним. Для цього візьмемо , для такого завжди знайдеться . Візьмемо тепер

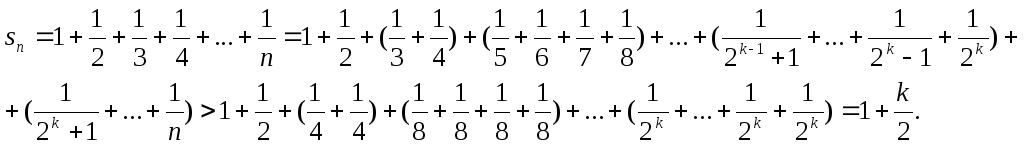
Отже, . З цієї нерівності маємо, що при , (а отже, і ) отримаємо, що і і тому ряд (2) розбіжний (до ). Таким чином, ми одержали, що гармонійний ряд розбіжний. Тим самим ми показали, що необхідна умова збіжності ряду не є достатньою, тобто, якщо , то звідси ще не випливає, що ряд буде збіжним.

Вище ми привели класичний приклад гармонійного розбіжного ряду. Наступним класичним прикладом, правда вже збіжного ряду, є геометрична прогресія

(3)

Очевидно, що при цей ряд буде збіжним, дослідимо його на збіжність при інших . При ряд (3) буде розбіжним, бо при такому загальний член не прямує до нуля. З'ясуємо, що буде коли . З курсу елементарної математики відомо, що.Тоді, . Це означає, що ряд (3) при є збіжним і його сума . Таким чином, зіставляючи це з одержаним вище, робимо висновок, що прямування загального члена ряду до нуля не дає ніякої інформації про збіжність чи розбіжність ряду.

З’ясуємо деякі простіші проблеми, пов’язані з арифметичними операціями над рядами.

Якщо і два збіжні ряди відповідно до сум А і В, то збіжними будуть і такі ряди відповідно до сум () і якщо , то збіжним буде ряд і його сума дорівнює . (Передостанні ряди називаються сумою чи різницею двох рядів, а останній ряд називається добутком ряду на число). Доведення цих фактів випливає з означення збіжності ряду.

Добре відомо, що коли ми маємо справу із сумою скінченої кількості доданків, то в цій сумі ми довільним чином можемо переставляти доданки чи групувати, це на суму не вплине. Чи можна це робити з рядами (нескінченими сумами)? Більш детально це питання буде розглядатися далі. А зараз обмежимось одним прикладом такого ряду . Очевидно, цей ряд розбіжний, бо . Розглянемо далі такий ряд , утворений ряд є збіжним і його сума дорівнює нулю. Отже, цей приклад показує, що ті властивості, що мали місце для скінчених сум на нескінченні суми, взагалі кажучи, не поширюються.