
Практическое занятие 1
|
Векторная алгебра |
|
|||||
|
1. Векторы, базисы, координаты |
|
|||||
|
№ |
Задание |
Ответ |
|
|||
|
1 |
В РЕШЕНИЕ:
Пусть
Воспользуемся
свойством биссектрисы треугольника
|
|
|
|||
|
2 |
Д РЕШЕНИЕ:
Пусть
Отложим от
вершины
Но это координаты
вектора
|
|
|
|||
|
3 |
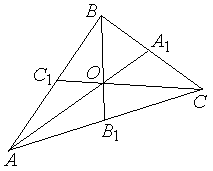
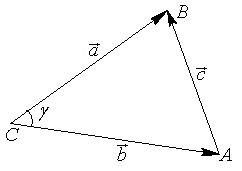
В треугольнике
РЕШЕНИЕ:
О
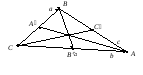
Из рисунка по
свойству медиан получаем, что
|
|
|
|||
|
4 |
Т РЕШЕНИЕ:
Если
|
|
|
|||
|
5 |
Н Доказательство:
Пусть
Отсюда
|
|
|
|||
|
6 |
З РЕШЕНИЕ:
Воспользуемся
правилом треугольника:
Подставим
|
|
|
|||
|
7 |
В РЕШЕНИЕ:
Пусть
Найдем:
После последовательных подстановок
то есть
|
|
|
|||
|
2. Декартов прямоугольный базис. Направляющие косинусы и координаты |
|
|||||
|
8 |
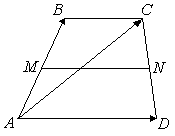
В трапеции
РЕШЕНИЕ:
|
3 |
|
|||
|
9 |
Даны точки
РЕШЕНИЕ:
Сумма координат равна (- 6). |
- 6 |
|
|||
|
10 |
Дан модуль
вектора
РЕШЕНИЕ:
|
|
|
|||
|
11 |
Даны векторы
РЕШЕНИЕ:
|
|
|
|||
|
12 |
Может ли вектор
составлять с координатными осями
следующие углы:
РЕШЕНИЕ:
Для направляющих
косинусов выполняется равенство
|
да |
|
|||
|
13 |
Д РЕШЕНИЕ:
Координаты точки
|
7 |
|
|||
|
14 |
Коллинеарны ли
векторы
РЕШЕНИЕ 1:
РЕШЕНИЕ 2
Векторы :
|
нет |
|
|||
|
3. Скалярное произведение векторов |
||||||
|
15 |
Найдите а)
РЕШЕНИЕ:
а)
|
а)
б)
|
|
|||
|
16 |
Найдите
РЕШЕНИЕ:
|
|
|
|||
|
17 |
Найдите косинус
угла между векторами
РЕШЕНИЕ:
|
- 1 |
|
|||
|
18 |
Вычислите синус
угла, образованного векторами
РЕШЕНИЕ: Найдем косинус нужного угла:
Так как угол
между векторами
|
|
|
|||
|
19 |
Покажите, что сумма квадратов медиан треугольника относится к сумме квадратов его сторон, как 3:4. РЕШЕНИЕ:
П
Осталось найти требуемое отношение:
|
|
|
|||
|
20 |
П РЕШЕНИЕ:
|
|
|
|||
|
21 |
Докажите, что
вектор
РЕШЕНИЕ:
|
|
|
|||
|
22 |
Д Доказательство:
а) Рассмотрим
треугольник
Пусть третья
сторона
б) При
|
|
|
|||
|
23 |
Д РЕШЕНИЕ:
Пусть
|
|
|
|||
|
4. Векторное произведение векторов |
|
|||||
|
24 |
Найдите а)
Решение:
а)
б)
так как
|
а)
б)
|
|
|||
|
25 |
Найдите
Решение:
|
|
|
|||
|
26 |
Найдите вектор
Решение:
|
|
|
|||
|
27 |
Упростите
выражение:
Решение:
Для
Тогда
|
|
|
|||
|
28 |
Векторы
Доказательство: Найдем
значит, эти векторы коллинеарны. |
|
|
|||
|
29 |
Вычислите площадь
параллелограмма, построенного на
векторах
Решение:
=< так как
|
|
|
|||
|
30 |
В Решение:
Площадь
Найдем
|
5 |
|
|||
|
31 |
Н Решение:
Построим
треугольник
Тогда искомое
расстояние равно
|
5 |
|
|||
|
32 |
Д Доказательство:
1)
2)
Отсюда следует,
что
|
|
|
|||
|
5. Смешанное произведение векторов |
|
|||||
|
33 |
Докажите, что
при любых
Доказательство:
Вычислим
|
|
|
|||
|
34 |
Докажите тождество
Доказательство:
|
|
|
|||
|
35 |
Даны векторы
а) вычислите объем параллелепипеда, построенного на этих векторах; б) вычислите объем тетраэдра, построенного на этих векторах;
в) определите,
будут ли векторы
г) определите,
образует ли тройка
д) определите,
будет ли тройка
Решение:
а).
б).
в). Так как
г). Образуют базис в трехмерном пространстве.
д).
|
7,
нет, да, левая |
|
|||
|
36 |
В Решение:
|
|
|
|||
|
37 |
Найдите расстояние
от плоскости, проходящей через точки
Решение:
Построим тетраэдр
|
|
|
|||
|
38 |
Длины базисных
векторов
Решение:
Осталось найти
Найдем
Так как
|
|
|
|||
|
39 |
Дайте алгебраическое доказательство того, что смешанное произведение трех компланарных векторов равно нулю. Доказательство:
Даны три
компланарных вектора
Если
Если
|
|
|
|||
|
40 |
Докажите, что
четыре точки
Доказательство:
Точки
|
|
|
|||
|
41 |
Дан параллелограмм
Доказательство:
Если
|
|
|
|||

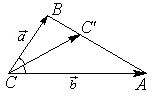 треугольнике
треугольнике
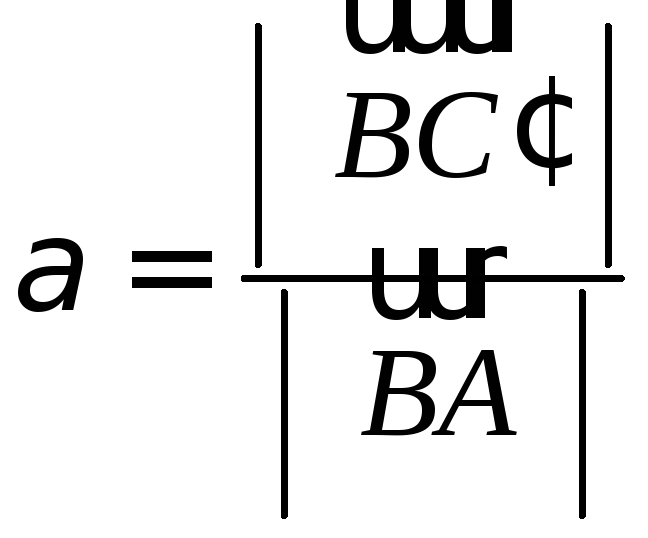 .
.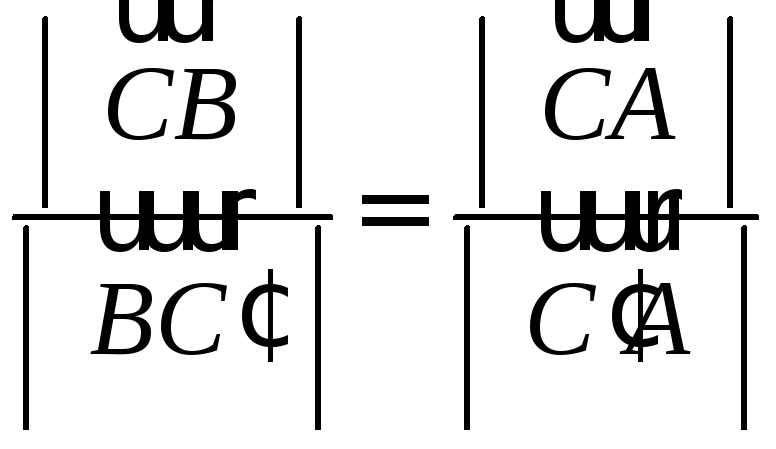 и тем, что
и тем, что
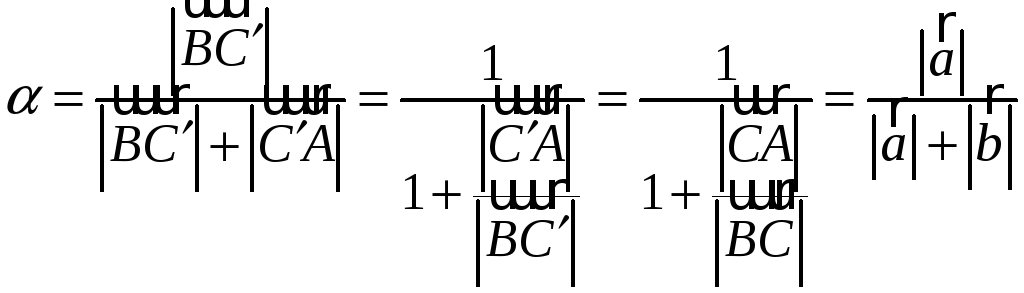 .
.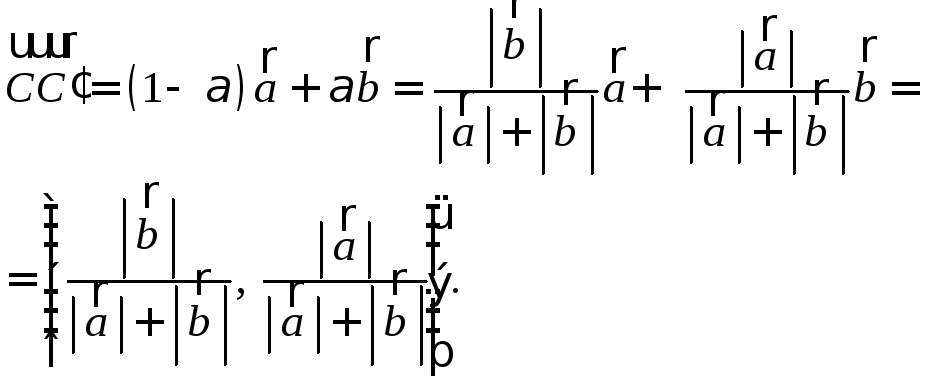
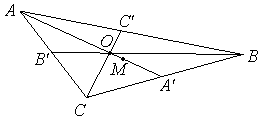 окажите,
что точка пересечения медиан
треугольника делит каждую медиану в
отношении
окажите,
что точка пересечения медиан
треугольника делит каждую медиану в
отношении
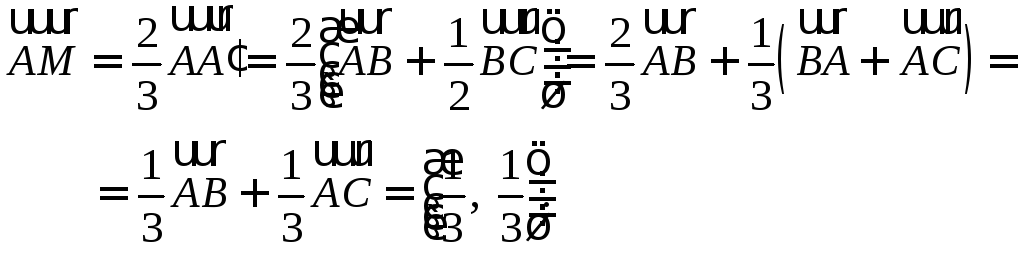
 бозначим
бозначим
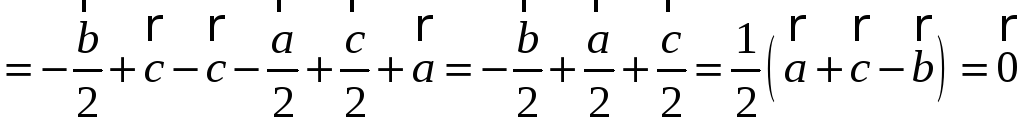 .
.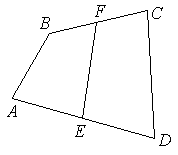 очки
очки
 а
стороне
а
стороне
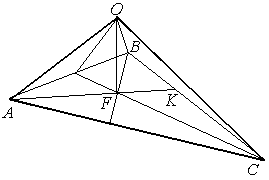 адан
тетраэдр
адан
тетраэдр
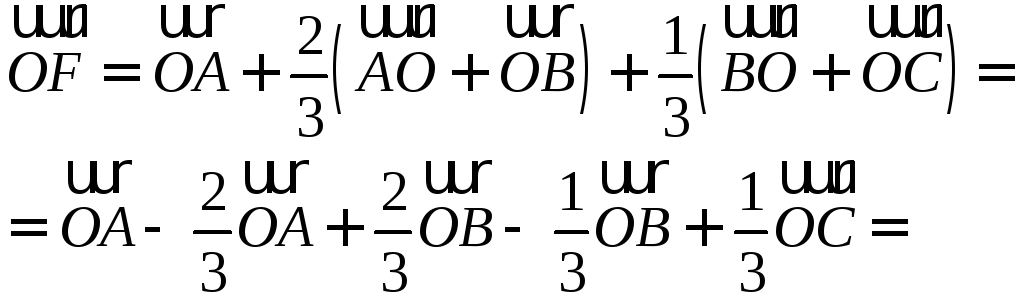
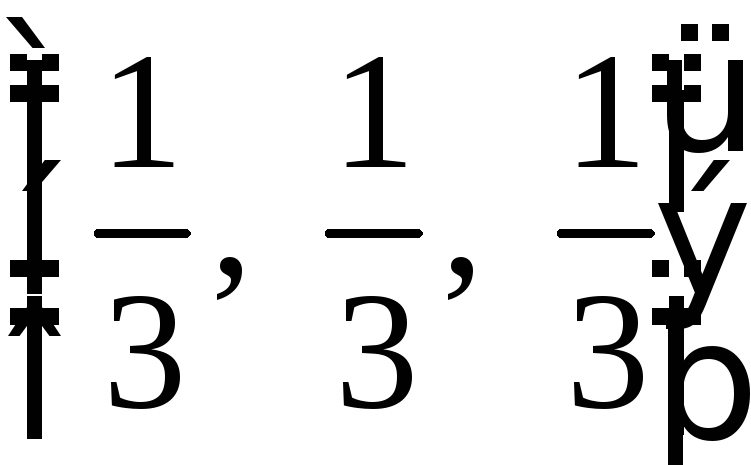 .
.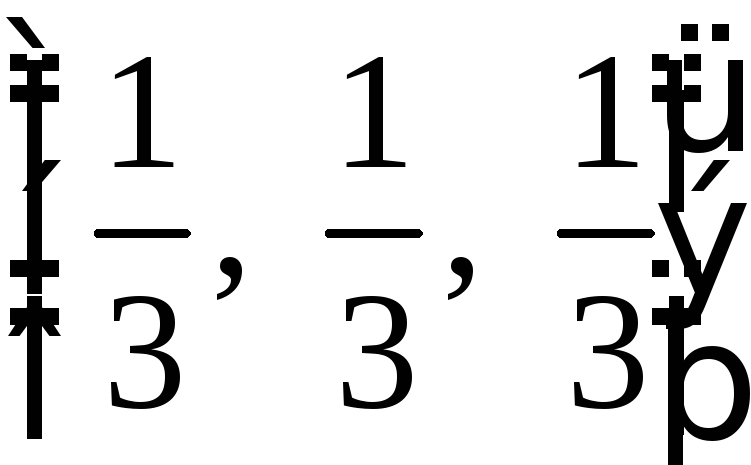
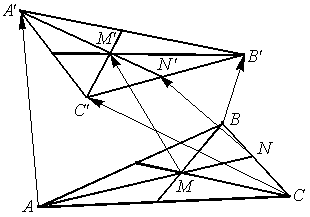 пространстве заданы треугольники
пространстве заданы треугольники
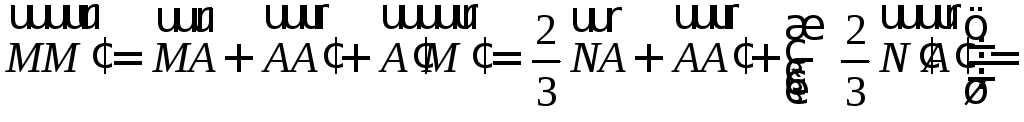
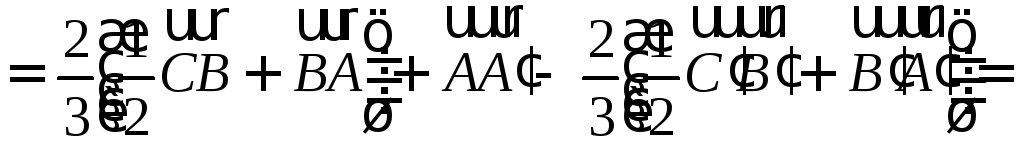
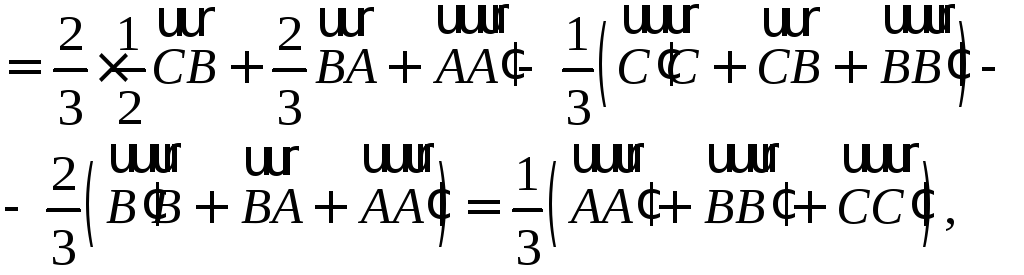
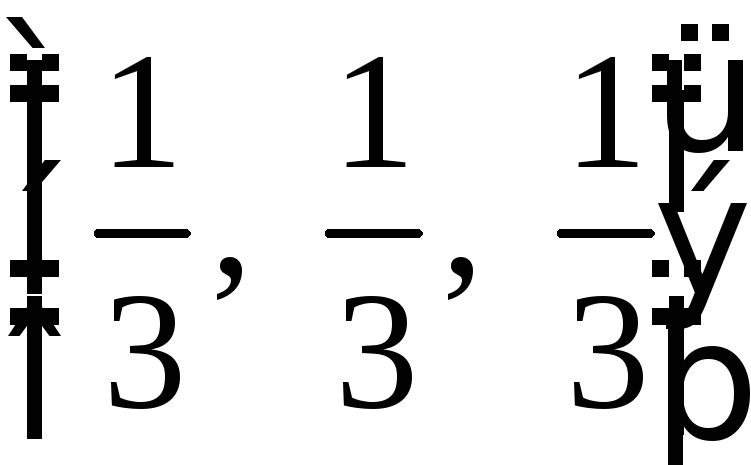 .
.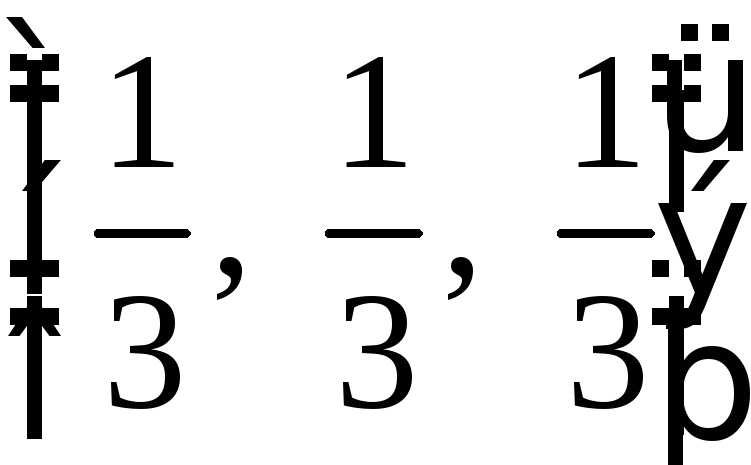
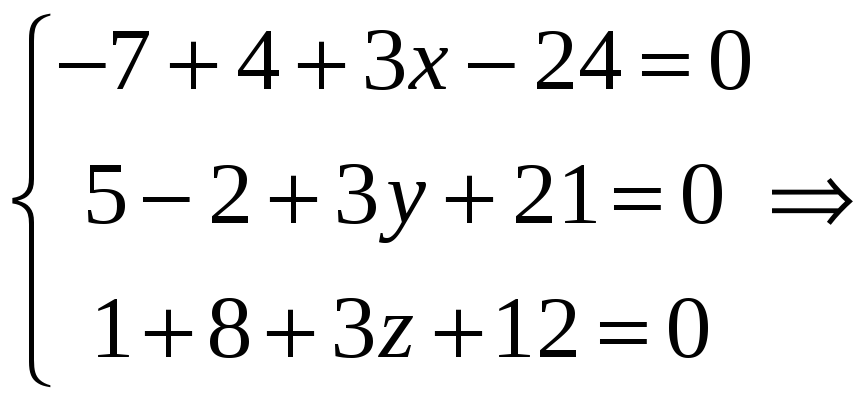
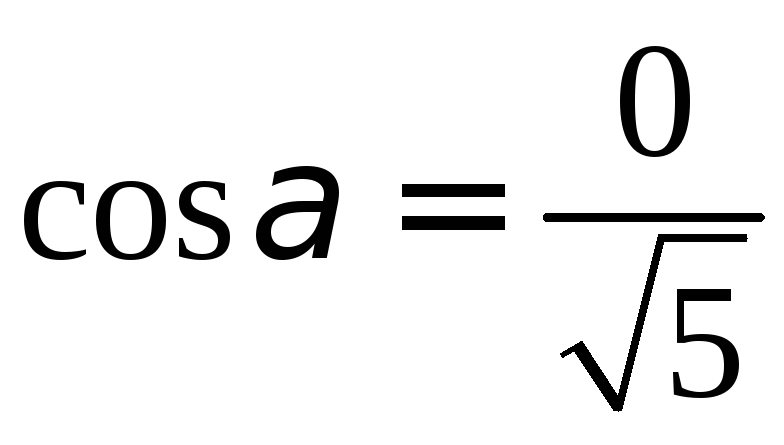 ;
;
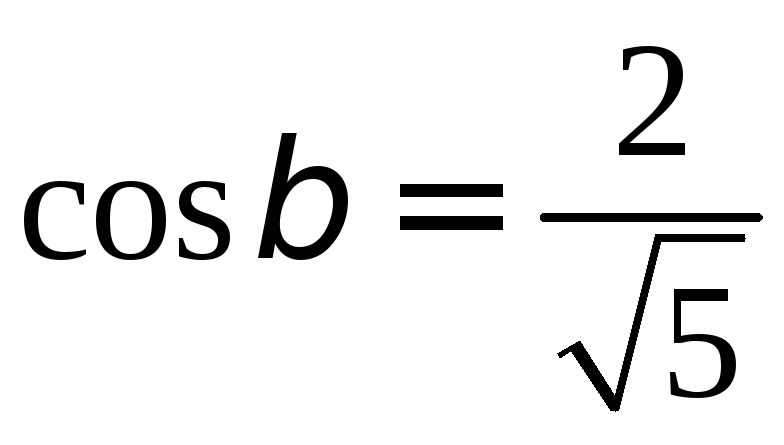 ;
;
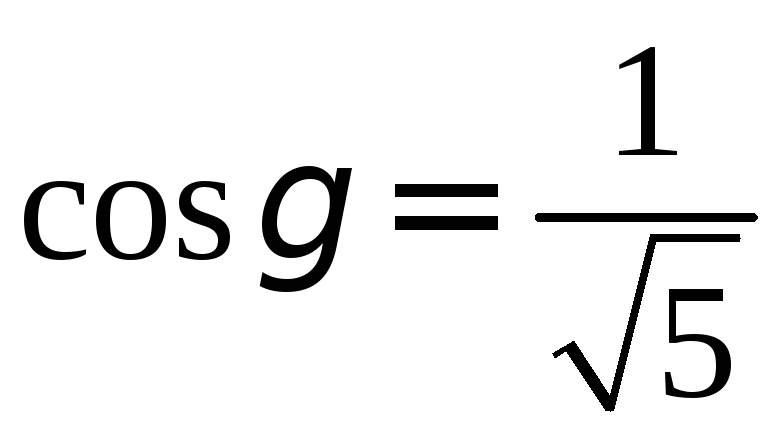 .
.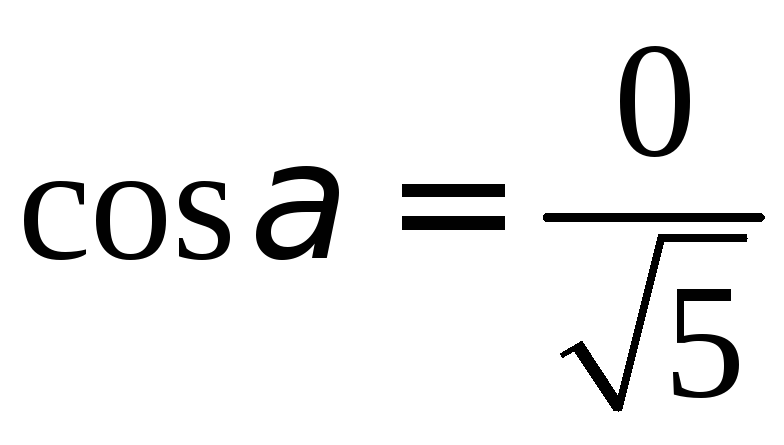 ,
,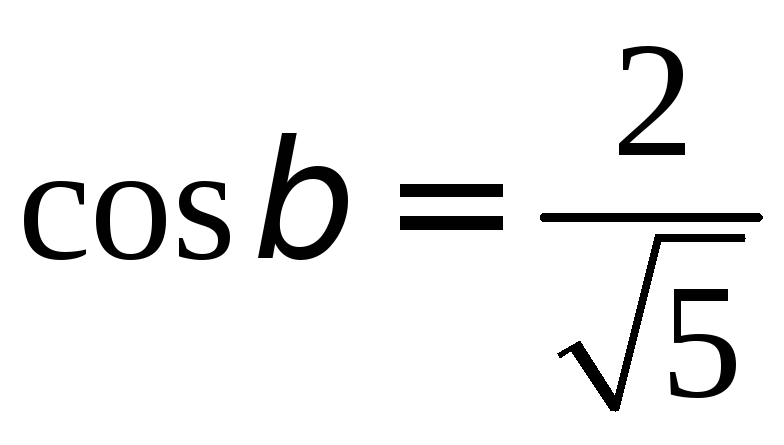 ,
,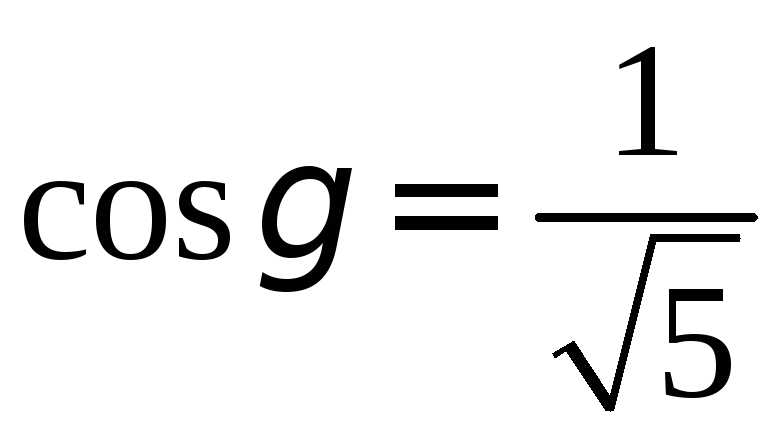
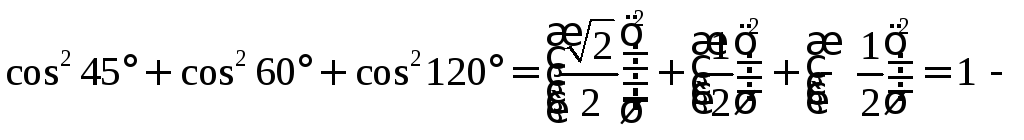 равенство
выполняется.
равенство
выполняется.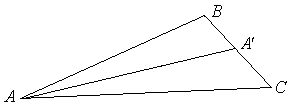 аны
точки
аны
точки
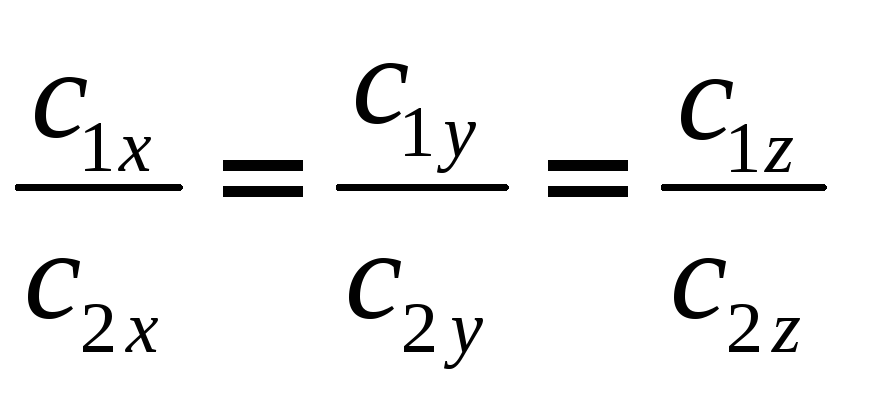 не выполняется, векторы неколлинеарны.
не выполняется, векторы неколлинеарны.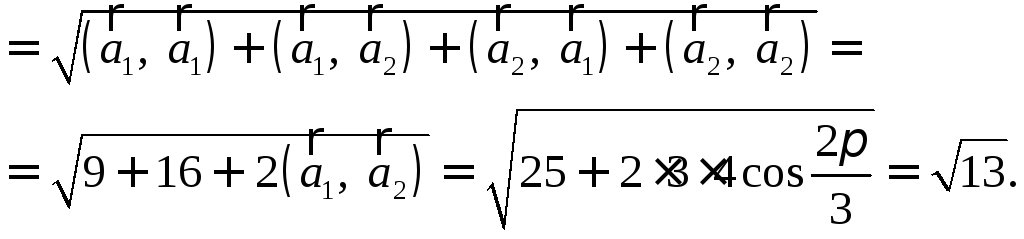
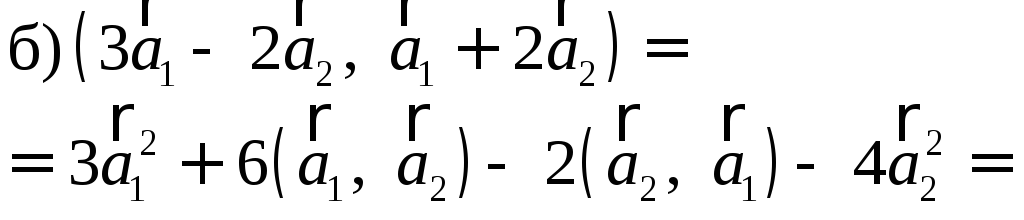
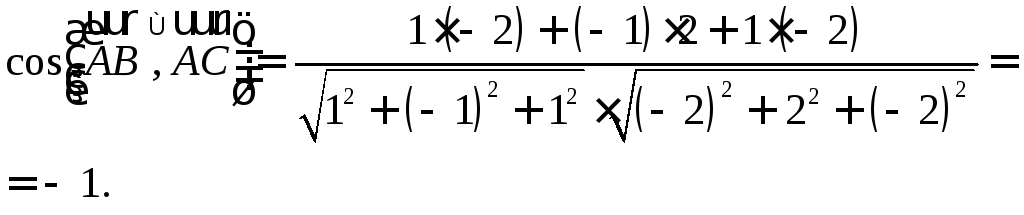
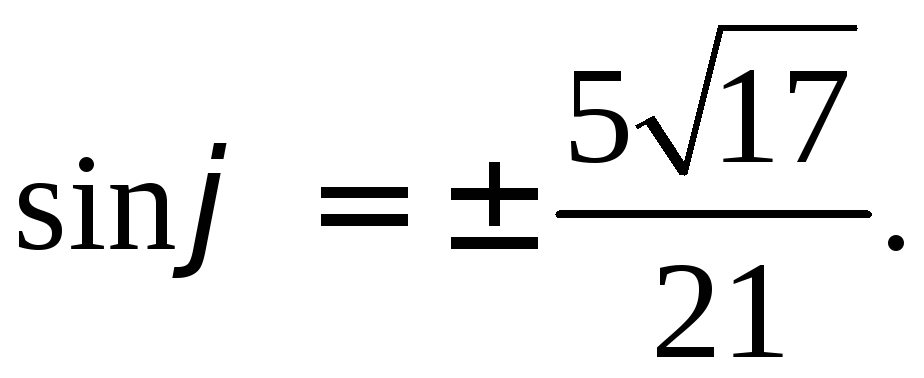
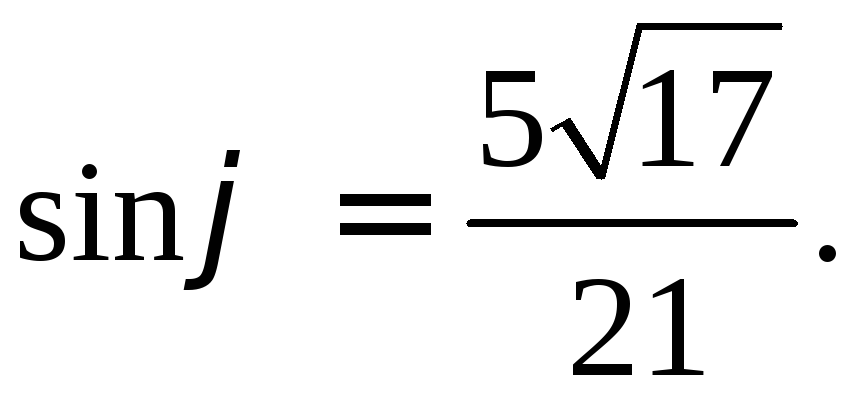
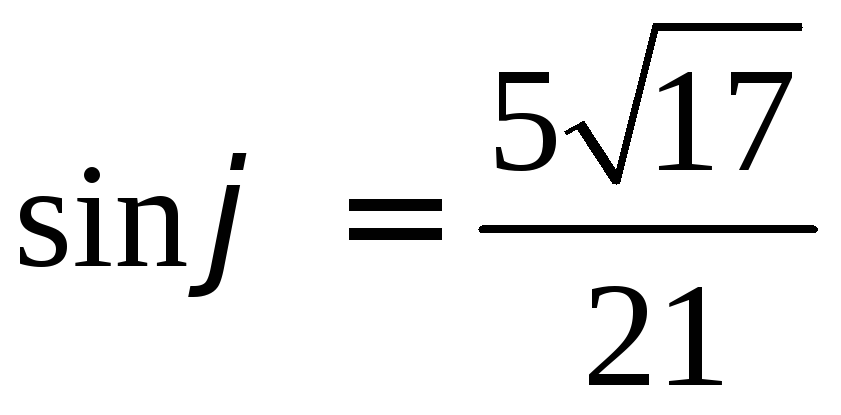
 усть
усть
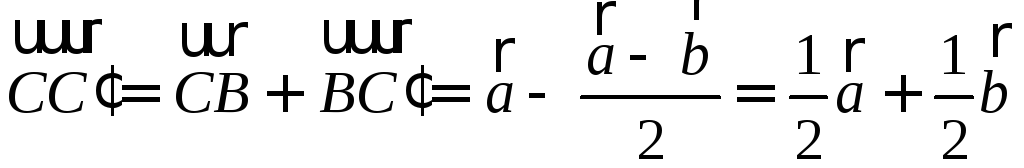 ,
,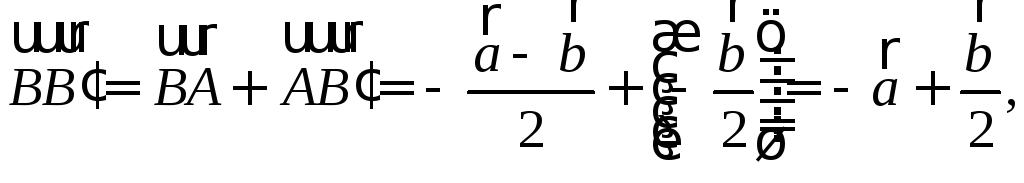
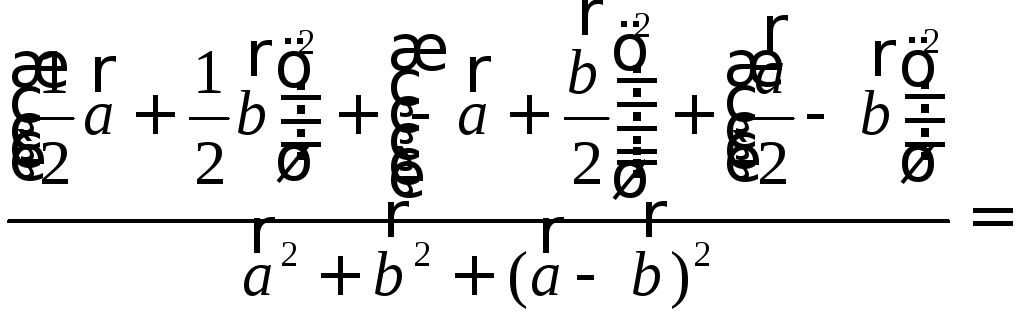
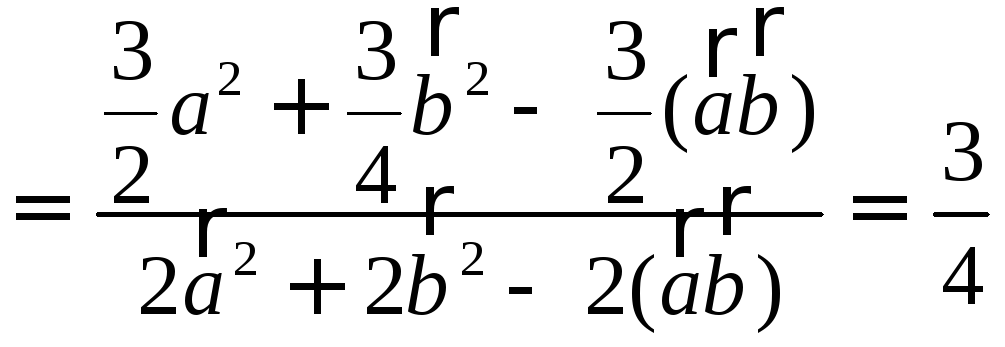
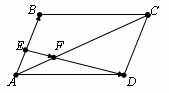
 окажите,
что четырехугольник
окажите,
что четырехугольник
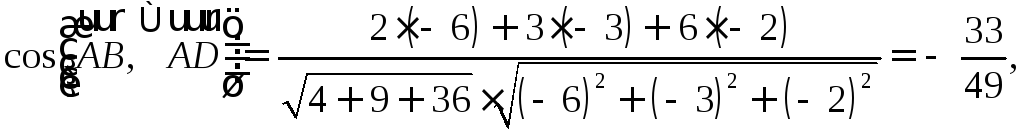 ,
,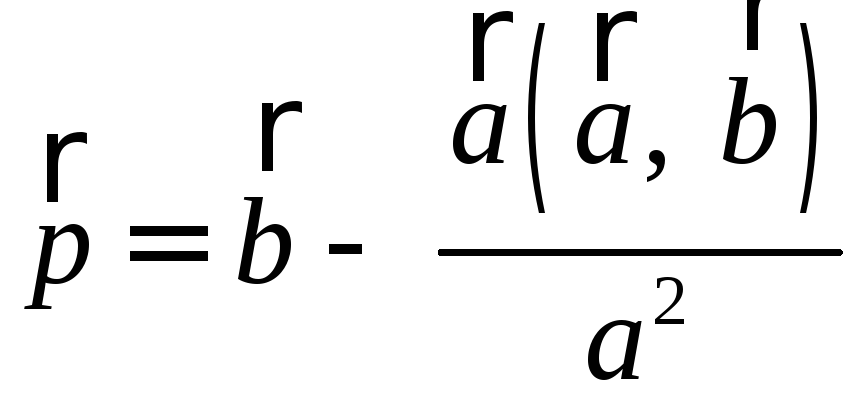 перпендикулярен вектору
перпендикулярен вектору
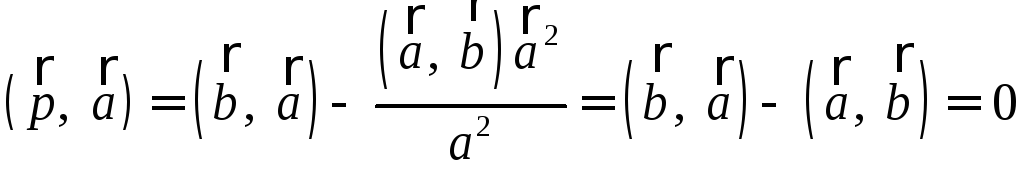 .
. окажите:
а) теорему косинусов; б) теорему
Пифагора.
окажите:
а) теорему косинусов; б) теорему
Пифагора.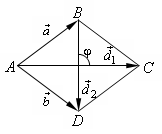 окажите,
что диагонали ромба взаимно
перпендикулярны.
окажите,
что диагонали ромба взаимно
перпендикулярны.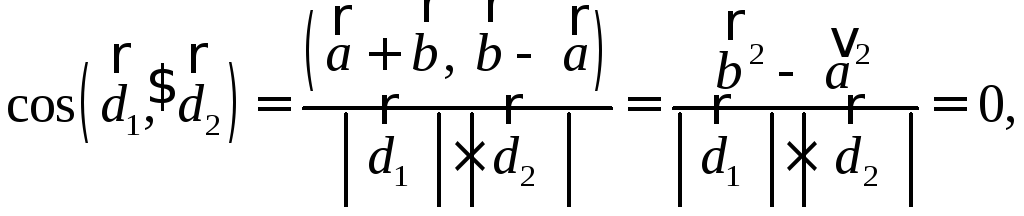 так как для ромба
так как для ромба
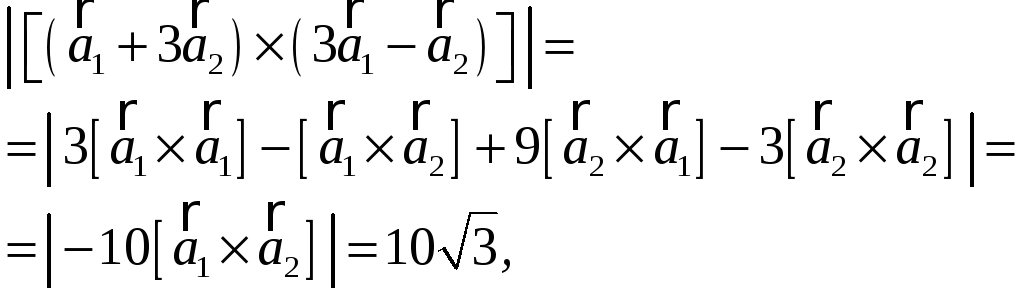

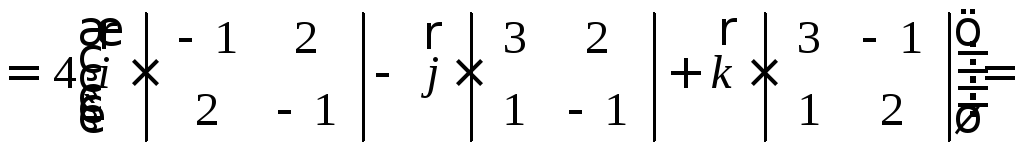
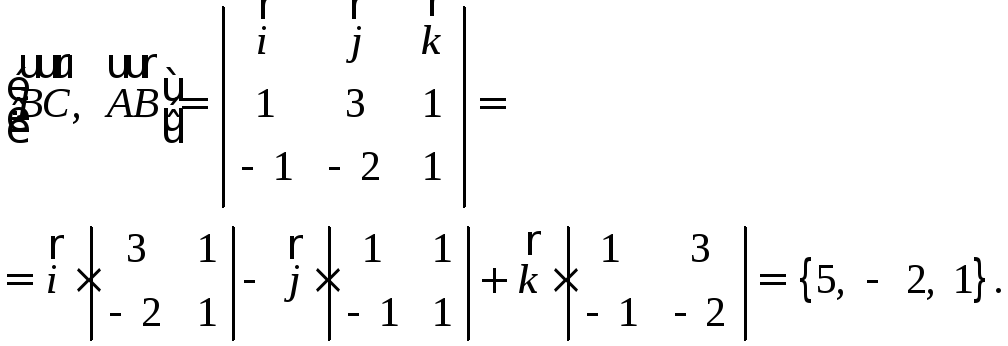
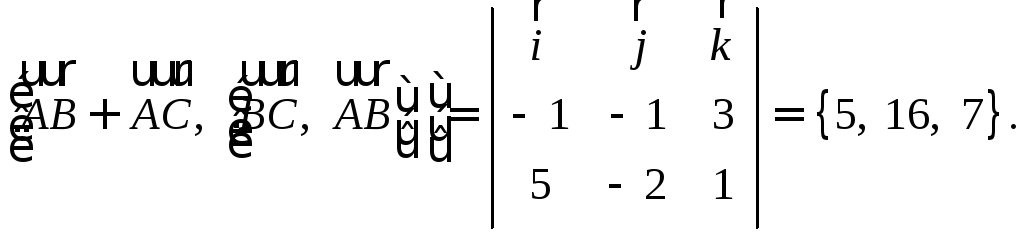
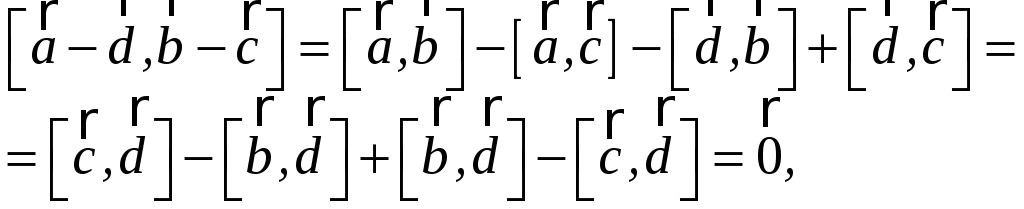
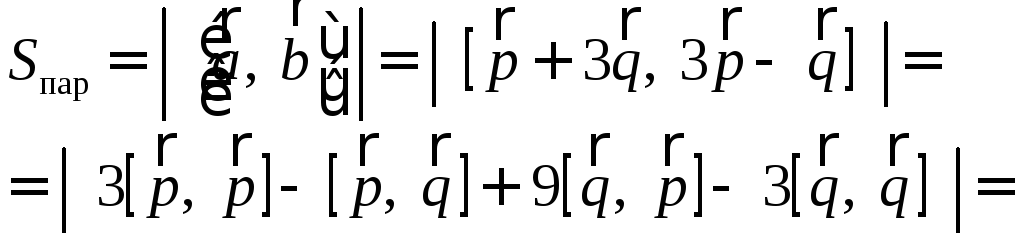
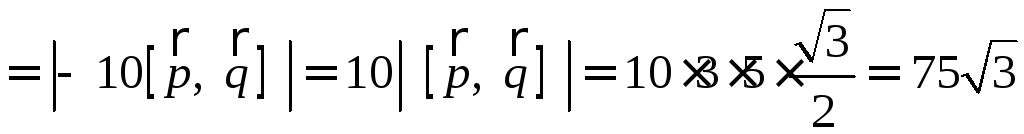 .
.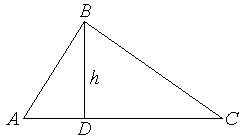 треугольнике с вершинами
треугольнике с вершинами
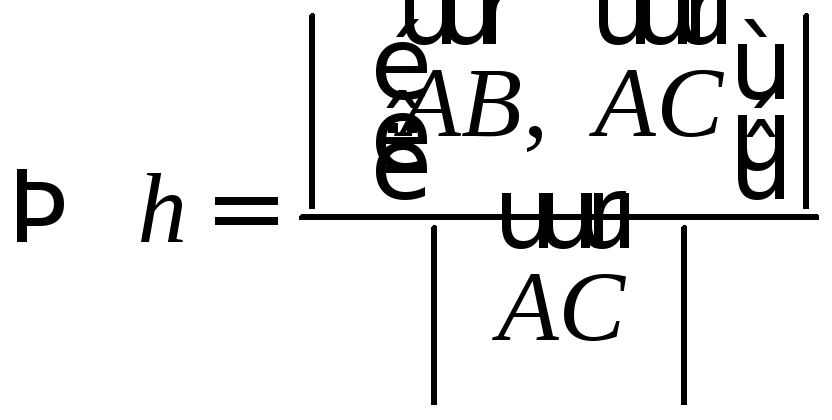 .
.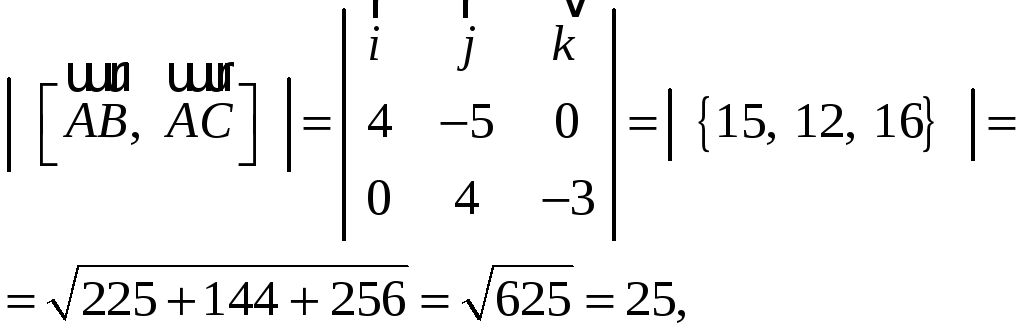 .
.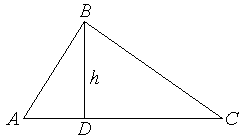 айдите
расстояние от точки
айдите
расстояние от точки
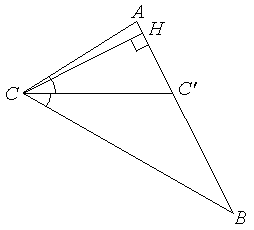 окажите,
что в треугольнике
окажите,
что в треугольнике
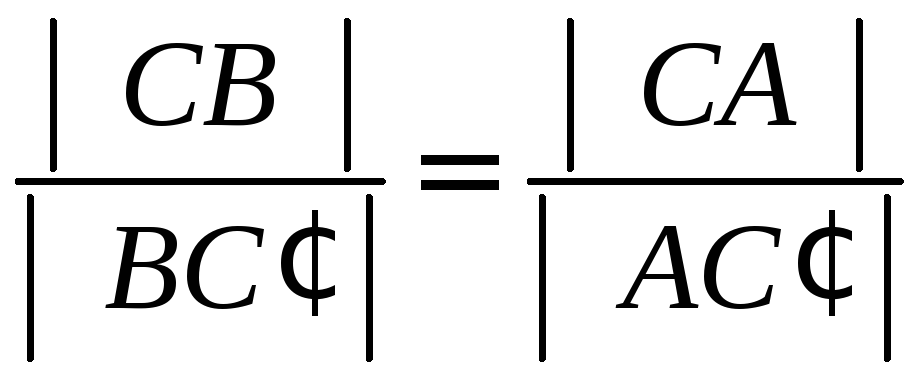 .
.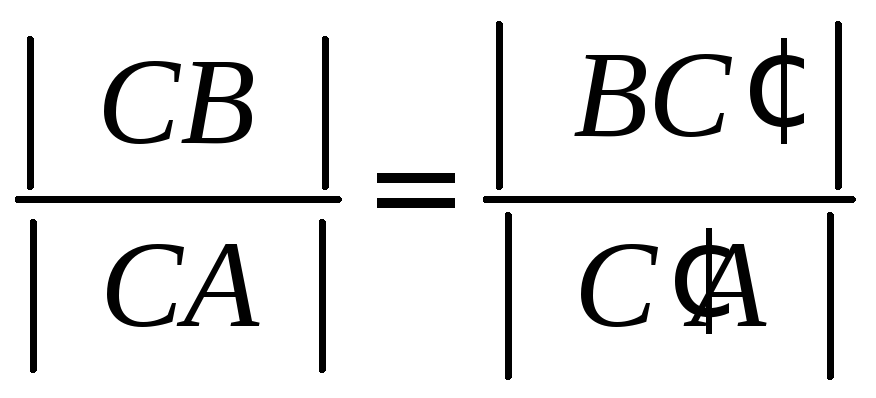 ,
что и требовалось доказать.
,
что и требовалось доказать.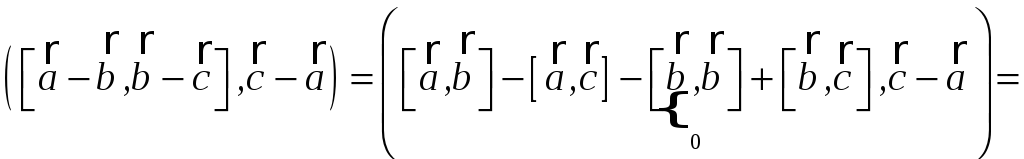
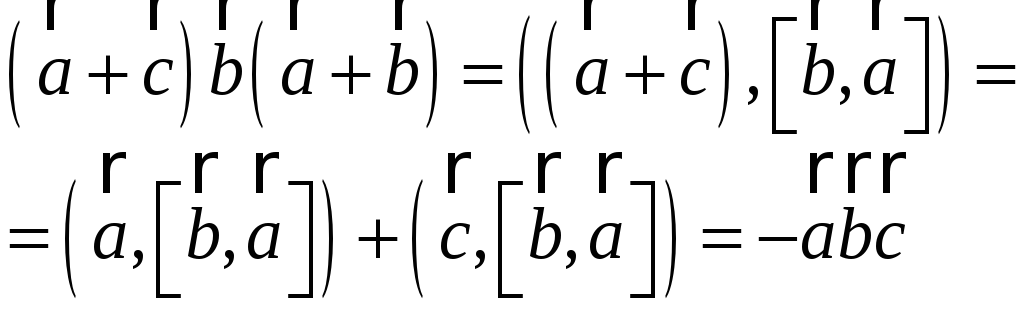 .
.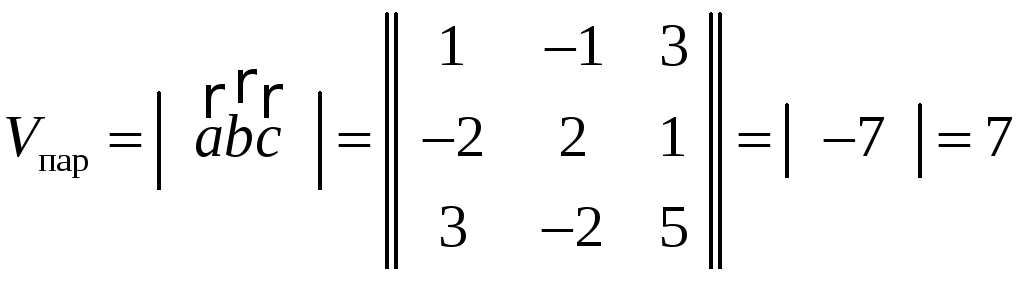 .
.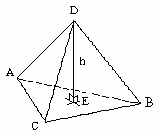 тетраэдре с вершинами в точках
тетраэдре с вершинами в точках
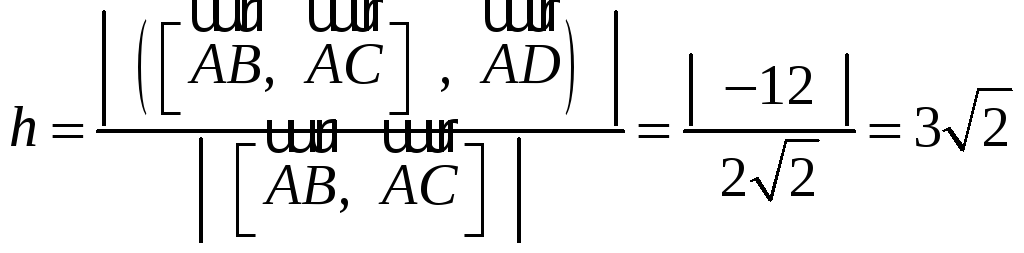
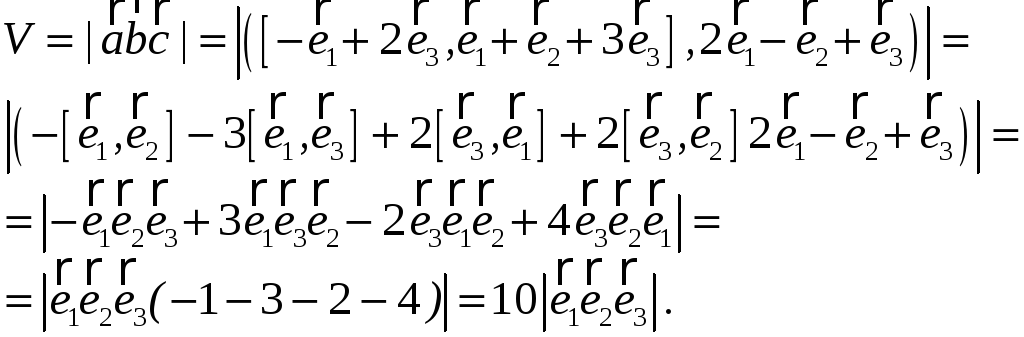
 ;
;
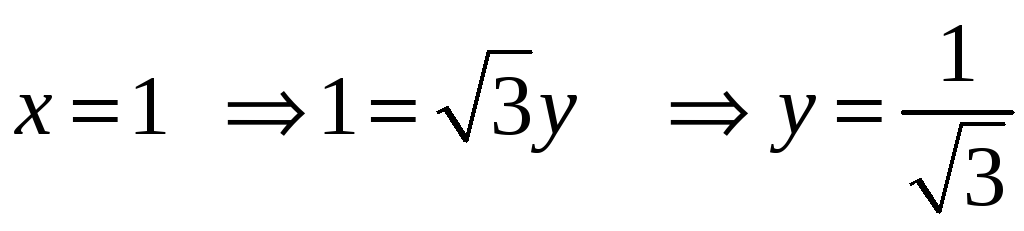 .
.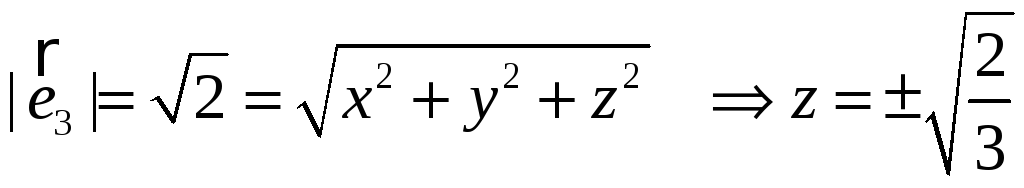 .
Тогда
.
Тогда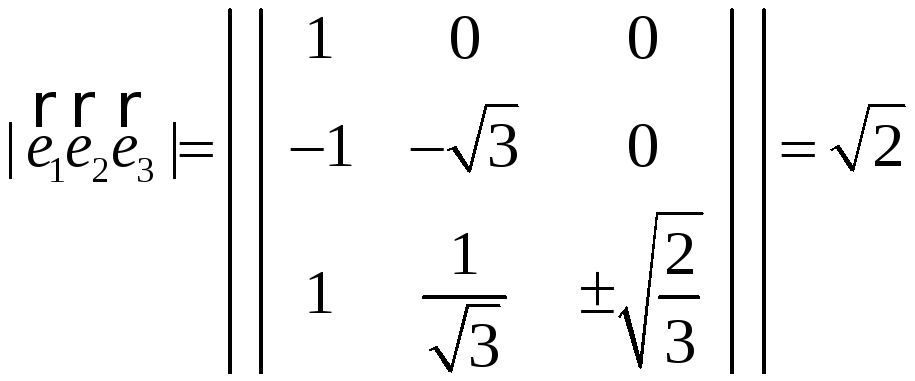 ,
,
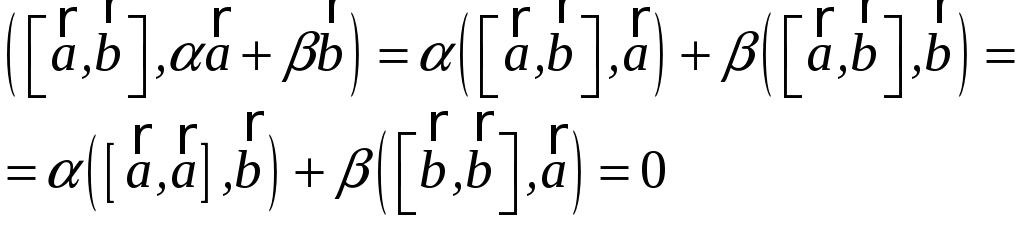 .
.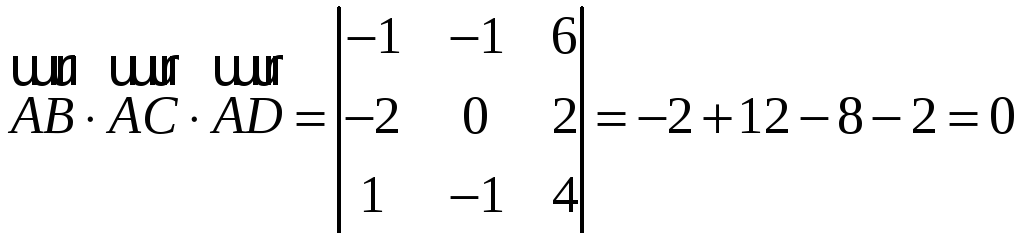 ,
что
и требовалось доказать.
,
что
и требовалось доказать.