
- •Оглавление
- •3. Прямая линия в пространстве 22
- •4. Прямая и плоскость 25
- •1. Простейшие задачи на плоскости 26
- •I. Векторная алгебра
- •1. Определение вектора
- •2. Линейные операции над векторами и их свойства
- •3. Базис и координаты Декартов прямоугольный базис и декартова система координат
- •Декартова прямоугольная система координат
- •Проекция вектора на ось
- •4. Скалярное произведение векторов
- •Геометрические приложения скалярного произведения векторов в декартовой системе координат
- •5. Векторное произведение векторов
- •6. Смешанное произведение векторов
- •Выражение смешанного произведения в декартовых координатах
- •II. Аналитическая геометрия в пространстве
- •1. Уравнения поверхностей и линий
- •2. Плоскость в пространстве
- •Общее уравнение плоскости (поверхность первого порядка)
- •Неполные уравнения плоскостей
- •Уравнение плоскости «в отрезках»
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Уравнение плоскости, проходящей через три данные точки
- •Угол между двумя плоскостями
- •Условие параллельности и перпендикулярности плоскостей
- •Уравнение прямой, проходящей через две данные точки
- •Угол между двумя прямыми
- •Условие параллельности и перпендикулярности двух прямых
- •4. Прямая и плоскость Точка пересечения прямой и плоскости
- •Уравнение пучка плоскостей, проходящих через прямую
- •III. Аналитическая геометрия на плоскости
- •2. Прямая линия на плоскости
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Окружность
- •Гипербола
- •Сопряженные гиперболы – две гиперболы, которые в одной и той же системе прямоугольных координат при одних и тех же значениях и определяются уравнениями и .
- •Парабола
- •4. Преобразования координат Параллельный перенос
- •Поворот координатных осей
- •Изменение начала координат и поворот осей
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •5. Линии в полярной системе координат
- •Связь полярных координат с декартовыми
- •Окружности
- •Спирали
- •Астроида
- •IV. ПоверхносТи второго порядка
- •Исследование формы поверхностей второго порядка по их каноническим уравнениям
- •Эллипсоид
- •Гиперболоиды Однополостный гиперболоид
- •Двуполостный гиперболоид
Декартова прямоугольная система координат
Декартова система
координат в пространстве определяется
заданием точки О – начала координат
и базисных векторов
![]() (трех взаимно перпендикулярных векторов
единичной длины).
(трех взаимно перпендикулярных векторов
единичной длины).
Вектор
![]() ,
идущий из начала координат в точку
,
идущий из начала координат в точку
![]() ,
называется радиус-вектором точки
,
называется радиус-вектором точки
![]() .
.
Координаты
радиус-вектора
![]() и координаты точки
и координаты точки
![]() совпадают
совпадают
![]() .
.
Е сли
известны координаты точек начала
сли
известны координаты точек начала
![]() и конца
и конца
![]() вектора, то координаты вектора
вектора, то координаты вектора
![]() .
.
Два вектора равны, тогда и только тогда, когда равны их соответствующие координаты в одном и том же базисе.
Необходимым и достаточным
условием коллинеарности векторов
![]() и
и
![]() ,
,
![]() ,
является пропорциональность их
соответствующих координат:
,
является пропорциональность их
соответствующих координат:
![]()
Линейные операции над
векторами сводятся к линейным операциям
над их координатами:
![]() ,
,
![]() .
.
Проекция вектора на ось
Осью называется прямая с лежащим
на ней единичным вектором
![]() (ортом), задающим положительное
направление на прямой.
(ортом), задающим положительное
направление на прямой.
Проекцией
![]() вектора
вектора
![]() на ось называется направленный отрезок
на оси, алгебраическое значение которого
равно скалярному произведению
на ось называется направленный отрезок
на оси, алгебраическое значение которого
равно скалярному произведению
![]() .
.
Для вектора
![]() проекция
на прямую
проекция
на прямую
![]() равна числу
равна числу
![]() .
.
Проекции обладают свойствами:
1)
![]() ;
;
2)
![]() .
.
Декартовы
прямоугольные координаты вектора
![]() равны проекциям этого вектора на оси
равны проекциям этого вектора на оси
![]() ,
,
![]() ,
,
![]() соответственно:
соответственно:
![]() ,
,
![]() ,
,
![]() ,где
,где
![]() – углы, которые составляет вектор
– углы, которые составляет вектор
![]() с координатными осями
с координатными осями
![]() ,
,
![]() ,
,
![]() .
.
Косинусы
углов (![]() ,
,
![]() ,
,
![]() )
вектора
)
вектора
![]() с векторами базиса
с векторами базиса
![]() называются направляющими косинусами
вектора
называются направляющими косинусами
вектора
![]() .
.
Вектор
 представляет собой вектор единичной
длины в направлении вектора
представляет собой вектор единичной
длины в направлении вектора
![]() .
.
4. Скалярное произведение векторов
Скалярным произведением
![]() ненулевых векторов
ненулевых векторов
![]() называется число, равное произведению
длин этих векторов на косинус угла
называется число, равное произведению
длин этих векторов на косинус угла
![]() между ними:
между ними:
![]() ,
,
![]() .
.
Скалярное произведение обладает свойствами:
-
 ;
; -
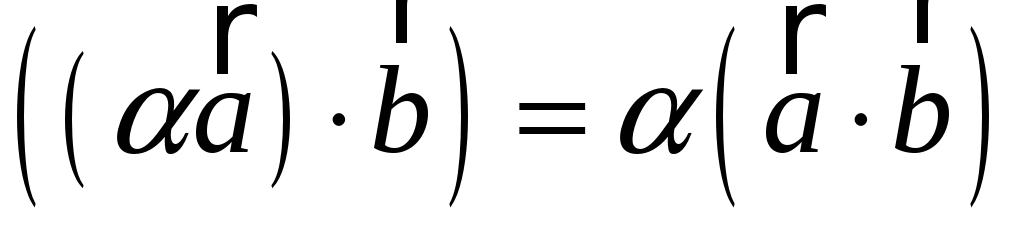 ;
; -
 ;
; -
 ,
если
,
если
 ;
;
-
 ,
если
,
если
 или (и)
или (и)
 или
или
 .
.
Выражение скалярного произведения векторов в декартовых координатах
Теорема. Если два
вектора
![]() и
и
![]() определены своими декартовыми
прямоугольными координатами
определены своими декартовыми
прямоугольными координатами
![]() ,
,
![]() ,
то скалярное произведение этих векторов
равно сумме произведений их соответствующих
координат, то есть
,
то скалярное произведение этих векторов
равно сумме произведений их соответствующих
координат, то есть
![]() .
.
Доказательство.
![]()
![]() Но
Но
![]() ,
аналогично
,
аналогично
![]() ,
,
![]() ;
;
![]()
![]() .
.
Геометрические приложения скалярного произведения векторов в декартовой системе координат
-
 =
=
 .
. -
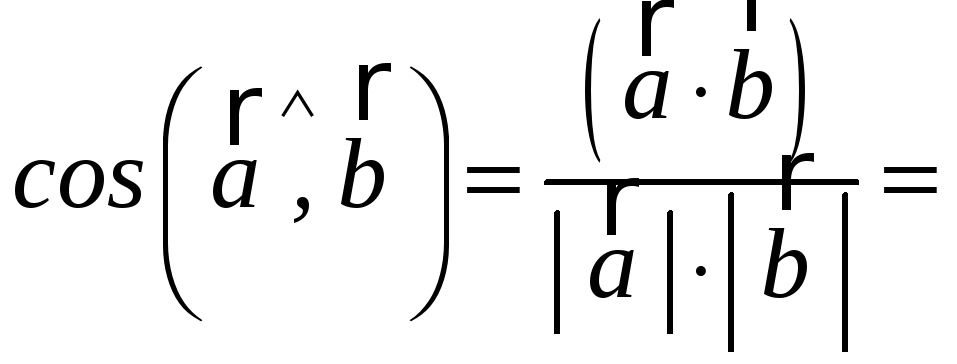
 .
. -
Проекция
 вектора
вектора
 на вектор
на вектор

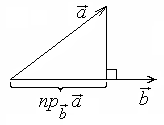
 .
.
-
Направляющие косинусы вектора
 :
:
 ,
,
 ,
,
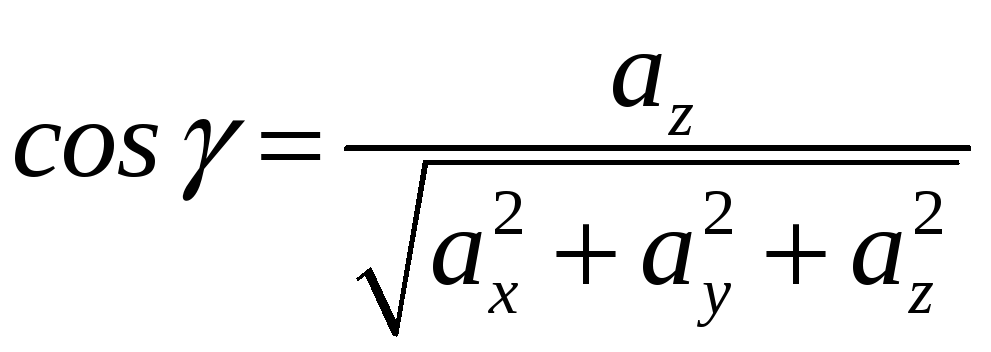 .
.
-
Для направляющих косинусов справедливо соотношение
![]() .
.
5. Векторное произведение векторов
В
пространстве различают правые и левые
тройки векторов. Упорядоченная
тройка некомпланарных векторов
![]() ,
,![]() ,
,![]() приведенных к одному началу, называется
правой,
если из конца третьего вектора
приведенных к одному началу, называется
правой,
если из конца третьего вектора
![]() кратчайший поворот первого вектора
кратчайший поворот первого вектора
![]() ко второму
ко второму
![]() виден совершаемым против часовой
стрелки. В противном случае тройка
называется левой.
виден совершаемым против часовой
стрелки. В противном случае тройка
называется левой.
-

правая

левая
Тройка
векторов базиса
![]() считается правой.
считается правой.
При перестановке местами двух соседних векторов ориентация тройки меняется.
Если
тройки
![]() - правые, то
- правые, то
![]() - левые.
- левые.
При круговой (циклической) перестановке векторов ориентация тройки
не меняется.
Векторным произведением
![]() ненулевых и неколлинеарных векторов
ненулевых и неколлинеарных векторов
![]() и
и
![]() называется вектор
называется вектор
![]() ,
удовлетворяющий следующим трем
требованиям:
,
удовлетворяющий следующим трем
требованиям:
1) длина вектора
![]() равна произведению длин векторов
равна произведению длин векторов
![]() и
и
![]() на синус угла между ними, т.е.
на синус угла между ними, т.е.![]() ,
,
2) вектор
![]() ортогонален к каждому из векторов
ортогонален к каждому из векторов
![]() и
и
![]() ,
т.е.
,
т.е.
![]() перпендикулярен плоскости, в которой
лежат векторы
перпендикулярен плоскости, в которой
лежат векторы
![]() и
и
![]() .
.
3). Вектор
![]() направлен так, что тройка
направлен так, что тройка
![]()
![]()
![]() является правой.
является правой.
Векторное произведение полагают
равным нулю, если
![]() или (и)
или (и)
![]() или они коллинеарны.
или они коллинеарны.
Векторное произведение обладает свойствами:
-
 ;
;
-
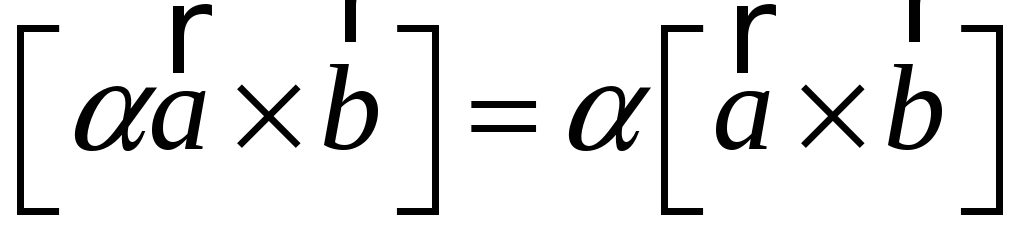 ;
; -
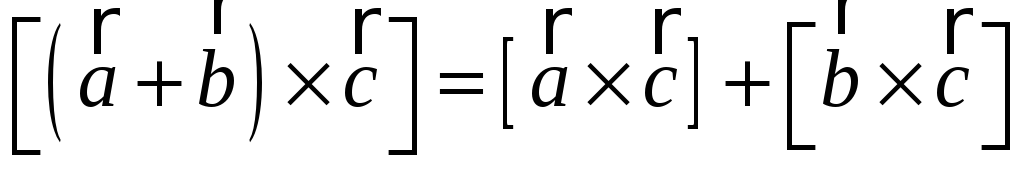 ;
; -
 для любого вектора
для любого вектора
 .
. -
 ,
если векторы
,
если векторы
 и
и
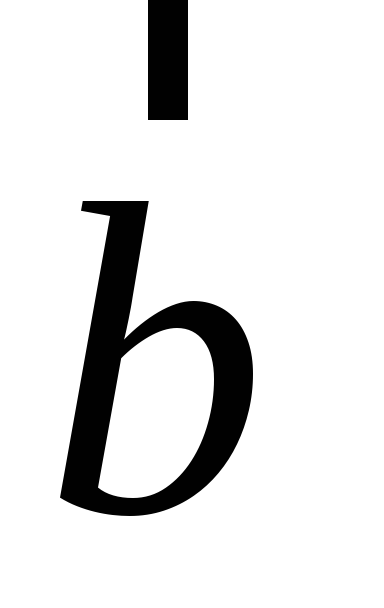 коллинеарны.
коллинеарны.
Приведем некоторые схемы для
вычисления различных векторных
произведений векторов базиса
![]() :
:

![]()
![]() ,
,
![]() .
.
Выражение векторного произведения векторов в декартовых координатах
Теорема. Если два
вектора
![]() и
и
![]() заданы своими декартовыми прямоугольными
координатами
заданы своими декартовыми прямоугольными
координатами
![]() ,
,
![]() ,
то
,
то
 .
.
Доказательство.
![]()
![]()
![]() .
.
Если записать
векторное произведение в виде определителя
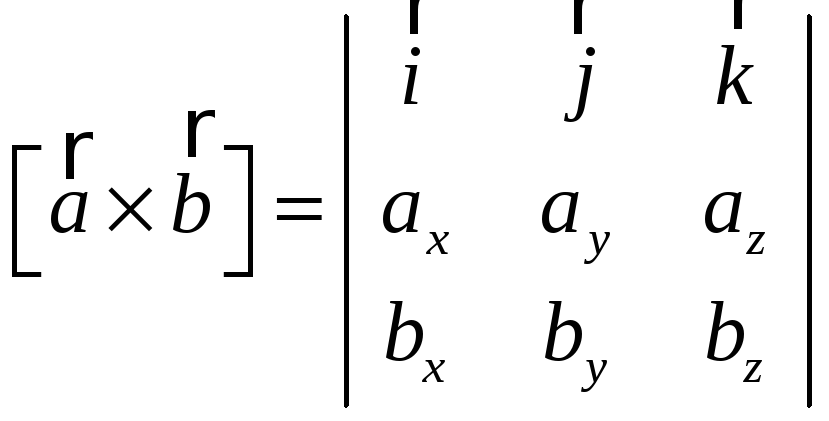 ,
,
то его координаты получаются при разложении определителя по элементам первой строки.
Теорема. Модуль
вектора
![]() равен площади
равен площади
![]() параллелограмма, построенного на
векторах
параллелограмма, построенного на
векторах
![]() и
и
![]() .
.
Доказательство.
Площадь
параллелограмма (см. рис.), построенного
на векторах
![]() и
и
![]() ,
равна
,
равна
![]() .
.
