Астроида

Астроидой называется кривая, которую описывает точка окружности радиуса R/4, когда окружность катится без скольжения внутри окружности радиуса R.

Параметрические уравнения астроиды

где

В декартовых координатах уравнение астроиды

x^2/3+y^2/3=R^2/3.

Длина астроиды L=6R, а площадь, ограниченная астроидой S=3R²/8.

IV. ПоверхносТи второго порядка

Алгебраической поверхностью второго порядка называется поверхность, уравнение которой в декартовой системе координат имеет вид:

Ax²+By²+Cz²+2Dxy+2Exz+2Fyz+gx+Hy+Iz+K=0,

где не все коэффициенты при членах второго порядка равны одновременно нулю (в противном случае получаем алгебраическую поверхность первого порядка, т.е. плоскость).

В зависимости от значений коэффициентов возможны случаи, когда уравнение определяет вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей).

Например, уравнение не имеет решений и задает пустое множество, уравнение задает точку с координатами (0,0,0), уравнение задает плоскость х = 1, уравнение задает пару плоскостей х = у и х = у.

Исследование формы поверхностей второго порядка по их каноническим уравнениям

Основным методом исследования формы поверхности по ее уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями

Эллипсоид

Эллипсоидом называется поверхность второго порядка с каноническим уравнением

.

Рассмотрим сечение эллипсоида плоскостью . Линия пересечения эллипсоида и плоскости задается системой уравнений

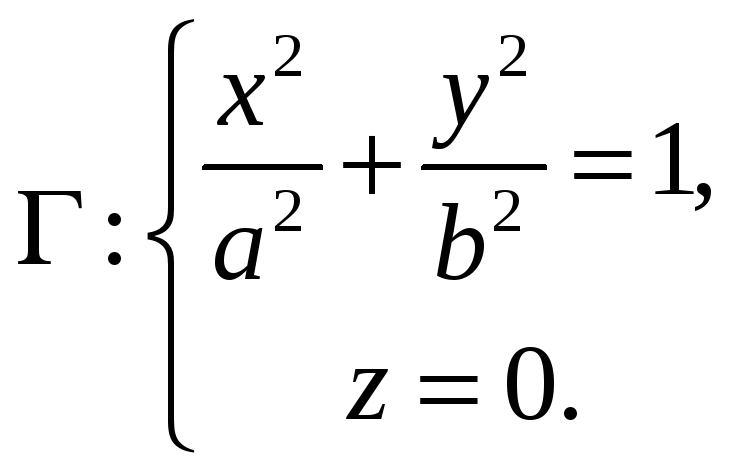
Г – эллипс с полуосями а и b в плоскости .

Рассмотрим сечение эллипсоида плоскостью . Линия пересечения задается системой уравнений

где Таким образом, если , то Г – эллипс с полуосями в плоскости Если , Г – точка с координатами Если , система решений не имеет, т.е. исследуемая поверхность не имеет общих точек с рассматриваемой плоскостью.

Далее, так как переменная z содержится в уравнении во второй степени, плоскость является плоскостью симметрии эллипсоида. Отсюда следует, что достаточно исследовать форму поверхности и построить ее часть в области , достроив затем остальную часть путем зеркального отражения найденного фрагмента поверхности относительно координатной плоскости ОXY.

Аналогично рассматриваются сечения поверхности плоскостями

Эллипсоид - замкнутая овальная поверхность, имеющая три плоскости симметрии:

Если , каноническое уравнение эллипсоида принимает вид . При этом линиями пересечения эллипсоида с плоскостями , где –с < h < c, являются окружности, центры которых лежат на оси OZ и, следовательно, в этом случае эллипсоид является фигурой вращения с осью OZ.

Если , каноническое уравнение принимает вид

и задает сферу с центром в начале координат и радиусом R.

Гиперболоиды Однополостный гиперболоид

Однополостным гиперболоидом называется поверхность второго порядка с каноническим уравнением

.

Линия пересечения гиперболоида и плоскости задается системой уравнений

и определяет эллипс с полуосями а и b.

В сечении плоскостью получаем эллипс:

с большими, чем в предыдущем случае полуосями

Сечение поверхности плоскостью дает уравнение линии пересечения в виде:

и представляет гиперболу, пересекающую ось OY.

Сечение плоскостью задает гиперболу, пересекающую ось OX.

Однополостный гиперболоид - поверхность, имеющая вид расширяющейся трубки с тремя плоскостями симметрии