Лінійна алгебра

1. Математична довідка.

1. Визначник другого порядку

.

2. Розв’язання системи

дається :

1. формулами Крамера

де

,

2. методом виключення невідомих, наприклад, із другого рівняння

тоді перше рівняння буде з одним невідомим

.

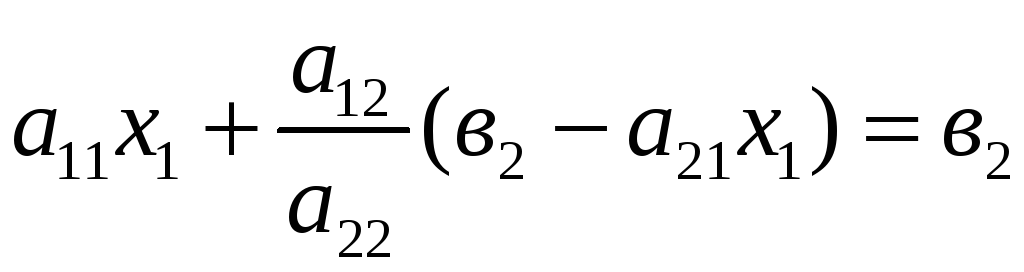3. Розв’язки однорідної системи

даються формулами

,

де ; ; 

мінори матриці

4. Визначник третього порядку

або

де ; ; 

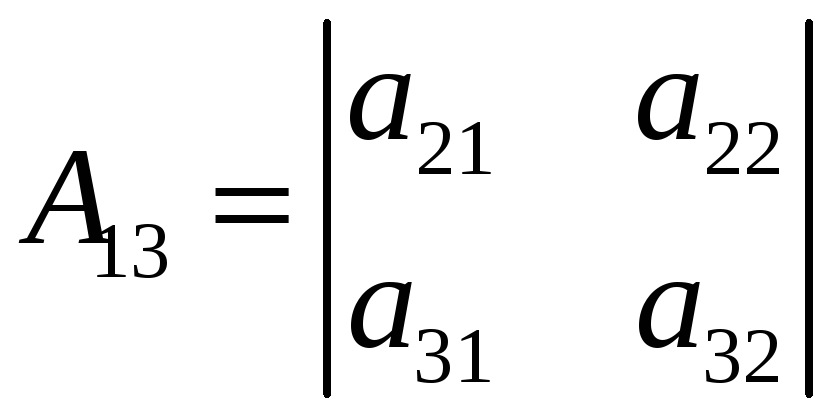
алгебраїчні доповнення відповідних елементів визначника.

5. Розв'язування системи

дається формулами Крамера

^, де

6. Розв’язання однорідної системи

якщо і

знаходиться із підсистеми

(див.п.3).

7. Систему п. 5 можна розв’язувати методом виключення невідомих, методом Гауса, матричним методом та ін.

2. Приклади розв’язування.

Приклад 1.1. Розв’язати по правилу Крамера систему рівнянь:

Розв’язання

Обчислимо визначник системи

Так як , то система має єдиний розв’язок. Використаємо формули Крамера _, ^.

Знаходимо:

Відповідь:

Приклад 1.2. Розв’язати методом Гауса систему рівнянь

Розв’язання

Залишимо перше рівняння системи без змін; до другого добавимо перше, помножене на –1, а до третього добавимо перше, помножене на –2:

Залишимо два перших рівняння без змін, а до третього добавимо друге, помножене на :

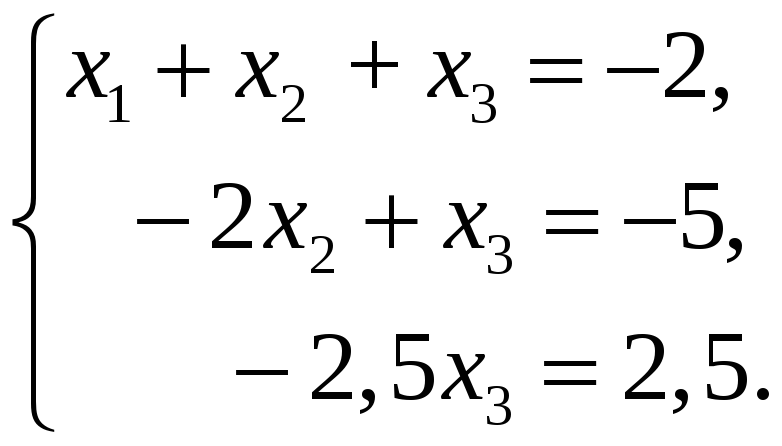
Кінець прямого ходу: одержали матрицю трикутної форми.

Обернений хід:

Із третього рівняння знаходимо ; підставимо його в друге, розв’язавши яке відносно , одержимо х₂ = 2. Значення х₃, х₂ підставимо в перше рівняння і, розв’язавши його відносно х₁, знайдемо х₁= -3.

Відповідь: х₁ = -3; х₂ = 2; х₃ = -1.

Приклад 1.3. Розв’язати методом Гауса систему рівнянь

Розв’язання

Переставимо місцями перше та друге рівняння:

Перше рівняння системи залишимо без змін; до другого добавимо перше, помножене на –2, а до третього – перше, помножене на –1:

Друге і третє рівняння однакові, одне з них можна опустити:

В цій системі три невідомих, а рівнянь два, тому одне з невідомих являється вільним. Вважаючи вільним невідоме х₃, перепишемо систему так:

Із другого рівняння системи знайдемо:

.

Підставимо знайдене х₂ в перше рівняння, знайдемо

.

Відповідь: .

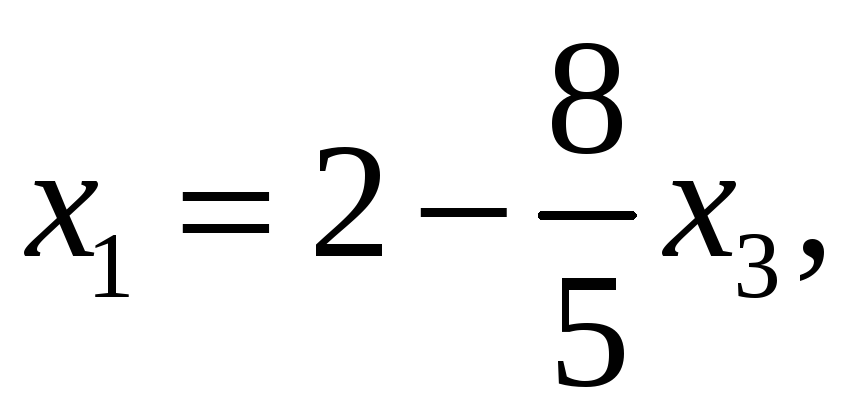
Приклад 1.4. Розв’язати з допомогою оберненої матриці систему рівнянь

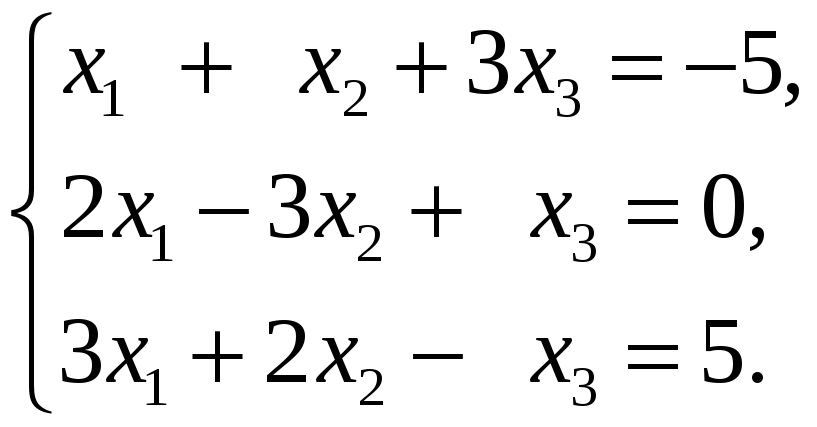
Розв’язання

Запишемо систему рівнянь в матричній формі

АХ = В.

Помножимо обидві частини рівняння АХ = В на А^-1 зліва, тобто

А^-1АХ = А^-1В або Х = А^-1В.

Таким чином, для розв’язку потрібно побудувати матрицю А^-1, обернену до матриці А.

В нас

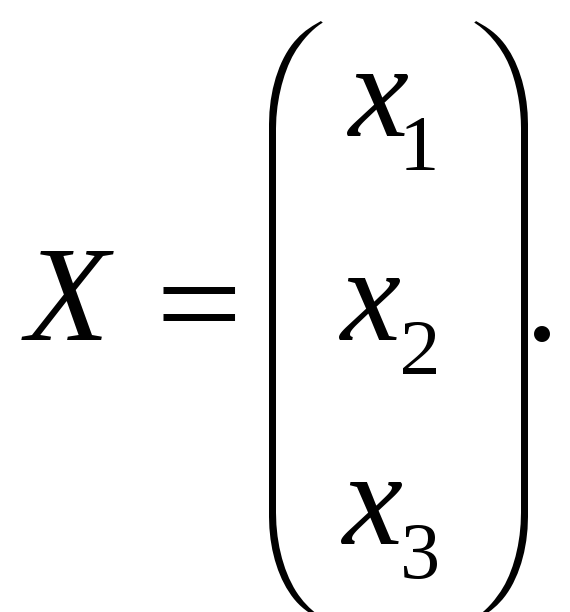
Обернену матрицю знаходимо по формулі:

де

- транспонована матриця ;

- приєднана до А матриця, складена з алгебраїчних доповнень елементів матриці А.

Обчислюємо

Обчислюємо алгебраїчні доповнення до елементів матриці А:

,

,

,

,

,

,

,

,

.

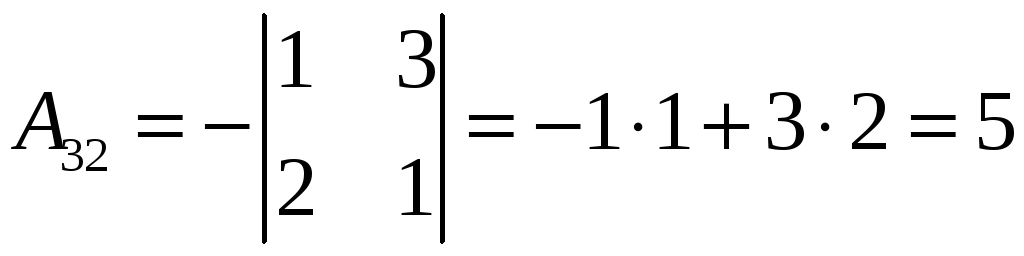Складаємо матрицю :

Транспонуємо :

Отримуємо обернену матрицю:

Тоді

Відповідь:

Приклад 1.5. Розв’язати систему рівнянь

а) за методом Крамера;

б) за методом Гауса;

в) матричним методом.

Розв’язання

а) за методом Крамера:

Тоді

б) методом Гауса:

Складаємо розширену матрицю системи та приведемо її до трикутної за допомогою еквівалентних перетворень.

Від другого рядка матриці віднімемо перший рядок помножений на 2, а від третього рядка віднімемо перший помножений на 3:

Від третього рядка віднімемо другий помножений на 8:

Кінець прямого ходу.

Запишемо відповідну систему:

Обернений хід.

Із третього рівняння х₃ = 3.

З другого рівняння системи маємо

.

Із першого рівняння:

.

Отже, розв’язок системи:

.

в) Матричним методом:

Систему можна записати у матричному вигляді АХ = В, де:

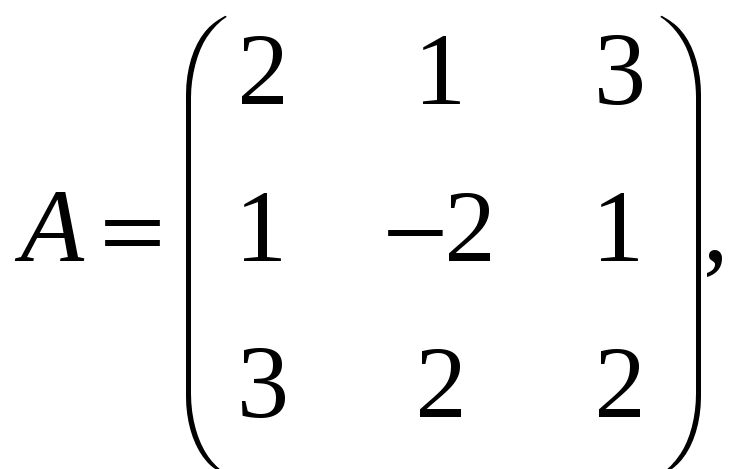
Тоді, якщо розв’язок системи знаходимо за формулою

Х = А^-1В.

Знайдемо матрицю А^-1, обернену до А.

Мали .

Обчислюємо алгебраїчні доповнення до елементів матриці А:

,

,

,

,

,

,

,

,

.

Складаємо:

Транспонуємо :

.

Знаходимо обернену матрицю:

.

Тоді

Таким чином, розв’язок системи