1. Описание логических переменных. Операции над ними

Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые лежат в основе работы компьютера.

Основоположником математической логики является великий немецкий математик Готфрид Вильгельм Лейбниц (1646 - 1716 гг.). Он сделал попытку построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычислений. На заложенном Лейбницем фундаменте ирландский математик Джордж Буль построил здание новой науки - математической логики, - которая в отличие от обычной алгебры оперирует не числами, а высказываниями. В честь Д.Буля логические переменные в языке программирования Паскаль впоследствии назвали булевыми.

Суждения в математической логике называются высказываниями или логическими выражениями.

Высказывание - это любое утверждение, относительно которого можно сказать (имеет смысл говорить) истинно оно или ложно. Вообще, существуют разные варианты обозначения истинности и ложности высказываний:

Истина	И	True	T	1
Ложь	Л	False	F	0

По своей сути высказывания фактически являются двоичными объектами и поэтому часто истинному значению высказывания ставят в соответствие 1, а ложному - 0. Например, запись А = 1 означает, что высказывание А истинно.

Высказывания могут быть простыми и сложными. В булевой алгебре простым высказываниям соответствуют алгебраические переменные, а сложным алгебраические функции. Функции могут получаться путем объединения переменных с помощью логических операций. Существует пять логических операций. Рассмотрим подробно каждую из них.

Логическое отрицание. Самой простой логической операцией является операция НЕ (по-другому ее часто называют отрицанием или инверсией и обозначают NOT А, или ­). Результат отрицания всегда противоположен значению переменной.

Например: А: «Тоска зеленая», тогда 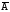: «Тоска НЕ зеленая» или «НЕВЕРНО, что Тоска зеленая»

Логическая операция НЕ является унарной, т.е. имеет всего одну переменную. Все остальные операции являются бинарными, так как представляют собой результаты действий над двумя логическими величинами. Определение отрицания может быть записано с помощью таблицы истинности:

А	¬ А
И	Л
Л	И

Логическое умножение. Логическая операция И соответствует логическому умножению ( по другому ее называют конъюнкция и обозначают АAND В, АВ или А&В).

Например: Сложное высказывание «Для остановки ОС «Windows'95» требуется процессор не ниже 80386 и не менее 4 Мбайт оперативной памяти» представляет собой конъюнкцию двух простых высказываний А: «Для остановки ОС «Windows'95» требуется процессор не ниже 80386» и В: «Для остановки ОС «Windows'95» требуется процессор не менее 4 Мбайт оперативной памяти». Очевидно, что данное сложное высказывание будет истинно тогда и только тогда, когда будут истинны оба простых высказывания (это значит, что установка ОС «Windows'95» будет успешной только при одновременном выполнении обоих условий). Определение конъюнкции может быть записано с помощью таблицы истинности:

А	В	А&B
и	и	и
и	л	л
л	и	л
л	л	л

Логическое сложение. Логическая операция ИЛИ соответствует логическому сложению ( по другому ее называют дизъюнкция и обозначают АOR В, АВ).

Например: Сложное высказывание «Мел черный или доска черная» представляет собой дизъюнкцию двух простых высказываний А: «Мел черный» и В: «Доска черная». Очевидно, что данное сложное высказывание будет истинно тогда и только тогда, когда будет истинно хотя бы одно из простых высказываний. Определение дизъюнкции может быть записано с помощью таблицы истинности:

А	В	АVB
И И Л Л	И Л И Л	И И И Л

Логическое следование. Логическая операция ЕСЛИ…,ТО соответствует логическому следованию ( по другому ее называют импликация и обозначают А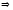В или АВ).

Например: Сложное высказывание «Если идет дождь, то видимость на дороге ухудшается» представляет собой импликацию двух простых высказываний А: «Идет дождь» и В: «Видимость на дороге ухудшается». Импликация ложна тогда и только тогда, когда А истинно, а В ложно. Во всех остальных случаях импликация истинна. Определение импликации может быть записано с помощью таблицы истинности:

А	В	А=>В
И И Л Л	И Л И Л	И Л И И

Логическое тождество. Логическая операция ТОГДА И ТОЛЬКО ТОГДА, КОГДА соответствует логическому тождеству( по другому ее называют эквивалентностью или двойной импликацией и обозначают АВ или АВ).

Например: Сложное высказывание «Железо легкое тогда и только тогда, когда пух тяжелый» представляет собой эквивалентность двух простых высказываний А: «Железо легкое» и В: «Пух тяжелый». Очевидно, что данное сложное высказывание будет истинно тогда и только тогда, когда оба простых высказывания будут одновременно истинны или ложны. Определение эквивалентности может быть записано с помощью таблицы истинности:

А	В	А<=>В
И И Л Л	И Л И Л	И Л Л И

Приведем примеры записи сложных высказываний с помощью обозначения логических операций:

 "Быть иль не быть - вот в чем вопрос." (В. Шекспир) А V ¬ A <=> В  "Если хочешь быть красивым, поступи в гусары." (К. Прутков) А =>В

В таблицах истинности указываются все возможные комбинации логических переменных, а также соответствующие им результаты операций. Таблица истинности может рассматриваться в качестве одного из способов задания логической функции.