
- •Экономический факультет Кафедра экономической информатики в.С. Громницкий
- •Часть I. Линейное программирование 9
- •Часть II. Методы нелинейной оптимизации 81 Введение
- •Задачи принятия решений
- •Математическое моделирование
- •Часть I. Линейное программирование Глава 1. Линейные математические модели в экономических исследованиях
- •1.1. Экономические задачи
- •Задача объемного планирования
- •Задача о диете
- •1.2. Общий вид математической модели задачи линейного программирования
- •1.3. Различные формы задач линейного программирования
- •Приведение задачи линейного программирования от одной эквивалентной формы к другой
- •Примеры решения задач
- •1.4. Графическое решение задач
- •Свойства области допустимых решений
- •Глава 2. Математические свойства задачи линейного программирования
- •2.1. Свойства области допустимых решений
- •2.2. Базисные и опорные решения
- •Глава 3. Симплекс-метод решения задачи линейного программирования
- •3.1. Идея симплекс-метода
- •3.2. Векторное представление симплексных преобразований
- •3.3. Симплекс-метод в уравнениях
- •3.4. Симплекс-метод в таблицах
- •Правила построения симплекс-таблиц
- •Этапы симплекс-метода
- •3.5. Варианты разрешимости задачи линейного программирования
- •3.6. Предупреждение зацикливания симплекс-метода
- •Глава 4. Метод искусственного базиса
- •4.1. Построение начального опорного плана
- •Пример построения начального опорного плана
- •4.2. Решение задачи линейного программирования методом искусственного базиса
- •Пример решения задачи методом искусственного базиса
- •Глава 5. Теория двойственности в задачах линейного программирования
- •5.1. Построение двойственной задачи и ее экономическая интерпретация
- •Математическая формулировка двойственной задачи к произвольной задаче линейного программирования
- •Правила построения двойственной задачи
- •5.2. Математические свойства пары взаимно двойственных задач
- •Варианты разрешимости задач двойственной пары
- •Вторая теорема двойственности
- •5.3. Анализ чувствительности оптимального решения к изменению свободных членов ограничений
- •5.4. Определение оптимального решения двойственной задачи из оптимальной симплекс-таблицы прямой
- •5.5. Двойственный симплексный метод
- •Глава 6. Послеоптимизационный анализ задачи линейного программирования
- •6.1. Добавление нового ограничения
- •6.2. Добавление новой переменной
- •6.3. Изменение коэффициентов критерия
- •Изменение коэффициента критерия при свободной переменной
- •Изменение коэффициента критерия при базисной переменной
- •6.4. Изменение технологических коэффициентов
- •Изменение технологических коэффициентов при базисной переменной
- •Изменение технологических коэффициентов при свободной переменной
- •Часть II. Методы нелинейной оптимизации
- •Глава 7. Классическая теория оптимизации
- •7 (3) .1. Необходимые условия оптимальности
- •7.2. Достаточные условия оптимальности
- •Глава 8. Нелинейное программирование
- •8.1. Задачи на условный экстремум. Метод множителей Лагранжа.
- •8.2. Задачи выпуклого программирования
- •8.3. Задачи квадратичного программирования
- •Задания к лабораторным работам Лабораторная работа 1. Свойства области допустимых решений задачи линейного программирования
- •Лабораторная работа 2. Симплекс-метод. Варианты разрешимости задачи линейного программирования
- •Лабораторная работа 3. Теория двойственности в задачах линейного программирования
- •Лабораторная работа 4. Послеоптимизационный анализ задач линейного программирования
- •Перечень задач к лабораторным работам 3 и 4
- •Литература
8.2. Задачи выпуклого программирования
Пусть исходная задача имеет вид:
(11) (12) (13)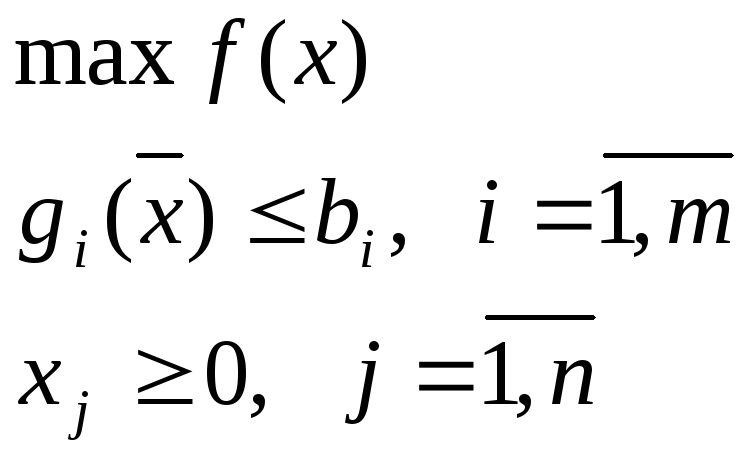
Задача (11-13) называется задачей выпуклого программирования, если выполняются следующие условия:
-
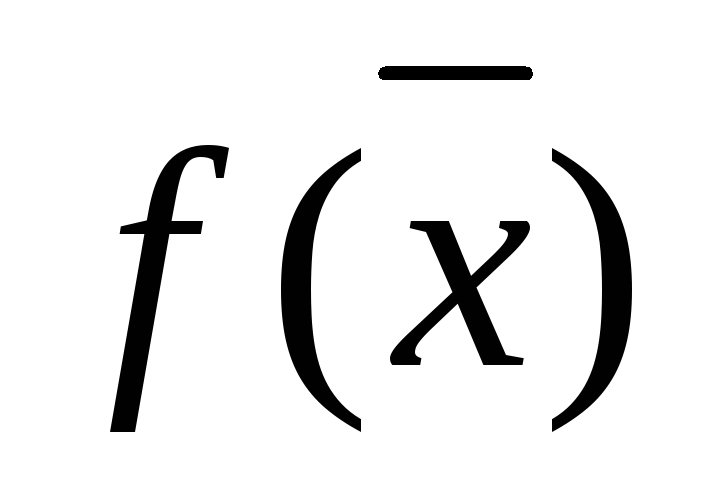 –
вогнутая функция,
то есть для
–
вогнутая функция,
то есть для
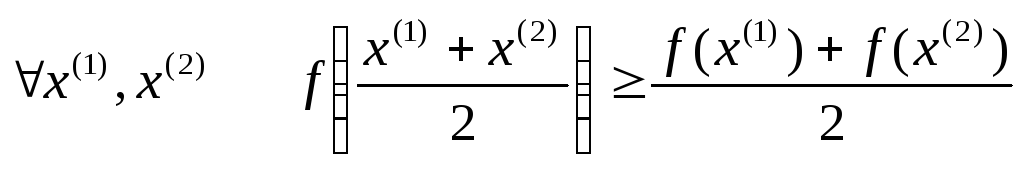 .
. -
Область допустимых решений
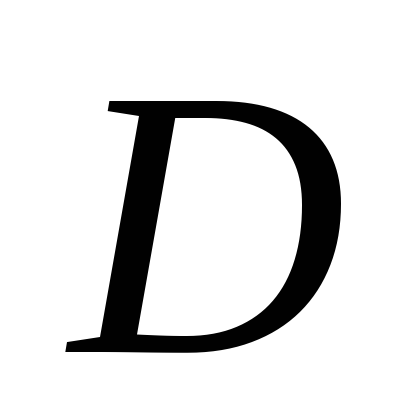 выпуклая.
выпуклая. -
Область регулярная, то есть существует по крайней мере одна внутренняя точка
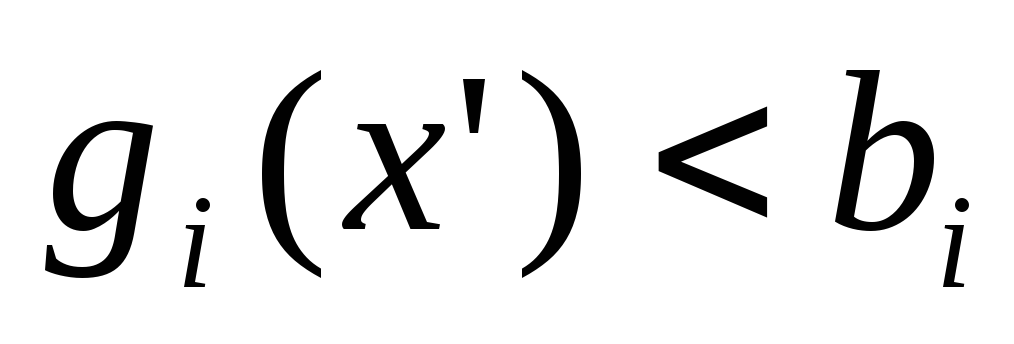 .
.
Можно построить функцию Лагранжа
![]()
Теорема
8: точка
![]() является оптимальным решением задачи
выпуклого программирования тогда и
только тогда, когда существует вектор
является оптимальным решением задачи
выпуклого программирования тогда и
только тогда, когда существует вектор
![]() такой, что для функции Лагранжа выполняются
условия
такой, что для функции Лагранжа выполняются
условия
-
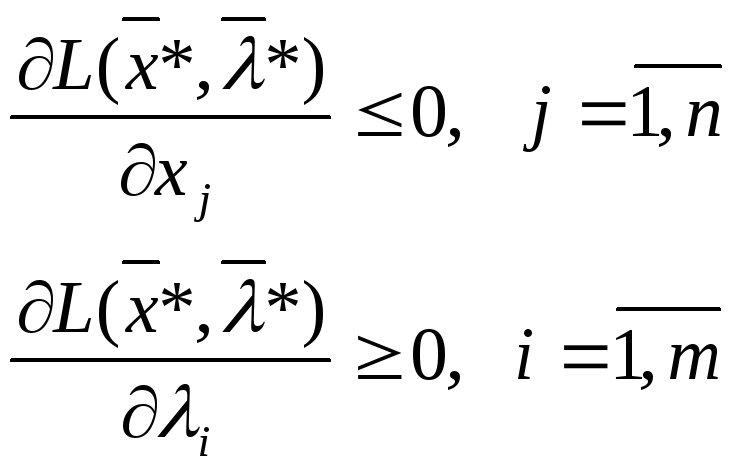
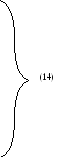
-
условия дополняющей нежесткости:
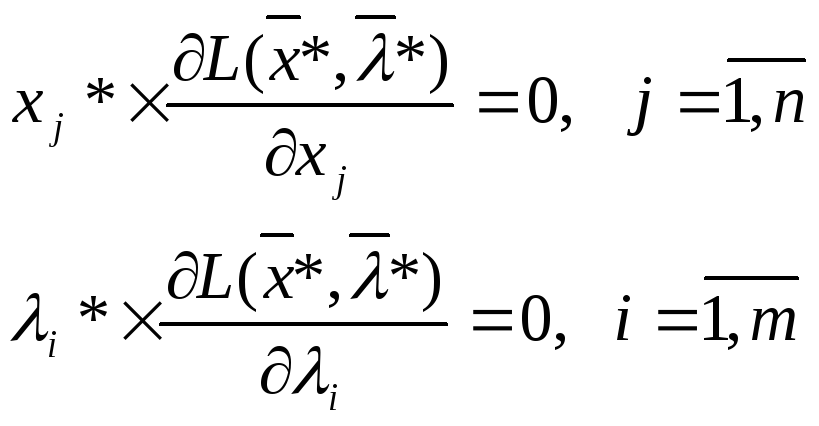
Условия (14) называются
условиями
Куна-Таккера, а
точка
![]() – точкой
Куна-Таккера
– точкой
Куна-Таккера
Рассмотрим геометрический смысл условий Куна-Таккера.
Из первого условия
(14.2) следует, что если все
![]() ,
,
![]() ,
то
,
то
![]()
Второе условие
(14.2), так как
![]() ,
запишется в виде
,
запишется в виде
![]()
![]() и означает, что для неактивных ограничений
и означает, что для неактивных ограничений
![]() .
.
Тогда из условий дополняющей нежесткости следует
![]() (15)
(15)
![]()
то
есть градиент функции
![]() в оптимальной точке является линейной
комбинацией с положительными коэффициентами
градиентов к активным ограничениям.
Иными словами, градиент критерия лежит
в геометрическом конусе градиентов
ограничений.
в оптимальной точке является линейной
комбинацией с положительными коэффициентами
градиентов к активным ограничениям.
Иными словами, градиент критерия лежит
в геометрическом конусе градиентов
ограничений.
Если в оптимальной
точке какая-либо координата
![]() ,
то вместо градиентов функций
,
то вместо градиентов функций
![]() и
и
![]() рассматриваются их проекции на плоскость,
перпендикулярную оси j.
рассматриваются их проекции на плоскость,
перпендикулярную оси j.
В общем случае система уравнений и неравенств (14) слишком сложна для аналитического решения. Однако в задачах квадратичного программирования есть способы решения этой системы условий, сводящиеся к нахождению опорных решений систем линейных алгебраических уравнений.
8.3. Задачи квадратичного программирования
Пусть
![]() –
квадратичная функция,
–
квадратичная функция,
![]() –
линейные функции. Тогда задача выпуклого
программирования (11-13)
называется задачей квадратичного
программирования.
–
линейные функции. Тогда задача выпуклого
программирования (11-13)
называется задачей квадратичного
программирования.
Неравенства (14.1)
преобразуем в уравнения введением
дополнительных переменных
![]() и
и
![]() ,
тогда необходимые и достаточные условия
оптимальности (условия Куна-Таккера)
запишутся в виде
,
тогда необходимые и достаточные условия
оптимальности (условия Куна-Таккера)
запишутся в виде
(16)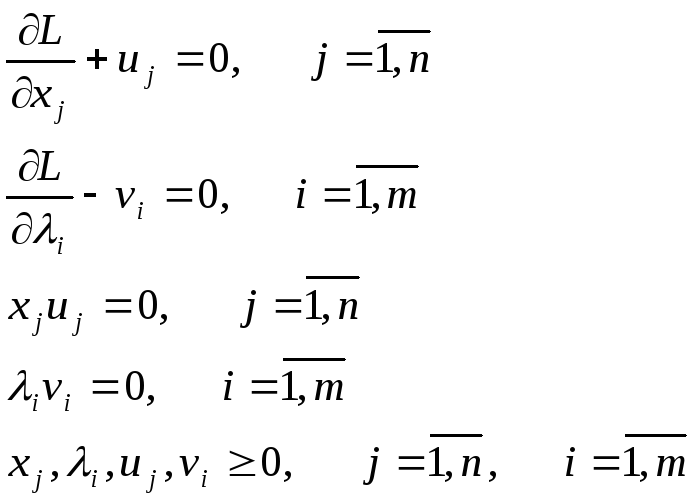
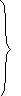
(16.1-16.2) –
это система линейных алгебраических
уравнений относительно неизвестных
![]() .
Опорное решение
этой системы уравнений может быть
найдено с помощью метода искусственного
базиса с дополнительными требованиями
(16.3-16.4). То есть, при введении переменных
в базис необходимо следить за тем, чтобы
.
Опорное решение
этой системы уравнений может быть
найдено с помощью метода искусственного
базиса с дополнительными требованиями
(16.3-16.4). То есть, при введении переменных
в базис необходимо следить за тем, чтобы
![]() ,
,![]() и
и
![]() ,
,![]() одновременно
не являлись базисными (так как базисные
переменные для невырожденного опорного
плана положительны).
одновременно
не являлись базисными (так как базисные
переменные для невырожденного опорного
плана положительны).
Два вектора условий
системы уравнений (16.1-16.2) назовем
сопряженными, если они либо соответствуют
неизвестным
![]() ,
,![]() при некотором j,
либо неизвестным
при некотором j,
либо неизвестным
![]() ,
,![]() при некотором i.
при некотором i.
Тогда для решения системы (16) достаточно найти опорное решение системы (16.1-16.2), базис которого не содержит сопряженных векторов условий.
Пример: Для производства 2-х видов продукции используется 2 ресурса, запасы которых составляют 8 и 12 тонн, а нормы расхода ресурсов на единицу (м3) продукции первого вида составляют соответственно 1 и 3 тонны, второго вида продукции – по 2 тонны.
Прибыль от реализации продукции зависит от объема продукции. Прибыль от реализации единицы продукции первого вида в объеме x1 м3 составляет 6-х1 тыс. руб. Прибыль от реализации единицы продукции второго вида в объеме х2 м3 составляет 10-х2 тыс. руб.
Определить план производства, максимизирующий суммарную прибыль от реализации всей произведенной продукции.
Математическая модель задачи
![]()
![]() (17)
(17)
![]()
![]()
![]()
Целевая функция
задачи
![]() вогнута, так как квадратичная форма
вогнута, так как квадратичная форма
![]() отрицательно определена (она всегда
отрицательно определена (она всегда
![]() ).
Об этом также свидетельствует отрицательная
определенность матрицы Гессе
).
Об этом также свидетельствует отрицательная
определенность матрицы Гессе
![]()
![]()
Её главные миноры принимают значения -2, 4, то есть знаки чередуются.
Область, задаваемая линейными ограничениями, выпукла, содержит внутренние точки. Значит задача (17) является задачей выпуклого (квадратичного) программирования.
Строим функцию Лагранжа
![]()
Условия оптимальности Куна-Таккера
1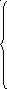 .
.
![]()
![]()
(18)![]()
![]()
![]()
![]()
![]()
![]()
2. Условия дополняющей нежесткости
![]()
![]()
![]()
![]() (19)
(19)
![]()
![]()
![]()
![]()
3.
![]() (20)
(20)
![]()
Приведем (18) к виду равенств введением дополнительных неотрицательных переменных u1, u2, v1, v2.
![]()
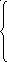
![]()
![]()
![]()
![]()
![]()
![]() (21)
(21)
![]()
![]()
![]()
![]()
![]()
Тогда условия дополняющей нежесткости (19) запишутся
![]()
![]() (22)
(22)
![]()
![]()
К условию (20) добавим требование неотрицательности дополнительных переменных
![]()
![]()
![]()
![]() (23)
(23)
Таким образом, для определения оптимального решения задачи (17) необходимо найти допустимое решение системы (21) с дополнительными условиями (22-23). В качестве допустимого достаточно найти опорное решение системы (21).
Опорное решение
будем искать методом искусственного
базиса. Для этого вводим в систему
уравнений (21) две искусственные переменные
![]() ,
,
![]() и минимизируем их сумму
и минимизируем их сумму
![]() (24)
(24)
![]()
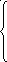
![]()
![]()
(25)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (26)
(26)
Решаем задачу
(24-26) симплекс-методом, следя за тем,
чтобы базис каждого опорного плана не
содержал сопряженных векторов условий.
То есть, одновременно не могут быть
базисными переменные из каждого условия
дополняющей нежесткости (22)
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Первая симплекс таблица будет иметь следующий вид
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
Сb |
Б.п |
x1 |
x2 |
|
|
u1 |
u2 |
v1 |
v2 |
y1 |
y2 |
b |
|
1 |
y1 |
2 |
0 |
1 |
3 |
-1 |
0 |
0 |
0 |
1 |
0 |
6 |
|
1 |
y2 |
0 |
2 |
2 |
2 |
0 |
-1 |
0 |
0 |
0 |
1 |
10 |
|
0 |
v1 |
1 |
2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
8 |
|
0 |
v2 |
3 |
2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
12 |
|
|
z |
2 |
2 |
3 |
5 |
-1 |
-1 |
0 |
0 |
0 |
0 |
16 |
Переменные
![]() ,
,
![]() нельзя вводить в список базисных, так
как вектора условий при v1,
нельзя вводить в список базисных, так
как вектора условий при v1,
![]() и v2,
и v2,
![]() сопряжены. Переменные x1,
x2
– можно. Выберем разрешающий столбец
при переменной x2.
Тогда разрешающая строка должна быть
третьей. После выполнения операции
однократного замещения получим следующую
симплекс-таблицу
сопряжены. Переменные x1,
x2
– можно. Выберем разрешающий столбец
при переменной x2.
Тогда разрешающая строка должна быть
третьей. После выполнения операции
однократного замещения получим следующую
симплекс-таблицу
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
Сb |
Б.п |
x1 |
x2 |
|
|
u1 |
u2 |
v1 |
v2 |
y1 |
y2 |
b |
|
1 |
y1 |
2 |
0 |
1 |
3 |
-1 |
0 |
0 |
0 |
1 |
0 |
6 |
|
1 |
y2 |
-1 |
0 |
2 |
2 |
0 |
-1 |
-1 |
0 |
0 |
1 |
2 |
|
0 |
x2 |
1/2 |
1 |
0 |
0 |
0 |
0 |
1/2 |
0 |
0 |
0 |
4 |
|
0 |
v2 |
2 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
4 |
|
|
z |
1 |
0 |
3 |
5 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
8 |
Теперь из трех
свободных переменных с положительными
оценками x1,
![]() ,
,
![]() нельзя вводить в список базисных
переменную
нельзя вводить в список базисных
переменную
![]() – переменные v2
и
– переменные v2
и
![]() одновременно окажутся базисными, будут
обе положительны и нарушится одно из
условий дополняющей нежесткости (22)
(вектора условий при v2
и
одновременно окажутся базисными, будут
обе положительны и нарушится одно из
условий дополняющей нежесткости (22)
(вектора условий при v2
и
![]() сопряжены).
Введем в список базисных переменную
сопряжены).
Введем в список базисных переменную
![]() .
Разрешающая строка вторая. Очередная
симплекс-таблица
.
Разрешающая строка вторая. Очередная
симплекс-таблица
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
Сb |
Б.п |
x1 |
x2 |
|
|
u1 |
u2 |
v1 |
v2 |
y1 |
y2 |
b |
|
1 |
y1 |
5/2 |
0 |
0 |
2 |
-1 |
1/2 |
1/2 |
0 |
1 |
-1/2 |
5 |
|
0 |
|
-1/2 |
0 |
1 |
1 |
0 |
-1/2 |
-1/2 |
0 |
0 |
1/2 |
1 |
|
0 |
x2 |
1/2 |
1 |
0 |
0 |
0 |
0 |
1/2 |
0 |
0 |
0 |
4 |
|
0 |
v2 |
2 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
0 |
4 |
|
|
z |
5/2 |
0 |
0 |
2 |
-1 |
1/2 |
1/2 |
0 |
0 |
-3/2 |
5 |
Теперь нельзя
выбирать разрешающими столбцы при
переменных
![]() ,
u2,
v1.
Выберем первый столбец, разрешающей –
первую строку.
,
u2,
v1.
Выберем первый столбец, разрешающей –
первую строку.
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
Сb |
Б.п |
x1 |
x2 |
|
|
u1 |
u2 |
v1 |
v2 |
y1 |
y2 |
b |
|
0 |
x1 |
1 |
0 |
0 |
4/5 |
-2/5 |
1/5 |
1/5 |
0 |
2/5 |
-1/5 |
2 |
|
0 |
|
0 |
0 |
1 |
7/5 |
-1/5 |
-2/5 |
-2/5 |
0 |
1/5 |
2/5 |
2 |
|
0 |
x2 |
0 |
1 |
0 |
-2/5 |
1/5 |
-1/10 |
2/5 |
0 |
-1/5 |
1/10 |
3 |
|
0 |
v2 |
0 |
0 |
0 |
-8/5 |
4/5 |
-2/5 |
-7/5 |
1 |
-8/5 |
2/5 |
0 |
|
|
z |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
Из симплекс-таблицы получаем опорный план
![]()
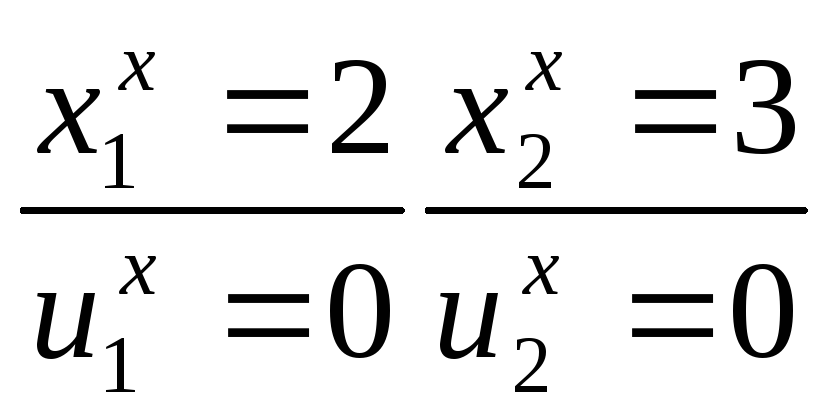
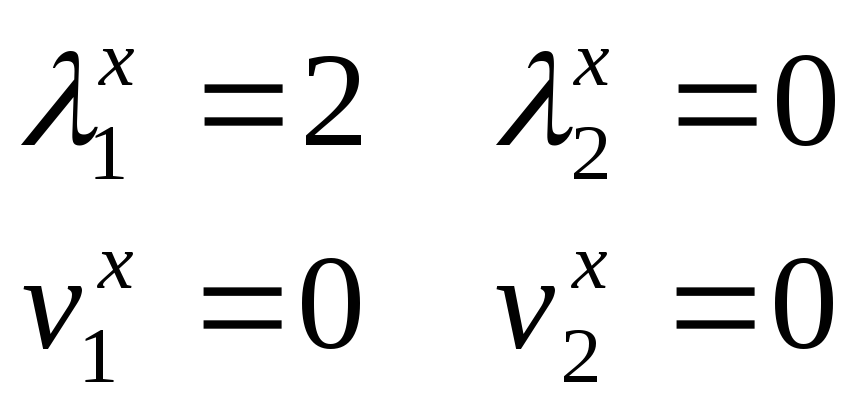
Все оценки свободных
переменных неотрицательны, значит это
оптимальное решение вспомогательной
задачи (24-26). Искусственные переменные
![]() и
и
![]() обратились в 0, тогда это опорное решение
системы уравнений (21) и оптимальное
решение задачи (17).
обратились в 0, тогда это опорное решение
системы уравнений (21) и оптимальное
решение задачи (17).
Таким образом, по
оптимальному плану требуется выпустить
2![]() первой продукции и 3
первой продукции и 3![]() второй. При этом будет получена наибольшая
прибыль fmax=29.
Ресурс 1 дефицитен, его малое увеличение
на единицу увеличивает значение критерия
на 2 единицы:
второй. При этом будет получена наибольшая
прибыль fmax=29.
Ресурс 1 дефицитен, его малое увеличение
на единицу увеличивает значение критерия
на 2 единицы:
![]()
