
- •Экономический факультет Кафедра экономической информатики в.С. Громницкий
- •Часть I. Линейное программирование 9
- •Часть II. Методы нелинейной оптимизации 81 Введение
- •Задачи принятия решений
- •Математическое моделирование
- •Часть I. Линейное программирование Глава 1. Линейные математические модели в экономических исследованиях
- •1.1. Экономические задачи
- •Задача объемного планирования
- •Задача о диете
- •1.2. Общий вид математической модели задачи линейного программирования
- •1.3. Различные формы задач линейного программирования
- •Приведение задачи линейного программирования от одной эквивалентной формы к другой
- •Примеры решения задач
- •1.4. Графическое решение задач
- •Свойства области допустимых решений
- •Глава 2. Математические свойства задачи линейного программирования
- •2.1. Свойства области допустимых решений
- •2.2. Базисные и опорные решения
- •Глава 3. Симплекс-метод решения задачи линейного программирования
- •3.1. Идея симплекс-метода
- •3.2. Векторное представление симплексных преобразований
- •3.3. Симплекс-метод в уравнениях
- •3.4. Симплекс-метод в таблицах
- •Правила построения симплекс-таблиц
- •Этапы симплекс-метода
- •3.5. Варианты разрешимости задачи линейного программирования
- •3.6. Предупреждение зацикливания симплекс-метода
- •Глава 4. Метод искусственного базиса
- •4.1. Построение начального опорного плана
- •Пример построения начального опорного плана
- •4.2. Решение задачи линейного программирования методом искусственного базиса
- •Пример решения задачи методом искусственного базиса
- •Глава 5. Теория двойственности в задачах линейного программирования
- •5.1. Построение двойственной задачи и ее экономическая интерпретация
- •Математическая формулировка двойственной задачи к произвольной задаче линейного программирования
- •Правила построения двойственной задачи
- •5.2. Математические свойства пары взаимно двойственных задач
- •Варианты разрешимости задач двойственной пары
- •Вторая теорема двойственности
- •5.3. Анализ чувствительности оптимального решения к изменению свободных членов ограничений
- •5.4. Определение оптимального решения двойственной задачи из оптимальной симплекс-таблицы прямой
- •5.5. Двойственный симплексный метод
- •Глава 6. Послеоптимизационный анализ задачи линейного программирования
- •6.1. Добавление нового ограничения
- •6.2. Добавление новой переменной
- •6.3. Изменение коэффициентов критерия
- •Изменение коэффициента критерия при свободной переменной
- •Изменение коэффициента критерия при базисной переменной
- •6.4. Изменение технологических коэффициентов
- •Изменение технологических коэффициентов при базисной переменной
- •Изменение технологических коэффициентов при свободной переменной
- •Часть II. Методы нелинейной оптимизации
- •Глава 7. Классическая теория оптимизации
- •7 (3) .1. Необходимые условия оптимальности
- •7.2. Достаточные условия оптимальности
- •Глава 8. Нелинейное программирование
- •8.1. Задачи на условный экстремум. Метод множителей Лагранжа.
- •8.2. Задачи выпуклого программирования
- •8.3. Задачи квадратичного программирования
- •Задания к лабораторным работам Лабораторная работа 1. Свойства области допустимых решений задачи линейного программирования
- •Лабораторная работа 2. Симплекс-метод. Варианты разрешимости задачи линейного программирования
- •Лабораторная работа 3. Теория двойственности в задачах линейного программирования
- •Лабораторная работа 4. Послеоптимизационный анализ задач линейного программирования
- •Перечень задач к лабораторным работам 3 и 4
- •Литература
Изменение коэффициента критерия при базисной переменной
Пусть меняется
коэффициент критерия при базисной
переменной
![]() :
:
![]()
Так как переменная
![]() – базисная переменная, то меняется
вектор коэффициентов при базисных
переменных
– базисная переменная, то меняется
вектор коэффициентов при базисных
переменных
![]() ,
в симплекс-таблице меняется крайний
левый столбец. Это повлечет изменение
большинства оценок свободных переменных.
Новые оценки вычисляются следующим
образом:
,
в симплекс-таблице меняется крайний
левый столбец. Это повлечет изменение
большинства оценок свободных переменных.
Новые оценки вычисляются следующим
образом:
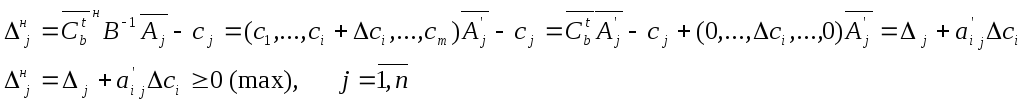
Из этой системы
неравенств находим интервал
![]() – интервал неизменности (устойчивости)
оптимального решения.
– интервал неизменности (устойчивости)
оптимального решения.
Пример:
Пусть в плане работы ЦБК по двум технологиям меняется расход древесины во время работы по второй технологии. В каких пределах можно изменять расход, чтобы прежнее решение оставалось оптимальным?
Внесем изменения в оптимальную симплекс-таблицу
![]()
|
|
|
100 |
120+ |
|
|
|
|
|
|
Св |
Бп |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
b |
|
|
x2 |
0 |
1 |
|
-1/50 |
1/60 |
0 |
100 |
|
100 |
x1 |
1 |
0 |
|
1/100 |
-1/40 |
0 |
150 |
|
0 |
x6 |
0 |
0 |
|
2/5 |
-1/6 |
1 |
1000 |
|
|
F |
0 |
0 |
|
-7/5 |
-1/2 |
0 |
27000 |

Получили, что
прежнее решение
![]() остается оптимальным, если расход
древесины по второй технологии меняется
в пределах от 50 до 150 кубометров в смену.
остается оптимальным, если расход
древесины по второй технологии меняется
в пределах от 50 до 150 кубометров в смену.
6.4. Изменение технологических коэффициентов
Рассмотрим влияние на оптимальное решение изменения матрицы технологических коэффициентов
![]()
Пусть меняется один технологический коэффициент
![]()
Так же, как в предыдущем разделе следует рассмотреть два случая
Изменение технологических коэффициентов при базисной переменной
Изменение
коэффициента
![]() при базисной переменной меняет базисную
матрицу оптимального плана. Меняется
и матрица, обратная к базисной, которая
используется в расчете основных
характеристик оптимального решения
как прямой, так и двойственной задач.
при базисной переменной меняет базисную
матрицу оптимального плана. Меняется
и матрица, обратная к базисной, которая
используется в расчете основных
характеристик оптимального решения
как прямой, так и двойственной задач.
![]()
Вычислительные затраты на пересчет матрицы, обратной к базисной, сопоставимы с затратами на повторное решение задачи симплекс-методом, поэтому не существует более эффективного способа получения оптимального решения измененной задачи.
Изменение технологических коэффициентов при свободной переменной
Пусть меняются
технологический коэффициент
![]() при свободной переменной
при свободной переменной
![]() .
.
Такое изменение технологического коэффициента не меняет базисную матрицу.
![]()
В оптимальной
симплекс-таблице изменится только один
столбец при переменной
![]() .
Его следует вычислить по формуле
.
Его следует вычислить по формуле
![]()
Посмотрим, как
изменится оценка
![]() свободной переменной
свободной переменной
![]() :
:
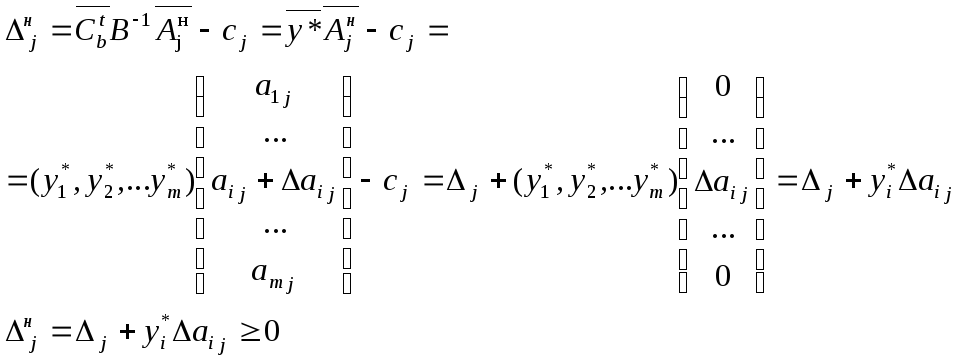
Полученное неравенство является условием сохранения прежнего оптимального решения для задачи максимизации.
Пример:
Пусть в плане работы ЦБК по трем технологиям c затратами древесины 100, 120, 110 м3 меняются объемы производства целлюлозы за смену работы по третьей технологии.
![]()
В первой
симплекс-таблице
![]() .
.
Оптимальная
симплекс-таблица до изменения
![]() :
:
|
|
|
100 |
120 |
110 |
|
|
|
|
|
Св |
Бп |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
b |
|
120 |
X2 |
0 |
1 |
8/15 |
-1/50 |
1/60 |
0 |
100 |
|
100 |
X1 |
1 |
0 |
2/5 |
1/100 |
-1/40 |
0 |
150 |
|
0 |
X6 |
0 |
0 |
8/3 |
2/5 |
-1/6 |
1 |
1000 |
|
|
F |
0 |
0 |
-6 |
-7/5 |
-1/2 |
0 |
27000 |
|
|
|
|
|
|
y1 |
y2 |
y3 |
|
В этой таблице
следует пересчитать оценку
![]() :
:

Таким образом,
если производство целлюлозы за смену
по третьей технологии будет уменьшаться
до нуля или увеличиваться до 64.286 м3,
оптимальный план останется прежним
![]() ,
третья технология не будет использоваться.
,
третья технология не будет использоваться.
Если производительность третьей технологии превысит 64.286 м3, она будет использоваться, оптимальное решение изменится. Новое оптимальное решение можно будет найти, изменив в оптимальной симплекс-таблице столбец 3 и продолжив решение симплекс-методом.
