
- •§ 2. Свойства определителей 2-го и 3-го порядка.
- •§ 3. Миноры и алгебраические дополнения элементов матрицы 3-го порядка.
- •§ 4. Разложение определителя 3-го порядка по строке или столбцу.
- •§ 5. Определители 4-го порядка.
- •§ 6. Определители n-го порядка.
- •§ 1. Виды матриц, равенство матриц.
- •§ 2. Линейные действия с матрицами и их свойства.
- •§ 3. Умножение матриц и его свойства.
- •§ 4. Обратная матрица и ее свойства.
- •§ 5. Ранг матрицы.
- •§ 1. Основные понятия.
- •§ 2. Решение систем линейных уравнений по формулам Крамера.
- •§ 3. Решение систем линейных уравнений матричным способом.
- •§ 4. Исследование систем линейных уравнений.
- •§ 5. Решение систем линейных уравнений методом Гаусса.
- •§ 6. Однородные системы линейных уравнений.
- •Тема 1. О п р е д е л и т е л и
- •Тема 2. М а т р и ц ы
- •Тема 3. С и с т е м ы л и н е й н ы х у р а в н е н и й
- •§ 2. Линейные действия с векторами и их свойства.
- •§ 3. Линейные векторные пространства. Понятие базиса.
- •§ 4. Разложение вектора по базису.
- •§ 1. Проекция вектора на ось и ее свойства.
- •§ 2. Скалярное произведение векторов и его свойства.
- •§ 3. Векторное произведение векторов и его свойства.
- •§ 4. Смешанное произведение векторов и его свойства.
- •§ 1. Основные понятия.
- •§ 2. Линейные действия с векторами в ортонормированном базисе.
- •§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
- •§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
- •§ 1. Деление отрезка в данном отношении.
- •§ 2. Вычисление расстояния между двумя точками и угла между двумя векторами.
- •§ 3. Вычисление площадей и объемов.
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
Из свойства
скалярного произведения:

 =
=
 - следует формула:
- следует формула:

Пусть
известны координаты вектора
 в О.Н.Б. {
в О.Н.Б. {
 }:
}:

 .
Тогда
.
Тогда

 = x2 + y2
+ z2 и
= x2 + y2
+ z2 и

Направляющие углы вектора - это углы, которые образует данный вектор с осями координат:
α =

 ,
β =
,
β =

 ,
γ =
,
γ =

 .
.





















Косинусы
этих углов - направляющие косинусы
данного вектора: cos α,
cos ,
cos
 .
.
x
=
 =
=
 cos
α, y
=
cos
α, y
=
 =
=
 cos
, z
=
cos
, z
=
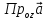 =
=
 cos
cos



Направляющие косинусы вектора являются координатами орта данного вектора:
 =
=



Пример.


 =
=
 =
=

 ,
,
 ,
,


 .
.
Из геометрического смысла скалярного произведения имеем:
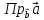 =
=
 ,
,
 =
=
 .
.
Пусть
известны координаты векторов
 и
и
 в О.Н.Б. {
в О.Н.Б. {
 }:
}:

 ,
,
 .
.
Тогда:
 =
=
 ,
,
 =
=

Пример.
 ,
,
 .
.
 =
=
 =
=
 =
=


 =
=
 =
=
 =
=

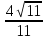
Задачи по теме 3.
. Построить
вектор

 в прямоугольной декартовой системе
координат и указать его направляющие
углы. Найти модуль и направляющие cos-ы
вектора
в прямоугольной декартовой системе
координат и указать его направляющие
углы. Найти модуль и направляющие cos-ы
вектора
 .
.
1.

 2.
2.

 3.
3.

 4.
4.


5.

 6 .
6 .

 7.
7.

 8 .
8 .


9.

 10.
10.

 11.
11.

 12.
12.

 .
Даны векторы в прямоугольной декартовой
системе координат:
.
Даны векторы в прямоугольной декартовой
системе координат:
 и
и
 .
Вычислить:
.
Вычислить:
1) скалярное произведение


2) проекции

 ,
,


3) векторное произведение

4) площадь параллелограмма, построенного
на этих векторах

1.
 ,
,
 2.
2.
 ,
,
 3.
3.
 ,
,

4.
 ,
,
 5.
5.
 ,
,
 6.
6.
 ,
,

7.
 ,
,
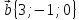 8.
8.
 ,
,
 9.
9.
 ,
,

10.
 ,
,
 11.
11.
 ,
,
 12.
12.
 ,
,

. Даны векторы в прямоугольной декартовой системе координат:
 ,
,
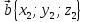 ,
,
 .
Требуется:
.
Требуется:
1) вычислить
смешанное произведение
 2) определить ориентацию этих
векторов
2) определить ориентацию этих
векторов
3) найти
объем
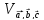 параллелепипеда, построенного на этих
векторах
параллелепипеда, построенного на этих
векторах
1.
 ,
,
 ,
,
 2.
2.
 ,
,
 ,
,

3.
 ,
,
 ,
,
 4.
4.
 ,
,
 ,
,

5.
 ,
,
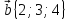 ,
,
 6.
6.
 ,
,
 ,
,

7.
 ,
,
 ,
,
 8.
8.
 ,
,
 ,
,

9.
 ,
,
 ,
,
 10.
10.
 ,
,
 ,
,

11.
 ,
,
 ,
,
 12.
12.
 ,
,
 ,
,

. Даны
векторы
 в прямоугольной декартовой системе
координат. Векторы
в прямоугольной декартовой системе
координат. Векторы
 и
и

являются линейными комбинациями этих векторов. Определить:
- при каких значениях α и β
векторы
 и
и
 будут коллинеарны (№ 1 ÷
4)
будут коллинеарны (№ 1 ÷
4)
- при каких значениях λ векторы
 и
и
 будут ортогональны (№ 5
÷ 8)
будут ортогональны (№ 5
÷ 8)
- при каких значениях λ векторы
 ,
,
 и
и
 будут компланарны (№ 9 ÷
12)
будут компланарны (№ 9 ÷
12)
1.
 = 2
= 2 + 4
+ 4 ,
,
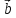 = 3
= 3 -
-
 ,
,
 ,
,

2.
 =
=
 + 2
+ 2 ,
,
 = 3
= 3 -
-
 ,
,
 ,
,

3.
 = 5
= 5 + 3
+ 3 ,
,
 = 2
= 2 -
-
 ,
,
 ,
,

4.
 = -2
= -2 +
+
 ,
,
 = 3
= 3 - 2
- 2 ,
,
 ,
,

5.
 =
=
 -
-
 ,
,
 = 4
= 4 + 2
+ 2 ,
,
 ,
,

6.
 =3
=3 - 2
- 2 ,
,
 = -2
= -2 +
+
 ,
,
 ,
,

7.
 = 2
= 2 -
-
 ,
,
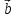 = -
= - + 3
+ 3 ,
,
 ,
,

8.
 = 2
= 2 - 3
- 3 ,
,
 = 2
= 2 +
+
 ,
,
 ,
,

9.
 ,
,
 ,
,

10.
 ,
,
 ,
,

11.
 ,
,
 ,
,

12.
 ,
,
 ,
,

Дополнительные задачи.
1.
Прямоугольная декартова система
координат OXY
на плоскости получена из прямоугольной
декартовой системы координат OXY
параллельным переносом на вектор
 .
Произвольная точка M
на плоскости имеет координаты (x,
y) в одной системе
координат и (x,
y)
- в другой системе координат. Найти связь
между этими координатами.
.
Произвольная точка M
на плоскости имеет координаты (x,
y) в одной системе
координат и (x,
y)
- в другой системе координат. Найти связь
между этими координатами.





 ,
M(x, y),
M(x,
y)
,
M(x, y),
M(x,
y)












2. Прямоугольная декартова система координат OXY на плоскости получена из прямоугольной декартовой системы координат OXY путем поворота осей на угол . Произвольная точка M на плоскости имеет координаты (x, y) в одной системе координат и (x, y) - в другой системе координат. Найти связь между этими координатами.


 ,
M(x, y),
M(x,
y)
,
M(x, y),
M(x,
y)
















3. Даны
векторы в прямоугольной декартовой
системе координат:
 ,
,
 ,
,
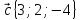 .
Найти координаты вектора
.
Найти координаты вектора
 ,
если известно, что
,
если известно, что
 = -5,
= -5,
 = -11,
= -11,
 = 20.
= 20.
4. Даны
векторы в прямоугольной декартовой
системе координат:
 ,
,
 .
Найти координаты вектора
.
Найти координаты вектора
 ,
если известно, что
,
если известно, что

 ,
,

 ,
,
 = 14.
= 14.
 4.
Геометрические
задачи.
4.
Геометрические
задачи.
