
- •§ 2. Свойства определителей 2-го и 3-го порядка.
- •§ 3. Миноры и алгебраические дополнения элементов матрицы 3-го порядка.
- •§ 4. Разложение определителя 3-го порядка по строке или столбцу.
- •§ 5. Определители 4-го порядка.
- •§ 6. Определители n-го порядка.
- •§ 1. Виды матриц, равенство матриц.
- •§ 2. Линейные действия с матрицами и их свойства.
- •§ 3. Умножение матриц и его свойства.
- •§ 4. Обратная матрица и ее свойства.
- •§ 5. Ранг матрицы.
- •§ 1. Основные понятия.
- •§ 2. Решение систем линейных уравнений по формулам Крамера.
- •§ 3. Решение систем линейных уравнений матричным способом.
- •§ 4. Исследование систем линейных уравнений.
- •§ 5. Решение систем линейных уравнений методом Гаусса.
- •§ 6. Однородные системы линейных уравнений.
- •Тема 1. О п р е д е л и т е л и
- •Тема 2. М а т р и ц ы
- •Тема 3. С и с т е м ы л и н е й н ы х у р а в н е н и й
- •§ 2. Линейные действия с векторами и их свойства.
- •§ 3. Линейные векторные пространства. Понятие базиса.
- •§ 4. Разложение вектора по базису.
- •§ 1. Проекция вектора на ось и ее свойства.
- •§ 2. Скалярное произведение векторов и его свойства.
- •§ 3. Векторное произведение векторов и его свойства.
- •§ 4. Смешанное произведение векторов и его свойства.
- •§ 1. Основные понятия.
- •§ 2. Линейные действия с векторами в ортонормированном базисе.
- •§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
- •§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
- •§ 1. Деление отрезка в данном отношении.
- •§ 2. Вычисление расстояния между двумя точками и угла между двумя векторами.
- •§ 3. Вычисление площадей и объемов.
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
§ 3. Векторное произведение векторов и его свойства.
Ориентация тройки векторов.
Упорядоченная
тройка некомпланарных векторов
 ,
,

 ,
имеющих общее начало, называется правой
тройкой, если поворот от вектора
,
имеющих общее начало, называется правой
тройкой, если поворот от вектора
 к вектору
к вектору
 виден из конца вектора
виден из конца вектора
 совершающимся против часовой
стрелки.
совершающимся против часовой
стрелки.
Упорядоченная тройка некомпланарных
векторов
 ,
,

 ,
имеющих общее начало, называется левой
тройкой, если поворот от вектора
,
имеющих общее начало, называется левой
тройкой, если поворот от вектора
 к вектору
к вектору
 виден из конца вектора
виден из конца вектора
 совершающимся по часовой стрелке.
совершающимся по часовой стрелке.


















правая тройка левая тройка
Векторным произведением векторов
 и
и
 называется вектор
называется вектор
 ,
удовлетворяющий следующим трем условиям:
,
удовлетворяющий следующим трем условиям:
1.


 ,
,



2. тройка векторов
 ,
,

 - правая тройка
- правая тройка
3.
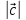 =
=

 sin
sin

Обозначение:
 =
=














Геометрический смысл векторного произведения.
Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах:
 =
=


1.
 = -
= -
 (антикоммутативность)
(антикоммутативность)
2. (λ )
) = λ(
= λ( )
(ассоциативность относительно
умножения на число)
)
(ассоциативность относительно
умножения на число)
3.

 (
( +
+
 )
=
)
=
 +
+
 (дистрибутивность)
(дистрибутивность)
4.
 =
=
 (векторный
квадрат)
(векторный
квадрат)
5.



 =
=
 (условие коллинеарности
векторов)
(условие коллинеарности
векторов)
Пример.
Найти
площадь параллелограмма,
построенного на векторах
 и
и
 ,
если
,
если
 =
=
 - 3
- 3 ,
,
 = 2
= 2 +
+
 ,
,
 = 2,
= 2,
 = 3,
= 3,

 =
=
 .
.
 =
=
 ;
;
 = (
= ( - 3
- 3 )
) (2
(2 +
+
 )
= 2
)
= 2


 - 6
- 6

 +
+


 -3
-3

 = 7
= 7

 ;
;
 = 7
= 7 = 723
= 723 = 21
= 21
 = 21.
= 21.
Пример.
Определить, при каких значениях α
и β векторы
 и
и
 будут коллинеарны:
будут коллинеарны:
 =
=
 + 2
+ 2 ,
,
 =
=
 -
-
 ,
,
 ,
,




 =
=

(
( + 2
+ 2 )
) (
( -
-
 )
=
)
=

( + 2
+ 2 )
) (
( -
-
 )
=
)
=


 -
-


 + 2
+ 2

 - 2
- 2

 =
=


 -
-
 +
+
 + 2
+ 2

 = 3
= 3

 ;
;
3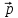

 =
=



 =
=

 rang
rang
 = 1
= 1
 =
=
 =
=
 = 0
= 0
 .
.
§ 4. Смешанное произведение векторов и его свойства.
Дана тройка векторов
 ,
,
 ,
, .
.
Смешанным произведением
 ,
,
 ,
, называется число, равное скалярному
произведению вектора
называется число, равное скалярному
произведению вектора
 на вектор
на вектор
 .
Обозначение:
.
Обозначение:
 .
.
 = (
= ( )
)
Геометрический смысл смешанного произведения.
Модуль смешанного произведения равен
объему параллелепипеда, построенного
на этих векторах:
 =
=
















1.
Смешанное произведение векторов
 ,
,
 ,
, не меняется при циклической перестановке
множителей:
не меняется при циклической перестановке
множителей:
 =
=
 =
=

2.
Смешанное произведение векторов
 ,
,
 ,
, меняет знак при перестановке двух
множителей:
меняет знак при перестановке двух
множителей:
 = -
= -
 ,
,
 = -
= -
 ,
,
 = -
= -

3. Необходимым и достаточным условием компланарности векторов является равенство нулю их смешанного произведения:
 ,
,
 ,
, - компланарны
- компланарны
 = 0
= 0
4.
 > 0
> 0
 ,
,
 ,
, - правая тройка;
- правая тройка;
 < 0
< 0
 ,
,
 ,
, - левая тройка
- левая тройка
Пример.
Найти
объем параллелепипеда, построенного
на векторах
 ,
,
 ,
, ,
если
,
если
 = 2,
= 2,
 = 3,
= 3,
 = 4, α =
= 4, α =

 =
=
 , β =
, β =

 =
=
 , γ =
, γ =

 =
=
 .
.







 - угол между векторами
- угол между векторами
 и
и









 =
=
 =
=


 = 2314
cos
= 2314
cos
 = 24
= 24
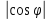 ;
;
cos
2
 + cos 2
β + cos
2
γ = 1
cos 2
+ cos 2
β + cos
2
γ = 1
cos 2
 = 1- cos 2
β - cos 2
γ = 1 -
= 1- cos 2
β - cos 2
γ = 1 -
 -
-
 =
=
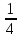
 =
=
 .
.
 = 24
= 24
 = 12.
= 12.
Задачи по теме 2.
.
Даны векторы
 .
Известны модули этих векторов и
углы между ними:
.
Известны модули этих векторов и
углы между ними:
p
=
 ,
q =
,
q =
 ,
r =
,
r =
 ,
α =
,
α =

 ,
β =
,
β =

 ,
γ =
,
γ =

 .
Вектор
.
Вектор
 является линейной
является линейной
комбинацией
векторов
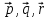 .
Найти модуль вектора
.
Найти модуль вектора
 .
.
1.
 = 2
= 2 - 3
- 3 ,
p = 1, q = 2, α =
,
p = 1, q = 2, α =
 2.
2.
 =
=
 + 2
+ 2 ,
p = 3, r = 1, β =
,
p = 3, r = 1, β =

3.
 = 2
= 2 -
-
 ,
q = 4, r = 2, γ =
,
q = 4, r = 2, γ =
 4.
4.
 =
=
 - 2
- 2 ,
p = 2, q = 1, α =
,
p = 2, q = 1, α =

5.
 =
=
 + 2
+ 2 -
-
 ,
p = 1, q = 1, r = 2, α =
,
p = 1, q = 1, r = 2, α =
 , β =
, β =
 , γ =
, γ =

6.
 = 2
= 2 -
-
 +
+
 ,
p = 1, q = 2, r = 1, α =
,
p = 1, q = 2, r = 1, α =
 , β =
, β =
 , γ =
, γ =

7.
 =
=
 + 2
+ 2 +
+
 ,
p = 3, q = 1, r = 2, α =
,
p = 3, q = 1, r = 2, α =
 , β =
, β =
 , γ =
, γ =

8.
 = 2
= 2 -
-
 -
-
 ,
p = 1, q = 2, r = 3, α =
,
p = 1, q = 2, r = 3, α =
 , β =
, β =
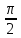 , γ =
, γ =

 .
Даны единичные векторы
.
Даны единичные векторы
 и угол между ними
α =
и угол между ними
α =

 .
Векторы
.
Векторы
 и
и

являются
линейными комбинациями векторов
 .
На векторах
.
На векторах
 и
и
 построен
построен
параллелограмм. Найти площадь S этого параллелограмма и длины его диагоналей d1 и d2.





d1
d2


1.
 =
=
 + 3
+ 3 ,
,
 = 3
= 3 -
-
 ,
α =
,
α =
 2.
2.
 = 3
= 3 +
+
 ,
,
 =
=
 -
-
 ,
α =
,
α =

3.
 =
=
 - 2
- 2 ,
,
 =
=
 +4
+4 ,
α =
,
α =
 4.
4.
 =
=
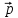 + 3
+ 3 ,
,
 =
=
 - 5
- 5 ,
α =
,
α =

5.
 = 2
= 2 -
-
 ,
,
 =
=
 + 3
+ 3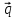 ,
α =
,
α =
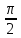 6.
6.
 = 3
= 3 +
+
 ,
,
 =
=
 - 5
- 5 ,
α =
,
α =

7.
 =
=
 - 4
- 4 ,
,
 = 3
= 3 + 2
+ 2 ,
α =
,
α =
 8.
8.
 =
=
 + 4
+ 4 ,
,
 =
=
 - 2
- 2 ,
α =
,
α =

 .
Найти объем параллелепипеда,
построенного на векторах
.
Найти объем параллелепипеда,
построенного на векторах
 ,
,
 ,
, ,
если известны модули этих векторов и
углы между ними:
,
если известны модули этих векторов и
углы между ними:
 = a,
= a,
 = b,
= b,
 = c, α
=
= c, α
=

 ,
β =
,
β =

 ,
γ =
,
γ =

 .
.
1.
a = 1,
b =
2, c
=
3,
α =
 , β =
, β =
 , γ =
, γ =
 2.
a = 2,
b =
2, c
=
3,
α =
2.
a = 2,
b =
2, c
=
3,
α =
 , β =
, β =
 , γ =
, γ =

3.
a = 1,
b =
2, c
=
4,
α =
 , β =
, β =
 , γ =
, γ =
 4.
a = 2,
b =
1, c
=
2,
α =
4.
a = 2,
b =
1, c
=
2,
α =
 , β =
, β =
 , γ =
, γ =

5.
a = 3,
b =
2, c
=
2,
α =
 , β =
, β =
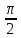 , γ =
, γ =
 6.
a = 2,
b =
3, c
=
3,
α =
6.
a = 2,
b =
3, c
=
3,
α =
 , β =
, β =
 , γ =
, γ =

7.
a = 1,
b =
2, c
=
4,
α =
 , β =
, β =
 , γ =
, γ =
 8.
a = 2,
b =
3, c
=
2,
α =
8.
a = 2,
b =
3, c
=
2,
α =
 , β =
, β =
 , γ =
, γ =

Дополнительные задачи.
1. В квадрат ABCD со стороной a вписана окружность. Точка M - произвольная точка этой окружности. Найти сумму MA2 + MB2 + MC2 + MD2.
2. Около квадрата ABCD со стороной a описана окружность. Точка M - произвольная точка этой окружности. Найти сумму MA2 + MB2 + MC2 + MD2.
3. В куб со стороной a вписана сфера. Точка M - произвольная точка этой сферы. Найти сумму квадратов расстояний от точки M до вершин куба.
4. Найти
отношение объема тетраэдра, построенного
на некомпланарных векторах
 ,
,
 ,
, ,
к объему тетраэдра, построенного на
векторах
,
к объему тетраэдра, построенного на
векторах
 +
+ ,
,
 ,
,
 .
.
 3.
Прямоугольная
декартова система координат.
3.
Прямоугольная
декартова система координат.
