
- •§ 2. Свойства определителей 2-го и 3-го порядка.
- •§ 3. Миноры и алгебраические дополнения элементов матрицы 3-го порядка.
- •§ 4. Разложение определителя 3-го порядка по строке или столбцу.
- •§ 5. Определители 4-го порядка.
- •§ 6. Определители n-го порядка.
- •§ 1. Виды матриц, равенство матриц.
- •§ 2. Линейные действия с матрицами и их свойства.
- •§ 3. Умножение матриц и его свойства.
- •§ 4. Обратная матрица и ее свойства.
- •§ 5. Ранг матрицы.
- •§ 1. Основные понятия.
- •§ 2. Решение систем линейных уравнений по формулам Крамера.
- •§ 3. Решение систем линейных уравнений матричным способом.
- •§ 4. Исследование систем линейных уравнений.
- •§ 5. Решение систем линейных уравнений методом Гаусса.
- •§ 6. Однородные системы линейных уравнений.
- •Тема 1. О п р е д е л и т е л и
- •Тема 2. М а т р и ц ы
- •Тема 3. С и с т е м ы л и н е й н ы х у р а в н е н и й
- •§ 2. Линейные действия с векторами и их свойства.
- •§ 3. Линейные векторные пространства. Понятие базиса.
- •§ 4. Разложение вектора по базису.
- •§ 1. Проекция вектора на ось и ее свойства.
- •§ 2. Скалярное произведение векторов и его свойства.
- •§ 3. Векторное произведение векторов и его свойства.
- •§ 4. Смешанное произведение векторов и его свойства.
- •§ 1. Основные понятия.
- •§ 2. Линейные действия с векторами в ортонормированном базисе.
- •§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
- •§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
- •§ 1. Деление отрезка в данном отношении.
- •§ 2. Вычисление расстояния между двумя точками и угла между двумя векторами.
- •§ 3. Вычисление площадей и объемов.
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
§ 1. Проекция вектора на ось и ее свойства.
Ось
 - это прямая, на которой:
- это прямая, на которой:
а) задан орт
 (т.е. указано направление и выбран
масштаб),
(т.е. указано направление и выбран
масштаб),
б) отмечено начало отсчета (точка О). 











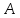
 1
1




 1
1
 1
1

 1
1
Пусть
точка A1 - проекция
точки A на ось
 ,
B1 - проекция точки
B на ось
,
B1 - проекция точки
B на ось
 (основания перпендикуляров, опущенных
соответственно из точек A
и B на ось
(основания перпендикуляров, опущенных
соответственно из точек A
и B на ось ).
).
Компонентой
вектора
 вдоль оси
вдоль оси
 называется вектор
называется вектор
 ,
где A1 - проекция
точки
,
где A1 - проекция
точки
A
на ось
 ,
B1 - проекция точки
B на ось
,
B1 - проекция точки
B на ось
 .
.
Проекцией
вектора
 на ось
на ось
 называется число, равное
называется число, равное
 ,
взятому со знаком «+», если компонента
одинаково направлена с ортом
,
взятому со знаком «+», если компонента
одинаково направлена с ортом
 и взятому со знаком «-», если компонента
противоположно направлена с ортом
и взятому со знаком «-», если компонента
противоположно направлена с ортом
 :
:
 =
=

Из
этого определения следует равенство:

Теорема. Пусть
 =
=
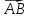 ,
,
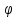 - угол между вектором
- угол между вектором
 и осью
и осью
 .
Тогда
.
Тогда


1.
 +
+
 )
=
)
=
 +
+

2.
 = λ
= λ
3.
 = 0
= 0



§ 2. Скалярное произведение векторов и его свойства.
Скалярным
произведением векторов
 и
и
 называется число, равное произведению
модулей этих векторов на косинус угла
между ними. Обозначение:
называется число, равное произведению
модулей этих векторов на косинус угла
между ними. Обозначение:

 .
.



 =
=

 cos
cos





Геометрический смысл скалярного произведения:



 =
=

 =
=


 =
=
 ,
,
 =
=






Если
 - орт
некоторой оси
- орт
некоторой оси
 ,
то
,
то
 =
=


Проекция вектора на ось равна скалярному произведению этого вектора на орт этой оси.

1.

 =
=

 (коммутативность)
(коммутативность)
2. (λ )
) = λ(
= λ(
 )
(ассоциативность
относительно умножения на число)
)
(ассоциативность
относительно умножения на число)
3.
 (
( +
+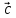 )
=
)
=

 +
+

 (дистрибутивность)
(дистрибутивность)
4.
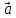
 =
=
 (скалярный квадрат)
(скалярный квадрат)
5.




 = 0 (условие ортогональности
векторов)
= 0 (условие ортогональности
векторов)
6.

 > 0
> 0
 - острый угол;
- острый угол;

 < 0
< 0
 - тупой угол
- тупой угол
Пример.
Найти модуль вектора
 ,
если известно:
,
если известно:
 = 2
= 2 -
-
 +
+
 ,
,
 = 2 ,
= 2 ,
 = 3,
= 3,
 = 4,
= 4,

 =
=
 ,
,

 =
=
 ,
,

 =
=
 .
.
 =
=

 = (2
= (2 -
-
 +
+
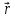 )(2
)(2 -
-
 +
+
 )
= 4
)
= 4
 - 2
- 2
 + 2
+ 2
 - 2
- 2
 +
+

 -
-

 + 2
+ 2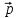
 -
-

 +
+

 =
=
=
4
 - 4
- 4
 + 4
+ 4
 -2
-2
 +
+

 +
+

 = 422
- 423
= 422
- 423 + 4240
- 234
+ 4240
- 234 + 33 +
44 =
+ 33 +
44 =
= 16 + 12 + 0 -
12 + 9 + 16 = 53 - 12
+ 9 + 16 = 53 - 12
 =
=
 .
.
Пример.
Найти длины
его диагоналей d1
и d2 параллелограмма,
построенного на векторах
 и
и
 ,
если
,
если
 =
=
 - 3
- 3 ,
,
 = 2
= 2 +
+
 ,
,
 = 2,
= 2,
 = 3,
= 3,

 =
=
 .
.





d1
d2


d1
=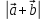 ,
d2 =
,
d2 = ;
;
 = 3
= 3 - 2
- 2 ,
,
 = -
= -
 - 4
- 4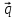 ;
;
d12
= (3 - 2
- 2 )(
)( )
= 9
)
= 9

 - 12
- 12

 + 4
+ 4

 = 922
- 12230,5
+ 433
= 36 d1
= 6.
= 922
- 12230,5
+ 433
= 36 d1
= 6.
d22
= (-
 - 4
- 4 )(-
)(-
 )
=
)
=

 + 8
+ 8

 + 16
+ 16

 = 22 + 8230,5
+ 1633
= 172 d2
=
= 22 + 8230,5
+ 1633
= 172 d2
=
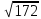 .
.
Теорема косинусов.
В произвольном треугольнике квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a2
= b2
+ c2
- 2bc
cos
 A, b2
= a2
+ c2
- 2ac
cos
A, b2
= a2
+ c2
- 2ac
cos
 B, c2
= a2
+ b2
- 2ab
cos
B, c2
= a2
+ b2
- 2ab
cos
 C.
C.
Доказательство.
 =
=
 -
-
 ,
,
 +
+
 =
=
 ,
,
 +
+
 =
=







a =
 =
= ,
b
=
,
b
=
 =
= ,
c
=
,
c
=
 =
=






a2
=
 2
=
2
=

 = (
= ( -
-
 )(
)(
 -
-
 )
=
)
=

 - 2
- 2
 +
+

 =
=
=
 2
- 2
2
- 2

 cos
cos
 A +
A +
 2
= b2
+ c2
- 2bc
cos
2
= b2
+ c2
- 2bc
cos
 A.
A.
Аналогично выводятся остальные формулы.
Следствием теоремы косинусов является
теорема Пифагора (если
 C = 90
C = 90 ,
то cos
,
то cos
 C = 0
C = 0
и c2 = a2 + b2).
Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
