§ 3. Линейные векторные пространства. Понятие базиса.

Пусть , , …, - фиксированный набор векторов.

Линейной комбинацией векторов , , …, - называется любой вектор вида

𝛌₁+ 𝛌₂ + …+ 𝛌_n, где 𝛌₁, 𝛌₂, … , 𝛌_n - некоторые действительные числа.

Множество всевозможных линейных комбинаций заданного набора векторов называется

линейным векторным пространством, натянутым на этот набор:

- линейное векторное пространство, натянутое на , , …, .

Примеры (линейных векторных пространств).

1). Дана некоторая прямая L. Пусть V₁ - множество всех векторов , лежащих на прямой L или

Параллельных этой прямой.

V₁ :

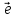
Пусть - любой ненулевой вектор множества V₁. Тогда

 V₁   = λ  

Таким образом, множество V₁ есть линейное векторное пространство, натянутое на вектор :

V₁ =

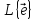
Вектор называется базисом пространства V₁.

2). Дана некоторая плоскость . Пусть V₂ - множество всех векторов , лежащих в плоскости 

или в параллельных ей плоскостях.

V₂ :

Пусть , - любые неколлинеарные векторы из множества V₂. Тогда

 V₂  = λ₁+ λ₂  

Таким образом, V₂ есть линейное векторное пространство, натянутое на векторы , :

V₂ =

Векторы , называются базисом пространства V₂.

3). Пусть V₃ - множество всех векторов в пространстве.

V₃ :

Пусть , , - любые некомпланарные векторы в пространстве. Тогда:

 V₃  = λ₁ + λ₂ + λ₃  

Таким образом, V₃ есть линейное векторное пространство, натянутое на векторы , ,:

V₃ =

Векторы , , называются базисом пространства V₃.

Ортогональный базис.

Базис, состоящий из ортогональных векторов, называется ортогональным базисом.

- ортогональный базис на плоскости:

- ортогональный базис в пространстве:

, ,

Ортонормированный базис (о.н.б.)

Ортогональный базис из единичных векторов называется ортонормированным базисом.

Обозначения: - О.Н.Б. на плоскости; - О.Н.Б. в пространстве.

- ортонормированный базис (О.Н.Б.) на плоскости:

, = = 1

- ортонормированный базис (О.Н.Б.) в пространстве:

, , , = = = 1