§ 2. Линейные действия с векторами и их свойства.
К линейным действиям с векторами относятся: сложение, вычитание векторов и умножение вектора на число.
1. Сложение векторов.
Суммой
векторов
и
называется вектор, полученный из
этих векторов по правилу треугольника
или по правилу параллелограмма.
Правило треугольника:
Начало
вектора
совпадает с концом вектора
.
Тогда суммой
+
называется вектор, начало которого
+
совпадает с
началом вектора
,
а конец - с концом вектора
.
Правило параллелограмма:
Начала
векторов
и
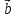совпадают. Тогда
+
суммой
+
называется вектор, идущий из их 
общего начала по диагонали параллелограмма,
построенного на этих векторах.
Свойства
нулевого и противоположного
векторов:
+
=
,
+ (-
)
=
.
Понятие суммы 2-х векторов можно обобщить на случай суммы n векторов:
…
…
+
+ … +
2. Вычитание векторов.
Разностью векторов
и
называется вектор, равный сумме
вектора
и вектора, противоположного вектору
:
=
+ (-
).
-
-
3. Умножение вектора на число.
Произведением
вектора
на действительное число λ называется
вектор
,
который определяется следующими
условиями:
= λ
При
> 1 вектор
длиннее вектора
;
при
< 1 вектор
короче вектора
.
= λ
,
λ > 0 (λ < 1)
= λ
,
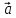λ < 0 (λ < -1)
Простейшие свойства умножения вектора на число:
0
=
1
=
(-1)
= -
(противоположный вектор)
λ
=
=
- орт вектора
,
≠
Теорема. (Необходимое и достаточное условие коллинеарности векторов)
Для того чтобы два вектора
и
были коллинеарны, необходимо и
достаточно, чтобы выполнялось равенство:
+
=
при некоторых числовых значениях
и
,
одновременно не обращающихся в ноль:
+
=
(
+
≠ 0)
Следствие. Для того чтобы два
ненулевых вектора
и
были коллинеарны, необходимо и
достаточно, чтобы выполнялось равенство:
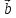= λ
при некотором действительном значении
λ:
= λ
(Число λ можно найти из равенства: λ =
,
где знак «+» выбирается в случае, если
и знак «-», если
).
Теорема. (Необходимое и достаточное условие компланарности векторов)
Для того чтобы три вектора
,
и
были компланарны, необходимо и
достаточно, чтобы выполнялось равенство:
+
+
=
при некоторых числовых значениях
,
и
,
одновременно не обращающихся в ноль:
,
,
- компланарны
+
+
=
(
+
+
≠ 0)
Следствие. Для того чтобы два
неколлинеарных вектора
и
и вектор
были компланарны, необходимо и
достаточно, чтобы выполнялось равенство:
=
+
при некоторых числовых значениях
,
:
,
,
- компланарны
=
+
ми
(
,
,
- произвольные векторы; λ, α, β -
действительные числа):
1.
+
=
+
(коммутативность
сложения векторов)
2. (
+
)
+
=
+ (
+
)
(ассоциативность сложения
векторов)
3. α(β
)
= (αβ)
(однородность
относительно умножения на число)
4. (α + β)
= α
+ β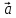
(дистрибутивность относительно
сложения чисел)
5. λ(
+
)
= λ
+ λ
(дистрибутивность
относительно сложения векторов)