7) Складні судження та їх види. Поняття про логічний сполучник.

8) Логічні відношення між складними судженнями.

Умовиводом називається така форма мислення або логічна операція, за допомогою якої із одного або декількох відомих суджень виводиться нове судження.

Умовивід складається із:

— засновків(Засновками називаються раніше відомі судження. на підставі яких робиться висновок)

(1. Будь-який мешканець нашого будинку знає англійську мову. 2. Мій приятель мешкає в нашому будинку)

— висновку(Висновком називається нове судження, отримане в результаті співставлення засновків)

(3. Отже, мій приятель знає англійську мову.)

Всю множину умовиводів за характером зв'язку між засновками та висновком поділяють на:

— дедуктивні (У дедуктивних умовиводах між засновками та висновком існує відношення логічного слідування)

— індуктивні (В індуктивних умовиводах між засновками та висновком існує відношення наведення)

У дедуктивному умовиводі ми переходимо від загального до часткового, або одиничного; в індуктивному — від одиничного до загального.

За ступенем обґрунтованості висновку умовиводи поділяють на:

— демонстративні (У демонстративних умовиводах висновок необхідно істинний)

— правдоподібні (імовірні). (, а в правдоподібних — імовірно істинний)

За кількістю засновків умовиводи поділяються на

— безпосередні (Безпосереднім умовиводом називається такий умовивід, в якому висновок отримують із одного засновку)

— опосередковані (Опосередкованим умовиводом називається такий умовивід, в якому висновок отримують із двох і більше засновків)

а) Типологія правил висновку

Правилом висновку є норма, що дозволяє із суджень однієї логічної структури як засновків отримувати судження певної логічної структури як висновок.

Умовивід аналізується на двох рівнях: синтаксичному і семантичному.

З точки зору синтаксису умовивід являє собою правило висновку.

З точки зору семантики дедуктивний умовивід являє собою відношення логічного слідування.

Правила висновку логіки висловлювань поділяються на:

— основні(правила, які змістовно очевидні і дозволяють відрізнити правильно побудовні міркування від неправильно побудованих міркувань.)

— похідні(правила, які виводяться із основних і сприяють скороченню процесу висновку)

У свою чергу основні та похідні правила поділяються на:

— прямі(правила, які вказують на безпосереднє виведення висновку із засновків.)

— непрямі(правила, які дають можливість стверджувати правомірність деяких висновків на основі визнання правомірності інших висновків)

+Основні прямі правила:

— Правило введення кон'юнкції (ВК): (А)Франція — європейська держава. (В)Іспанія — європейська держава. (А^B)Отже, Франція та Іспанія — європейські держави.

— Правило усунення кон'юнкції (УК): (А^B)Теорія та гіпотеза — форми наукового пізнання. (А)Отже, теорія — форма наукового пізнання.

— Правило введення диз'юнкції (ВД): (А)Дана форма мислення є поняттям. (АvB)Дана форма мислення є поняття або судження.

— Правила усунення диз'юнкції (УД): (АvB)Він знає мого брата або мою сестру. (~B)Він не знає мою сестру. (A)Отже, він знає мого брата.

Треба враховувати різницю смислів сполучника «або»:

1) сполучно-розділове «або»;

2) суворо розділове «або».

— Правило усунення імплікації (УІ)( «ствердження за антецедентом».): (А>В) Якщо поїзд запізнюється, то ми не встигаємо на автобус. (А)Поїзд запізнюється. (В)Отже, ми не встигаємо на автобус.

різновиди:1) (А>В), (А), (В) 2) (~А>В), (~А), (В) 3) (А>~В), (А), (~В) 4) (~А>~В), (~А), (~В)

— Правило введення еквівалендії (ВБ): (А>В)Якщо на планеті є життя, тоді там є атмосфера. (B>A)Якщо на планеті є атмосфера, тоді там є життя. (А<—>В)Отже, на планеті є життя тоді і тільки тоді, коли там є атмосфера.

— Правило усунення еквівалендії (УЕ): (А<—>В)На планеті є життя тоді і тільки тоді, коли там є атмосфера. (А>В)Отже, якщо на планеті є життя, тоді там є атмосфера.

— Правило введення подвійного заперечення (ВПЗ): (А)Ця книжка є підручником з логіки. (~ ~А)Отже, невірно, що ця книжка не підручник з логіки.

— Правило усунення подвійного заперечення (УПЗ): (~ ~А)Невірно, що курсова робота не виконана самостійно. (А)Отже, курсова робота виконана самостійно.

+Основні непрямі правила:

— Правило введення імплікації (ВІ): «Якщо із засновків П(множина засновків) і з припущення А випливає В, то можна стверджувати вивідність із цих засновків А > В».

— Правило введення заперечення (ВЗ): «Якщо із засновків і довільного припущення А випливають два суперечливих висловлювання В і ~В , то таке припущення повинно бути визнаним як хибне, істинним визнається ~А».

+Похідні правила висновку:

— Правило транзитивності імплікації (ТІ) : (А>В)Якщо мовний відрізок розповідне речення, то він є висловлюванням. (B>C)Якщо мовний відрізок є висловлюванням, то він є осмисленим. (А>C)Отже, якщо мовний відрізок розповідне речення, то він є осмисленим.

б) Обґрунтування правил висновку

- семантичне обґрунтування(Приклад з ТІ): (А>В), (B>C), (А>C) існує відношення логічного слідування, отже, засновки (А>В) і (В>С) не можуть бути істинними, а висновок (А>С) — хибним. Припустимо, що це не так (тобто, що А>В і В>С — істинні, а А>С — хибне). Тоді, А>С — хибне при умові А — і, С — х. А у засновках: якщо А — і, а С — х, то при будь-якому значенні В кон'юнкція засновків не буде істинною, а це суперечить нашому припущенню.

- Синтаксичне обґрунтування правила висновку передбачає побудову виведення останнього рядка із засновків. Доведення здійснюється таким способом: 1. Виписуємо засновки, що входять до правила. 2. Зліва виписуємо кроки доведення. 3. Справа напроти кожного кроку виписуємо його підставу (це може бути домовленість про введення чергового припущення, або певне правило). 1. А>В 2. В>С засновки 3. А припущення 4. В — (УІ по 1, 3) 5. С — (УІ по 2, 4) 6. А>С — (ВІ по 3, 5)

Правило заперечення диз'юнкції (ЗД): Відповідно до цього правила із заперечення диз'юнкції

слідує кон'юнкція заперечень висловлювань, що її складають. (~Аv~B)Невірно, що він студент або школяр.

(~А^~B)Отже, він і не студент, і не школяр. Доведення цього правила: 1. А>В 2. А(припущення 1) 3.АvВ(ВД по 2) 4. ~А (ВЗ по 1, 3) 5. В(припущення 2) 6. АvВ(ВД по 5) 7. ~В(ВЗ по 2, 6) 8. ~А^~В (ВК по 4,7)

Правило заперечення кон'юнкції (ЗК): «Із заперечення кон'юнкції слідує диз'юнкція заперечень висловлювань, що складають кон'юнкцію». (~А^~B)Невірно, що дане космічне тіло має ознаки планети і природного супутника. (~Аv~B)Отже, дане космічне тіло, або немає ознак планети, або не має ознак природного супутника. Доведення цього правила 1.~А^ ~В 2. ~ ~Аv ~ ~В(припущення) 3. ~ ~ А^ ~ ~ В(ЗД по 2) 4. ~ ~A(УК по 3) 5. А(УПЗ по 4) 6. ~ ~ В(УК по 3) 7. В(УПЗ по 6) 8. А^В(ВК по 5, 7) 9. ~АvВ(ВЗ по 1, 8)

Правило «Modus tollens» , або «від заперечення консеквентну до заперечення антецеденту» (МТ):

(А>В)Якщо він знає англійську мову, то він перекладе цей текст. (~B)Він не переклав цей текст. (~A)Отже, він не знає англійської мови. Доведення правила МТ: 1. А> 2. ~В З.А(припущення) 4. В (МТ по 1, 3) 5. ~А (ВЗ по 2, 4)

Правило простої контрапозиції (ПК): (А>В)Якщо лист написаний мною, то його зміст повинен бути мені відомим. (~B>~A)Отже, якщо мені невідомий зміст листа, то він написаний не мною. 1. А>В 2. ~В — (припущення) 3. ~А - (МТ по 1, 3) 4. ~В^~А — (ВІ по2,3)

Правило складної контрапозиції (ПСК): (А^В)>С Якщо іспит з історії є першимі і він профілюючий, то, він є вирішальним для абітурієнта-медаліста. (А^~С)> ~В Отже, якщо іспит з історії є першим, але він не вирішальний для абітурієнта-медаліста, то він не профілюючий. 1. (А^В)>С 2. А^~С (припущення) З.А(УК по 2) 4. ~С(УК по 2) 5. А^В(МТ по 1, 4) 6. АvВ(ЗК по 5)7. В(УД по 3, 6) 8. (А^~С)> ~В(ВІ по2,7)

Правило імпортації (ПІмп): A>(В>С)Якщо він добре знає англійську мову, то у випадку, якщо приїде англійська делегація він зможе виконати роль перекладача. (A^В)>С Отже, якщо він добре знає англійську мову і приїде англійська делегація, то він зможе виконати роль перекладача. 1. A>(В>С) 2. А^В(припущення) З.А(УК по 2) 4. В(УК по 2) 5. В>С(МП по 1, 3) 6. С(МП по 4, 5) 7. (A^В)>С (ВІ по 2, 6)

Правило експортації (ПЕкс): (A^В)>С Якщо дана стаття ґрунтовна за змістом і відповідає тематиці збірника, то її слід публікувати. A>(В>С)Отже, якщо дана стаття грунтовна за змістом, то у випадку, що вона відповідає тематиці збірника її слід публікувати. 1. (A^В)>С 2. А(припущення 1) 3. В(припущення 2)

4.А^В(ВК по 2,3)5. С(МП по 1, 4) 6. (В>С)(ВІ по 3, 5)7. A>(В>С) (ВІ по 2, 6)

в) Метод аналітичних таблиць

Основу методу аналітичних таблиць складає звичайне визначення таблиць істинності для пропозиційних зв'язок, а сама аналітична таблиця будується навпаки.

Таблиці називаються аналітичними тому, що розкладаючи вихідне висловлювання на елементарні висловлювання (на атоми), ми намагаємося знайти набір значень атомів, при яких би вихідне висловлювання було хибне.

Визначимо аналітичні правила для логічних зв'язок. Т позначає логічне значення «істина», а симлол F логічне значення «хиба».

Т^ - кон'юнкція А^В — істинна тоді і тільки тоді, коли А і В — істинні. ТА^В — «істинна» = ТА і ТВ,

ТА^В, ТА, ТВ.

F^ - кон'юнкція А^В хибна тоді і тільки тоді, коли або А — хибне, або В — хибне. F А^В — «хибна» = FА або FВ, FA^B, FА |(Альтернатива(або)) FВ.

Tv - Диз'юнкція А V В істинна тоді і тільки тоді, коли або А — істинне, або В — істинне.

Fv - Диз'юнкція А V В хибна тоді і тільки тоді, коли А — хибне, і В — хибне.

T> - Імплікація А > В істинна тоді і тільки тоді, коли або А — хибне, або В — істинне.

F> - Імплікація А > В хибна тоді і тільки тоді, коли А — істинне, а В — хибне.

T<-> -Еквіваленція А <-> В істинна тоді і тільки тоді, коли А — істинне, і В — істинне, або А — хибне і В — хибне.

F<-> - Еквіваленція А <-> В хибна тоді і тільки тоді, коли А — істинне, а В — хибне, або А — хибне, а В — істинне.

Т~ - Заперечення ~А істинне тоді, коли хибне А.

Р~ - Заперечення ~А хибне тоді, коли істинне А.

Т^, Fv, F>, Т~, F~ - це правила без розгалуження, а правила F^, Tv, Т>, Т<->, F<-> — це правила з розгалуженням.

Для побудови аналітичної таблиці необхідно виконати такі умови: 1. Нумерацію рядків таблиці розпочинають з 0 (нуля). 2. Наслідки відділяються від припущення горизонтальною рискою. 3. Наслідки, які отримані із одного з попередніх висловлювань позначають римськими цифрами. 4. Аналітична таблиця складається з гілок. Таблиця вважається замкненою, якщо в ній зустрічається пара висловлювань ТА і FА, а вся аналітична таблиця вважається замкненою, коли кожна її гілка замкнена.

(А^В)> (АvВ). Припустимо, що воно хибне. 0. F(А^В)>(Аv~В). І. 1. TA^B, 2. FAv~B F>,II.3.TA 4.TB T^ III.5.FA 6. F~B Fv IV. 7 TB(+) F~

Спочатку ми застосували правило F> до рядка 0 і отримали перший крок :— І із рядками 1,2; потім до рядка 1 застосували правило Т^, і отримали II крок із рядками 3, 4, а до рядка 2 застосували правило Fv і отримали III крок із рядками 5,6 і, нарешті, до рядка 6 III кроку застосували правило F~ і отримали IV крок з рядком 7. Якщо розглянути отриману гілку, то можна побачити, що вона замкнена, оскільки містить у собі ТА і FА (3 і 5 рядки), замкненою є і вся аналітична таблиця, тому, що в ній також всі гілки замкнені (в даному випадку одна). Замкненість аналітичної таблиці позначається знаком (+) (у нашому прикладі після 7 рядка). Отже, наведене висловлювання тотожно істинне, припущення про його хибність відпадає і можна стверджувати, що дане складне висловлювання коректне відносно правил висновку логіки висловлювань.

г) Умовиводи логіки висловлювань в традиційній логіці

Умовно — категоричним називається умовивід, у якому один засновок умовне судження, а другий засновок і висновок категоричні судження.

+Modus ponens(«від ствердження підстави до ствердження наслідку».) Якщо гіпотеза підтверджується на практиці, то вона стає теорією. Дана гіпотеза підтверджується практикою.Отже, вона перетворюється в теорію.

[(p>q)^p] |=q

+modus tollens(«від заперечення наслідку до заперечення підстави». Якщо у діях підозрюваного є ознаки складу злочину, то порушується кримінальна справа. Кримінальна справа стосовно громадянина N не пору-

шена. Отже, в діях громадянина N немає ознак складу злочину. [(p>q)^~q] |=~p

Чисто умовним називається умовивід у якому засновки і висновок є умовними судженнями. Якщо студент здібний, то він має досягнення у науковій роботі. Якщо студент має досягнення у науковій роботі, то його можна рекомендувати до вступу в аспірантуру. Отже, якщо студент здібний, то його можна рекомендувати до вступу в аспірантуру.[(p>q)^(q>r)] |= (p>r). «транзитивна імплікація»

Розділово — категоричним умовиводом називається умовивід у якому один засновок розділове судження, а другий засновок і висновок категоричні судження.

+Modus tollendo ponens«заперечувально-стверджуючий модус». Злочин міг скоїти N або М. N не був причетним до злочину. Отже, злочин скоїв М. [(pvq)^~p] |=q

+Modus ponendo tollens«стверджу вально-заперечу вальний модус» Цей студент киянин або іногородній. Цей студент — іногородній. Отже, цей студент не є мешканцем м. Києва. [(pVq)^q] |= ~p

При побудові розділово-категоричних умовиводів необхідно дотримуватися таких правил:

1. У стверджувально-заперечувально му модусі більший засновок має сполучник «або», який вживається у строго розділовому смислі.

2. У більшому засновку повинні бути перераховані усі альтернативи. Якщо цього не зробити, то отримаємо хибний засновок, а це означає, що такий умовивід буде не ефективним.

Студенти бувають вечірньої або заочної форми навчання. Він не є студентом заочної форми навчання. Отже, він студент вечірньої форми навчання.

Умовно — розділовим умовиводом називається умовивід, у якому один із засновків є розділовим судженням, а решта умовними судженнями.

Якщо ранкові газети повідомлять про результати референдуму, то я ще сьогодні зможу підготуватися до виступу. Якщо вечірні газети повідомлять про результати референдуму, то я лише завтра зможу підготуватися до виступу. Результати референдуму повідомлять або ранкові, або вечірні газети. Отже, я зможу підготуватися до виступу або сьогодні, або завтра.

В залежності від кількості альтернатив у розділовому засновку лематичні(умовно-розділові) умовиводи поділяють на:

а) дилеми (дві альтернативи);

б) трилеми (три альтернативи);

в) полілеми (чотири і більше альтернатив).

За якістю наслідку (заперечувальний або стверджувальний) дилеми поділяють на:

— конструктивні(дилема у висновок якої входять наслідки умовних засновків.)

— деструктивні(дилема, висновок якої складається із заперечення підстав умовних засновків.)

За складністю наслідку дилеми поділяють на:

— прості(висновком якої є наслідок умовного засновку, або заперечення підстави умовного засновку.)

— складні(висновком якої є диз'юнкція наслідків умовних засновків або заперечення підстав умовних засновків)

Якщо студент здібний, то він успішно складе сесію. Якщо студент старанний, то він успішно складе сесію. Студент або здібний, або старанний. Отже, студент успішно складе сесію.[(p>q)^(r>q)^(pvr)]|=q(проста конструктивна дилема(ПКД) (Непряме похідне правило висновку)

Якщо N вчинив протиправні дії, то N понесе матеріальні збитки. Якщо N вчинив протиправні дії, то N понесе моральні збитки. N не понесе ні матеріальних , ні моральних збитків.Отже, він не вчиняв протиправних дій.[(p>q)^(p>r)^(~qv~r)] |= ~p (проста деструктивна дилема(ПДД) (Непряме похідне правило)

Якщо іспит вступний, то він може впливати на конкурс. Якщо іспит семестровий, то він може впливати на отримання стипендії. Іспити бувають вступні або семестрові. Отже, іспити можуть впливати або на конкурс, або на отримання стипендії. [(p>q)^(r>q)^(~qv~s)] |= (~pv~r)(складна конструктивна дилема (СКД)(пряме)

СДД - Непряме похідне правило

Висновки із категоричних висловлювань поділяються на:

• безпосередні(дедуктивний умовивід, у якому висновок отримують із)

а) обернення, перетворення, протиставлення предикату;

б) умовиводи за логічним квадратом.

— опосередковані(відносять простий категоричний силогізм.)

Обернення. метою безпосереднього умовиводу шляхом обернення є отримання інформації про відношення Р до S у структурі категоричного судження. S e P | P e S. оберненням називається такий безпосередній умовивід у висновку якого суб'єктом стає предикат засновку, а предикатом — суб'єкт засновку .

Якщо у ролі засновку маємо судження А, то у висновку отримуємо судження І: Всі підручники мають методичний зміст. Отже, деякі книги методичного характеру є підручниками.

Якщо у ролі засновку наявне судження Е, то у висновку також отримуємо судження Е: Жодний мій знайомий не був учасником минулого кінофестивалю. Отже, жоден учасник минулого кінофестивалю не був серед моїх знайомих.

У випадку із судженням І висновком матимемо судження І: Деякі книги нашої бібліотеки є рідкісними. Отже, деякі рідкісні книги є в нашій бібліотеці.

Cудження О оберненню не підлягає. «Деякі рослини не є деревами».

Обернення суджень Е і І називають оберненням без обмежень. Обернення судження А називають оберненням з обмеженням.

Перетворення. S e P | S ne e ne P. В умовиводі шляхом перетворення ми отримуємо висновок де суб'єктом є суб'єкт засновку, а предикатом є поняття, що суперечить предикату засновку. Це стає можливим завдяки зміні якості засновку. Судження А перетворюється у судження Е.( Усі мої друзі мають вищу освіту. Отже, серед моїх друзів немає жодного, хто не мав би вищої освіти.) Судження Е перетворюється у судження А.( Жоден мій приятель не має вищої освіти. Отже, усі мої приятелі є людьми без вищої освіти.). Судження І перетворюється у судження О(Деякі мої приятелі вивчають англійську мову. Отже, деякі мої приятелі не належать до людей, що не вивчають англійську мову.). Судження О перетворюється в судження І(Деякі науки не є гуманітарними. Отже, деякі науки є не гуманітарними.)

Протиставлення предикату. S e P | ne-P e S. Протиставленням предикату називається такий безпосередній умовивід у результаті якого отримують висновок суб'єктом якого є поняття, що суперечить предикату засновку, а предикатом стає суб'єкт засновку. Із судження А шляхом протиставлення предикату отримують судження Е(Будь-яка теорія підтверджується на практиці.Отже, все, що не підтверджується на практиці не теорією.). Із судження Е шляхом протиставлення предикату отримують судження А.(Жоден мій приятель не має вищої освіти.Отже, деякі люди без вищої освіти мої приятелі.). Із судження О шляхом протиставлення предикату отримують судження І.(Деякі студенти не є учасниками конференції. Отже, деякі не учасники конференції студенти.). Із судження І шляхом протиславлення предикату висновок отримати неможливо.

Умовиводи за «логічним квадратом». відношень існує чотири види: підпорядкування, суперечності, противності і підпротивності. Умовиводи, які будуються із урахуванням цих 4-х типів відношень між категоричними судженнями, називають умовиводами за «логічним квадратом».

Побудова умовиводів за «логічним квадратом» підпорядкована певним правилам, які: по-перше, забезпечують правильність умовиводу в кожному конкретному випадку; а по-друге, дають систематичний огляд всіх можливих міркувань такого типу.

Правила висновку умовиводів за «логічним квадратом» поділяються на:

— основні

• похідні.

б) Простий категоричний силогізм(дедуктивний умовивід, який складається із двох засновків і висновку, представлених судженнями виду: АSР,ЕSР, ІSР, OSР.)

Будь-який умовивід (М) породжує нове знання (Р). 2. Оскільки категоричний силогізм (S) належить до

класу умовиводів (М), то Отже, він (S) породжує нове знання (Р). за структурою складається із трьох термінів: S, М, Р.

Термін, що входить до висновку як його суб'єкт називається меншим і позначається буквою S.Термін, який виконує роль предиката висновку називається більшим і позначається буквою Р.Термін, що входить в обидва засновки, але відсутній у висновку, називається середнімі позначається буквою М.

Якщо розглядати структуру силогізму в залежності від розташування трьох термінів, то можливі чотири

схеми: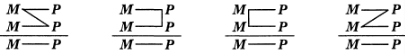

Ці схеми називають фігурами категоричного силогізму, тобто різновидами категоричного силогізму, які визначаються розташуванням середнього терміна.

Різновиди категоричного силогізму розрізняють за формами засновків і висновку. їх прийнято називати модусами категоричного силогізму.

При побудові категоричного силогізму дотримуються певних правил, які поділяються на:

а) загальні правила категоричного силогізму(ЗПС) 1. У простому категоричному силогізмі повинно бути лише три терміни. 2. Середній термін повинен бути розподіленим хоча б в одному з засновків. 3. Якщо крайній термін розподілений (або не розподілений) у засновку, то він повинен бути розподіленим (або не розподіленим) у висновку. 4. Якщо один із засновків заперечувальне судження, то і висновок буде заперечувальним судженням. 5. Якщо один із засновків часткове судження, то і висновок буде частковим судженням. 6. Із двох заперечувальних суджень висновок отримати не можливо. 7. Із двох часткових суджень висновок отримати неможливо.

б) спеціальні правила фігур. Перша фігура: 1. Більший засновок — судження загальне. 2. Менший засновок — судження стверджувальне. Друга фігура: 1. Більший засновок повинен бути загальним судженням. 2. Один із засновків заперечувальне судження. Третя фігура: 1. Менший засновок — стверджувальне судження. 2. Висновок — часткове судження. Четверта фігура: 1. Якщо більший засновок стверджувальне судження, то менший повинен бути загальним судженням. 2. Якщо один із засновків заперечувальне судження, то більший засновок повинен бути загальним судженням.

Використовуючи ЗПС і спеціальні правила фігур, для кожної фігури можна вивести усі правильні модуси. У межах кожної фігури можливі 16 комбінацій засновків від чотрирьох видів суджень АSР, ЕSР, ІSР, OSР: АА ЕА ІА ОА

АЕ ЕЕ ІЕ OЕ

АІ ЕІ II OI

АО ЕО IO OO

Перше правило виключає повністю комбінації 3 і 4 колонок. Варіанти 2 і 4 першої колонки суперечать першому правилу фігури. Варіанти 2 і 4 другої колонки виключаються з розгляду за 6 — ЗПС.

Отже, залишаються комбінації АА, АІ, ЕА, ЕІ із яких отримують модуси ААА, АII, ЕАЕ, ЕІО. Кожний модус має конкретне ім'я, що використовується як певний мнемонічний засіб: Barbara, Celarent, Darii, Ferio .

Логічна коректність модусів II, IIІ та IV фігур встановлюється за допомогою модусів першої фігури та відповідних правил висновку.

Для того, щоб встановити правильність силогізму необхідно здійснити такі кроки:

а) Знайти засновки і висновок даного силогізму.б) Визначити середній (М), більший (Р) та менший (S) терміни досліджуваного силогізму. в) Визначити більший та менший засновок. г) Перевірити дотримання загальних правил силогізму. д) Втановити фігуру досліджуваного силогізму. є) Перевірити чи відповідає даний силогізм правилам, тієі фігури за якою він побудований.

Силогізм, у якому пропущено один із засновків, або висновок називається скороченим силогізмом, або ентитемою.

Термін «ентимема» походить від грецького inthymos, що означає «в думці», «на думці» тощо.

Існує три види ентимеми: а) Ентимема з пропущеним більшим засновком.«Земля має природний супутник, тому що вона планета»; б) Ентимема з пропущеним меншим засновком.«Земля має природний супутник, тому що усі планети мають природні супутники»; в) Ентимема з пропущеним висновком.«Всі планети мають природний супутник, а Земля — планета».

Для того щоб відновити силогізм у повному вигляді необхідно здійснити такі кроки: а) Визначити, що дано в ентимемі: два засновки, або один засновок і висновок; б) Знайти терміни силогізму в наявних частинах силогізму; в) Відновити по знайдених термінах силогізму відсутню частину силогізму; г) Застосувати алгоритм перевірки силогізму до реконструйованого силогізму.

Недедуктивні умовиводи(індуктивні умовиводи, умовиводи за аналогією)

— індуктивні умовиводи(умовивід, в якому із одиничних або часткових суджень виводиться загальне судження)( Земля має природний супутник. Марс має природний супутник. Юпітер має природний супутник.

Земля, Марс, Юпітер ... це планети Сонячної системи. Отже, ймовірно, що будь-яка планета Сонячної системи має природний супутник.)

Індуктивні умовиводи поділяються на:

— повну індукцію(такий умовивід, у якому на підставі притаманності ознаки кожному предметові деякої множини робиться висновок про належність цієї ознаки всім предметам цієї множини.)(N знав потерпілого. М знав потерпілого. К знав потерпілого. Z знав потерпілого. N, М, К, Z — це всі мої найближчі родичі. Отже, всі мої найближчі родичі знали потерпілого.)

— неповну індукцію(висновок про весь клас предметів базується на вивченні тільки деяких предметів, що належать до даного класу.)(Київський університет імені Тараса Шевченка має статус національного вузу. Харківська юридична академія імені Ярослава Мудрого має статус національного вузу. Український аграрний університет має статус національного вузу.Київський університет імені Тараса Шевченка, Харківська юридична академія імені Ярослава Мудрого, Український аграрний університет — це основні вузи України. Отже, ймовірно, що всі основні вузи України мають статус національного вузу.)

У свою чергу неповна індукція має два види:

— популярна індукція(у якому відсутній конкретний метод відбору засновків. Популярна індукція відрізняється від повної тим, що вона використовується при аналізі кінцевих неосяжних і нескінченних множин предметів. її ще називають «індукція через простий перелік при відсутності контрприкладу».)( Франція — республіка. Австрія — республіка. Італія — республіка. Франція, Австрія, Італія — європейські держави. Отже, всі європейські держави мають республіканську форму правління.)

Для того, щоб підвищити надійність висновку у популярній індукції необхідно дотримуватися таких вимог: а) збільшувати число досліджуваних випадків; б) збільшувати різноманітність досліджуваних випадків;

в) враховувати характер зв'язку між досліджуваними предметами та їх ознаками.

— наукова індукція або метод знаходження причинних зв'язків.

Всього таких методів п'ять:

1) Метод єдиної подібності; «Якщо яка-небудь умова К постійно передує появі явища х при зміні всіх інших умов, то ймовірно ця умова є причиною х».(Повторення осіб---> Явище)

2) Метод єдиної відмінності; «Якщо за наявності умови К настає досліджуване явище х, а за її відсутності явище не настає, то К є причиною появи явища х».( «У повітрі, де є кисень, свічка горить.У повітрі, де відсутній кисень, свічка гасне. Отже, наявність кисню є причиною горіння свічки».)

3) З'єднаний метод подібності і відмінності; «Якщо два або більше випадків, коли настає явище х подібні тільки за однієї умови К, у той час як два або більше випадків, коли дане явище х відсутнє, відрізняються від перших випадків тільки тим, що відсутня умова К, то К є причиною х».(Крадіжка, коли є А і немає крадіжки, коли немає А)

4) Метод супутних змін; «Якщо із зміною умови К у тій же мірі змінюється деяке явище х, а решта явищ залишаються незмінними, то ймовірно, що К є причиною х». «За всіх однакових умовах збільшення сили струму в колі супроводжується збільшенням нагрівання провідника».

5) Метод залишків. «Якщо складні умови породжують складну дію і відомо, що частина умов викликає частину цієї дії, то залишкова частина умов викликає залишкову частину дії». АВ є причиною складного явища а, в. В є причиною в. Отже, А є причиною а.

— умовиводи за аналогією(у якому судження про притаманність певної ознаки деякому об'єктові виводиться на основі подібності цього об'єкту з іншим об'єктом.)(«Аналогією називається такий умовивід, де від подібності двох предметів у деяких ознаках робиться висновок про схожість цих предметів у інших ознаках».)

Зразком аналогії називається об'єкт ознака яко- го переноситься на другий об'єкт.

Суб'єктом аналогії називається об'єкт на який переноситься ознака.

Зразок і суб'єкт називаються термінами аналоги. Ознака, яка переноситься із зразка на суб'єкт називається переносною ознакою. Ознака, яка одночасно притаманна зразку і суб'єкту і яка є підставою для переносу ознаки, що нас цікавить називається основою аналогії.

До структури аналоги входять чотири види суджень:

1) судження про наявність основи у зразка; (Засновок)

2) судження про наявність основи у суб'єкта; (Засновок)

3) судження про наявність переносної ознаки у зразка; (Засновок)

4) судження про наявність переносної ознаки у суб'єкта.(Висновок)

Існує два види аналогій:

— Аналогією властивостей називається такий умовивід, в якому переносною ознакою є властивість. (гіпотези про існування життя на Марсі.) Якщо позначити Землю і Марс відповідно термами а і в, Q ознаку

«мати життя» через предикатор Q, то обргунтовуване твердження «На Марсі є життя» матиме вигляд — Q(b). Порівнюючи властивості, які має Марс і Земля виявляють, що Марс і Земля є планетами Р1, вони обертаються навколо Сонця Р2, світять відображеним світлом Р3 тощо. Отже, має місце їх схожість за ознаками РІ, Р2, Р3 . Це й дає підставу зробити висновок за аналогією властивостей, що «На Марсі є життя».

«В одному районі міста зафіксовано 3 випадки крадіжок антикварних речей, шляхом проникнення в квартиру через вхідні двері за допомогою портативного електрозварювального апарату. У результаті розслідування виникла версія, що це були одні й ті самі злочинці». Підставою для аналогії були ознаки:

1) характер злочину (крадіжка); 2) однотипність краденого (антикваріат); 3) шлях і спосіб проникнення.

—Аналогією відношення називається умовивід в якому переносною ознакою є ознака відношення.) (Прикладом аналогії відношень є відкриття Резерфордом планетарної моделі атому.) Якщо ми маємо дві системи упорядкованих об'єктів: а = (а1, а2 , ... , аn ) і в = (вІ, в2 , ... , вп ), між якими існують однакові відношення, то міркування можна побудувати так:

Для підвищення міри ймовірності аналогії треба дотримуватися таких вимог: 1. Число спільних для зразка і суб'єкта ознак повинно бути якомога більшим. 2. Основа аналогії повинна бути суттєвою для зразка і суб'єкта аналогії. 3. Спільні ознаки для зразка і суб'єкта повинні бути найрізноманітніші. 4. Переносна ознака повинна бути зв'язана із спільними ознаками.

АРГУМЕНТАЦІЯ

Аргументацію можна визначити як спосіб міркування, який складається із доведення і спростування, в ході яких формується переконання в істинності чи хибності якогось положення як у самого автора так і у опонентів

Термін «доведення» має декілька значень. По-перше, «доведенням» називають факти, за допомогою яких встановлюється істинність певного положення. По-друге, «доведенням», позначають джерела доказів, наприклад, літописи, архіви, оповіді очевидців, мемуари тощо. по-третє, «доведенням» називають логічну процедуру, в ході якої встановлюється істинність певного положення за допомогою положень, істинність яких

уже встановлена раніше.

Структура доведення складається із:

— Теза — це думка або положення, істинність якої потрібно довести.(«Земля має еліптичну орбіту руху», «Хто організатор вбивства президента Дж. Кеннеді?»;)

У судовій практиці розрізняють:

+ основну тезу(положення, із якого виливають (або йому підпорядковуються) декілька явно сформульованих положень.)

+підлеглу або часткову тезу(положення, яке стає тезою лише тому,що завдяки йому доводиться основна теза)

— аргументів це думка, істинність якої уже встановлена раніше, і яка може бути використана для обґрунтування істинності довільного положення.

До аргументів відносять:

1) факти дійсності(зроблене, здійснене); (По-перше, під фактом розуміють істину, подію або результат; по-друге, факт визначають як дещо реальне на протилежність вигаданому; по-третє, під фактом розуміють конкретне, одиничне на відміну від абстрактного, загального; по-четверте, факт трактують як особливого роду, положення, що фіксує емпіричне знання, яке протиставляється теорії або гіпотезі. У межах нашого дослідження під фактом розуміється явище або подія, що мають місце в дійсності, і які правильно відображені в судженні.)( подію затемнення Сонця можна пояснити як явище, що відповідає законам астрономії і як знак різних соціальних катаклізмів (війна, голод, зміни влади тощо.).)

2) закони(це положення, які відображають суттєві необхідні та загальні зв'язки і відношення.)( щоб встановити причетність підозрюваного до злочину ми повинні зібрати докази по цій справі. Але самі докази поза правовою нормою не дають можливість зробити відповідні висновки. Лише тоді, коли факти співставляються з юридичною нормою вони можуть стати аргументами. Іншими словами, у ході слідства і судового процесу, висновки логічно спираються на факти дійсності і на відповідні статті закону.)

Серед законів розрізняють:

— закони природи (закони астрономії, фізики, математики, хімії і ін.);

— закони суспільства (закони соціології, економіки, права, моралі і ін.).

3) аксіоми(це положення які не потребують доведення) У гуманітарних науках деякі залежності теж можуть виконувати функцію аргументів. Маються на увазі такі: — категоричний імператив І. Канта: «Дій так, щоб

ти завжди ставився до людства як у своїй особі, так і в особі будь-кого іншого також, як до мети й ніколи не

ставився б до нього тільки як до засобу»; — деонтичний принцип: «Все, що не заборонено, те дозволено»; — презумпція невинності: «Будь-хто вважається невинним, доки не доведено протилежне».

4) дефініції(якщо необхідно довести, що дії обвинувачуваного є шахрайством, то вказують не тільки на факти,

що зібрані по даній справі, а й посилаються на статтю кримінального кодексу, яка описує шахрайство.)

5) раніше доведені положення. (Будь-яка наука включає в себе принципи, теорії, наукові судження, які мають логічне обґрунтування і підтверджені практикою. Саме вони й можуть виступати аргументами. Посилання на такі аргументи є достатнім для обґрунтування тези.)

—Демонстрація — це спосіб, форма зв'язку тези і аргументів. Демонстрація як процес виведення тези із аргументів завжди має форму умовиводу. Зазначимо, якщо стверджують, що демонстрація це завжди умовивід, то мають на увазі не те що доведення це якийсь новий вид умовиводу, поряд із описаним вище умовиводом як формою мислення, це — по-перше. А, по-друге, не будь-який умовивід є доведенням.

+ Демонстрація У формі дедуктивного умовиводу

+ Демонстрація У формі індуктивного умовиводу.

Види доведення:

-Прямим називається доведення, в якому теза безпосередньо випливає із аргументів. для доведення судження «Підручник з історії є джерелом інформації» застосовуємо пряме доведення. «Підручник з історії є джерелом інформації»—теза;Судження1.«Будь-яка книга є джерелом інформації» — аргумент Судження2. «Підручник з історії належить до множини книг»- аргумент

-Непрямим доведенням називається такий вид доведення у якому істинність тези випливає із хибності антитези.( Антитезою називають положення, яке суперечить тезі.)

— апагогічні В апагогічному доведенні процес обґрунтування тези ніби-то відводиться у бік від поставленої мети. Тобто замість того щоб послатися на аргументи, які прямо і позитивно підтверджують істинність тези, висувають судження, яке суперечить тезі, потім із нього виводяться наслідки, що приводять до суперечності. Це дає підставу відкинути антитезу(судження, що суперечить тезі)і визнати істинність тези. Щоб обґрунтувати довільну тезу потрібно здійснити такі кроки: — висувають антитезу, яку тимчасово вважають істинною;— із неї виводять відповідні наслідки. Якщо дані наслідки суперечать дійсності, положеннь, істинність яких визнана раніше, то цим самим встановлюється хибність антитези і визнається істинність тези.

Потрібно обґрунтувати тезу: «Підозрюваний К. причетний до крадіжки». Аргументів маємо обмаль. Тому застосовуємо апагогічне доведення.«Підозрюваний К. причетний до крадіжки» — теза «Підозрюваний К. не причетний до крадіжки» — антитеза Виводимо наслідки: «Якщо К. не причетний до крадіжки, то на місці злочину не повинно бути його слідів. У результаті проведеного розслідування було встановлено, що на місці злочину К. залишив відбитки пальців, у будинку К. знайдено знаряддя злочину, у підвалі гаража К. знайдена частина крадених речей».

— розділові: Його суть полягає в побудові розділового судження, одним із елементів якого є теза. Інші структурні елементи цього розділового судження є несумісними із тезою. За формою, або за демонстрацією цей вид доведення репрезентований розділово-категоричним умовиводом.

На відміну від прямого доведення, у якому безпосередньо виводиться істинність тези із істинності аргументів, у непрямому доведенні обґрунтовують хибність суджень, які певним чином пов'язані з тезою. Тому у непрямомі доведенні можуть виникати помилки.

«Він є або студентом старших курсів, або аспірантом, або молодшим науковим співробітником». Наступним кроком у побудові розділового доведення є встановлення хибності несумісних із тезою суджень. У ході дослідження виявлено, що особа про яку йдеться в розділовому судженні, не є ні студентом старших курсів, ні аспірантом..

Таким чином, ця людина є молодшим науковим співробітником. Він є або студентом старших курсів, або аспірантом, або науковим співробітником. Невірно, що він студент старших курсів, і невірно, що він аспірант.Отже, він є молодшим науковим співробітником.

Спростуванням називається така логічна операція, за допомогою якої встановлюють хибність або необґрунтованість тези.

1) Спростування тези; це логічна операція, завдяки якій встановлюється хибність тези.

а) спростування тези фактами; (Метал тоне у воді і один з металів не тоне)

б) спростування тези шляхом доведення істинності нової тези; (Всі, не всі, деякі)

в) спростування тези шляхом виведення із неї наслідків, що суперечать дійсності. Процедура спростування тези таким способом передбачає такі кроки: 1. Вводиться припущення, що наявна тези істинна; 2. Із прийнятої тези виводять наслідок. 3. Застосовують правило умовно-категоричного силогізму. «Якщо наслідок хибний, то основа буде хибною».(Є життя на Венері, але температура, тому немає)

2) Спростування аргументів;

-1) встановлення хибності аргументів; Якщо встановлюють хибність аргументів, які використовуються у доведенні, то цим самим теза відкидають як необґрунтовану.

-2) встановлення недостатності аргументів відносно тези; Цей спосіб спростування передбачає констатацію

недостатності аргументів для висунутої тези, тобто істинності аргументів не вистачає для визнання істинності тези. У таких випадках потрібно відшукати нові аргументи.

-3) виявлення сумніву в істинності аргументів; Суть цього виду спростування полягає у встановленні такого факту, що аргументи на які посилаються в даному доведенні самі потребують доведення їх істинності.

-4) виявлення сумніву в надійності джерела аргументів. Суть даного способу спростування полягає в

демонстрації недовіри до автора, що висловлює аргумент,або до фактичного матеріалу, на якому базується цей аргумент.

3) Спростування демонстрації. Суть цього виду спростування полягає у знаходженні помилок у формі доведення. Відомо, що формою доведення виступає завжди конкретний вид умовиводу. Тому-то виявлення порушень правил при побудові такого умовиводу, є підставою для визнання доведення неспроможним. Будь-яка планета є космічним об'єктом. Місяць космічний об'єкт. Отже, Місяць є планета.

Правила і помилки стосовно тези

Правила:

1) Теза повинна бути ясно і чітко сформульована(Під чіткістю формулювання судження розуміють явну вказівку всіх основних смислових частин судження:а) якщо теза є простим судженням, то повинні бути

виділені його логічний підмет(суб'єкт)і логічний присудок(предикат);б)якщо якийсь із суб'єктів представлений загальним поняттям, то потрібно чітко обумовити його кількісні характеристики («Всі» або «Деякі»).) маємо тезу: «Твори Л.Толстого не можна прочитати за один день». Що мається на увазі: Чи кожен

твір не можна прочитати за один день, чи деякі? Чи коли зібрати все написане великим письменником?.

в) чітко визначеними повинні бути модальні характеристики судження. г) при формулюванні тези складних суджень треба чітко визначити смисл логічних сполучників, які утворюють ці судження.( «Інформацію про результати референдуму подадуть або вранішні, або вечірні газети»,)

Не можна також доводити або спростовувати те, що пов'язане із індивідуальними уподобаннями людей.

Ілюстрацією цього є теза: «Відпочинок в Криму кращий від відпочинку в Закарпатті».