Параметрические уравнения плоскости.

Пусть в пространстве заданы два неколлинеарных вектора и и точка . Тогда в пространстве существует единственная плоскость P, проходящая через параллельно векторам и . Составим её уравнение (рис. 2.2).

O

Рис. 2.2.

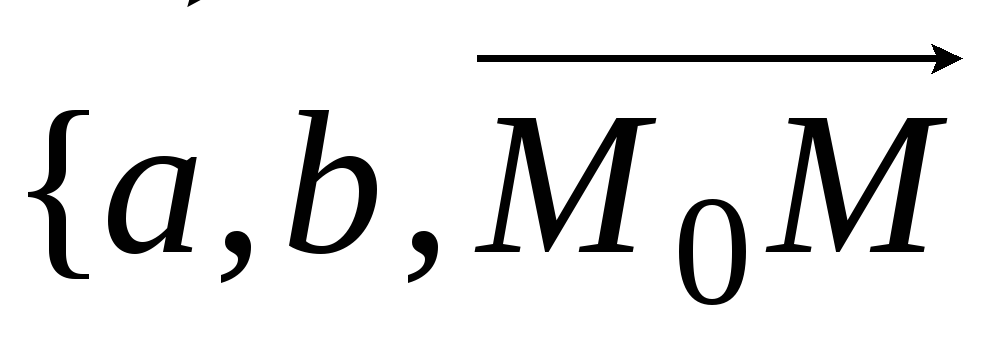– компланарны} – компланарны}.

По критерию компланарности

, (5')

или

. (5)

Уравнения (5') и (5) называются векторными параметрическими уравнениями плоскости.

Пусть теперь векторы и заданы своими координатами: , . Как обычно, обозначим , . Переписав уравнение (5) в координатах, получаем параметрические уравнения плоскости:

.

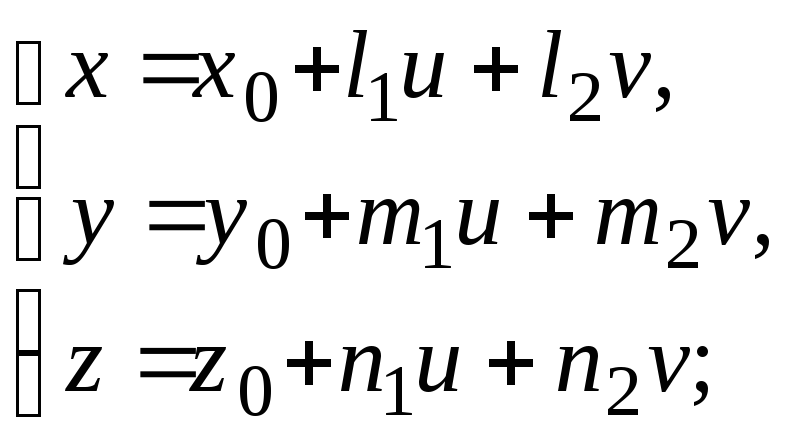
Заметим, что в параметрических уравнениях плоскости коэффициенты при параметрах и – координаты векторов, параллельных этой плоскости, а свободные члены – координаты некоторой ее точки.

Вспомним ещё один критерий компланарности: три вектора компланарны в том и только в том случае, когда их смешанное произведение равно нулю. Так как смешанное произведение в координатах вычисляется через определитель третьего порядка, получаем ещё одно уравнение плоскости:

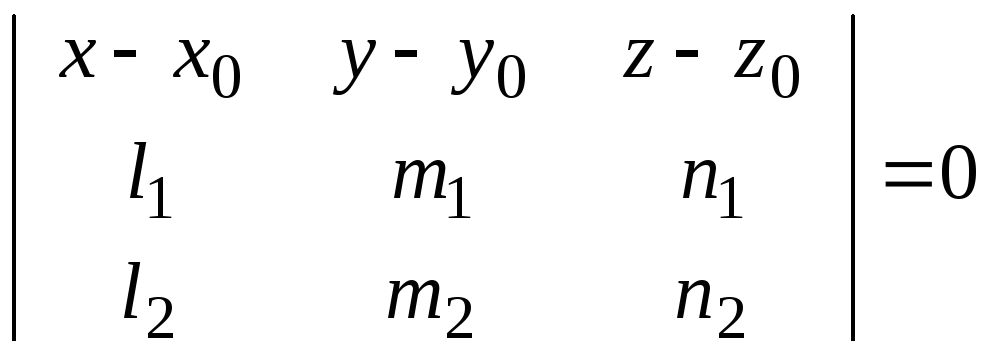. (6)

После преобразований из (6) получается общее уравнение плоскости.

Вывод: чтобы составить уравнение плоскости надо знать какую-нибудь её точку и либо нормальный вектор плоскости, либо два неколлинеарных вектора, которые этой плоскости параллельны.

§ 3. Основные виды уравнений прямой в пространстве

Н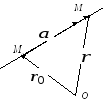аправляющим вектором прямой называют любой ненулевой вектор, параллельный этой прямой.

Если в пространстве заданы точка и вектор , то в пространстве существует единственная прямая , проходящая через точку параллельно вектору . Составим ее уравнение. Имеем (рис.2.3): .

Рис.2.3 Так как, на основании одного из критериев коллинеарности получаем:

. (1')

Раскрыв скобки в (1') и обозначив , получим уравнение:

. (1)

Уравнения (1) и (1') называются векторными уравнениями прямой в пространстве. Ещё один критерий коллинеарности (Т- 1 § 1 главы 1) приводит нас к следующим уравнениям:

, (2')

(2)

Уравнения (2) и (2') называются векторными параметрическими уравнениями прямой.

Предположим, что в заданной системе координат , , . Записав уравнение (2) в координатах, получаем параметрические уравнения прямой в пространстве:

.

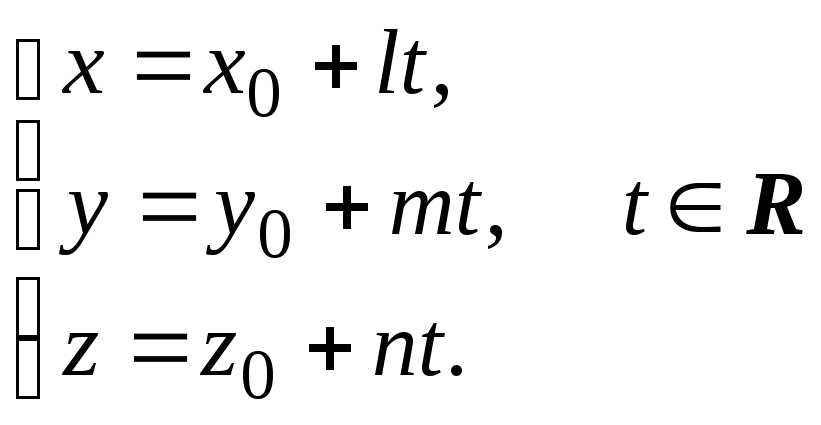В параметрических уравнениях прямой коэффициенты при – координаты направляющего вектора прямой, а свободные члены – координаты некоторой её точки.

Критерием коллинеарности векторов также является пропорциональность их координат. Этот критерий дает нам следующие уравнения:

,

которые называются каноническими уравнениями прямой в пространстве. Кроме того, прямую в пространстве можно задать в виде пересечения непараллельных плоскостей, т.е. в виде системы уравнений:

–

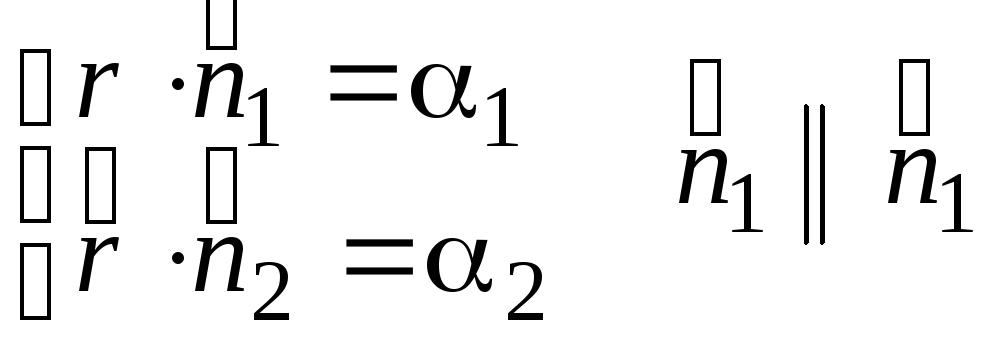
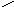векторная форма записи, или

,

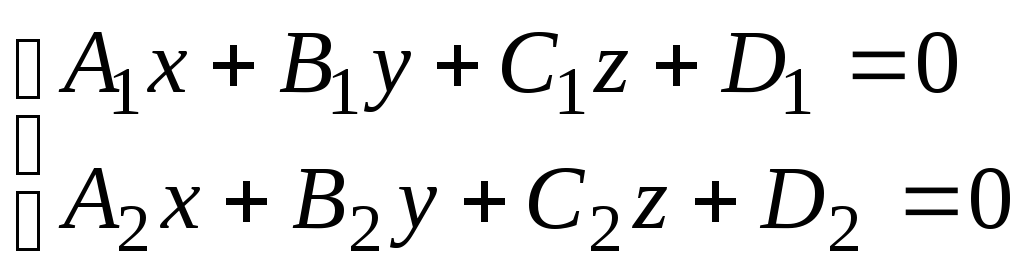где коэффициенты при неизвестных непропорциональны, – координатная форма записи.

Вывод: для того чтобы составить уравнения прямой в пространстве следует знать ее направляющий вектор и какую-либо точку. Кроме того, прямую в пространстве можно задать пересечением двух непараллельных плоскостей.