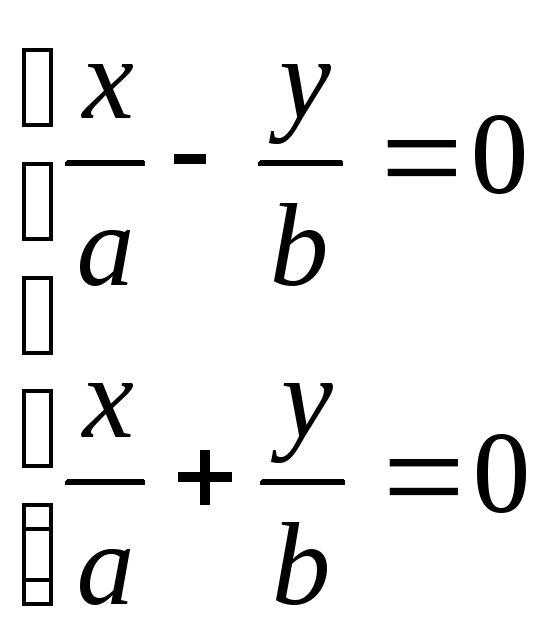- •Глава 3. Линии второго порядка § 1. Гипербола
- •Вывод канонического уравнения
- •Исследование формы гиперболы по ее каноническому уравнению
- •§ 2. Эллипс
- •Вывод канонического уравнения
- •Исследование формы эллипса по его каноническому уравнению
- •Параметрические уравнения эллипса
- •§ 3. Парабола
- •Вывод канонического уравнения
- •§ 4. Эксцентриситет и директрисы эллипса и гиперболы
- •§ 5. Полярные уравнения эллипса, гиперболы и параболы Полярная система координат
- •Вывод полярных уравнений
- •§ 6. Касательные к эллипсу, гиперболе, параболе
- •§ 7. Оптические свойства эллипса, гиперболы и параболы
- •§ 8. Линии второго порядка
§ 7. Оптические свойства эллипса, гиперболы и параболы
Теорема. Лучи света, выходящий из одного фокуса эллипса, после отражения от эллипса проходят через другой его фокус (рис. 3.16).
Л
Рис. 1.
Рис. 2.
Л учи
света, выходящие из одного фокуса
гиперболы, после отражения от гиперболы
кажутся выходящими из другого её фокуса
(рис. 3.18).
учи
света, выходящие из одного фокуса
гиперболы, после отражения от гиперболы
кажутся выходящими из другого её фокуса
(рис. 3.18).
►Для гиперболы.
Покажем, что нормаль
![]() к гиперболе в ее точке
к гиперболе в ее точке
![]() образует одинаковые углы с лучом,
выходящим из правого фокуса, и с лучом,
кажущимся выходящим из левого фокуса.
Обозначим
образует одинаковые углы с лучом,
выходящим из правого фокуса, и с лучом,
кажущимся выходящим из левого фокуса.
Обозначим
![]() (рис. 3.17). Согласно (4) § 6
(рис. 3.17). Согласно (4) § 6
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() ,
,
![]() .Тогда:
.Тогда:
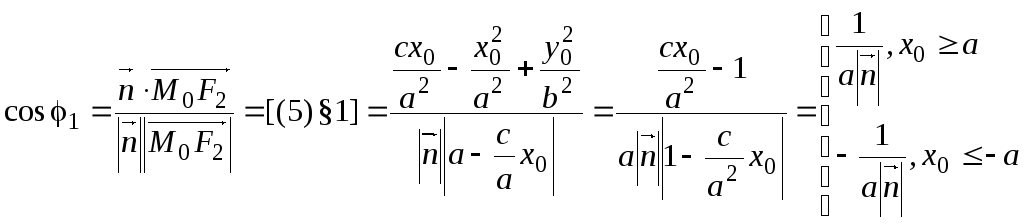 ,
(1)
,
(1)
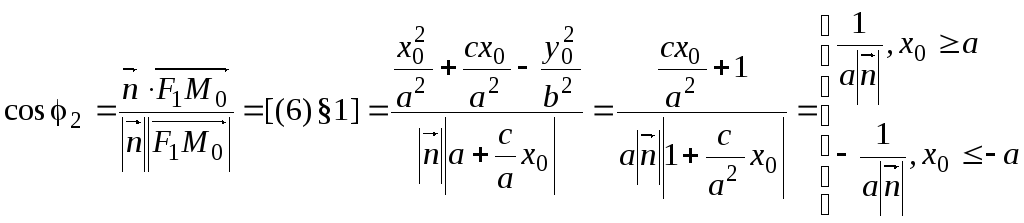 .
(2)
.
(2)
С равнивая
(1) и (2) и учитывая, что оба угла
равнивая
(1) и (2) и учитывая, что оба угла
![]() и
и
![]() находятся в пределах от 0 до
находятся в пределах от 0 до
![]() ,
получаем, что
,
получаем, что
![]() =
=
![]() .
.
Для параболы.
Обозначим
![]() ,
,
![]() (рис. 3.18). На основании (6) § 6
(рис. 3.18). На основании (6) § 6
![]() .
Тогда
.
Тогда
![]() и
и
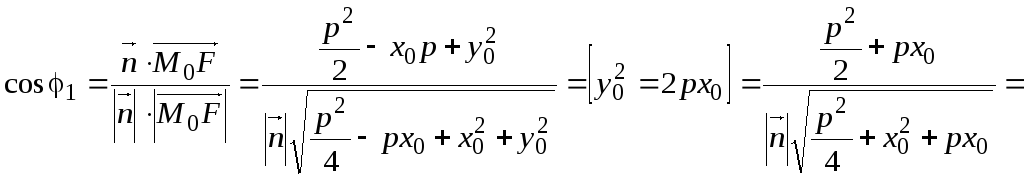
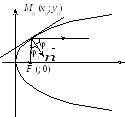
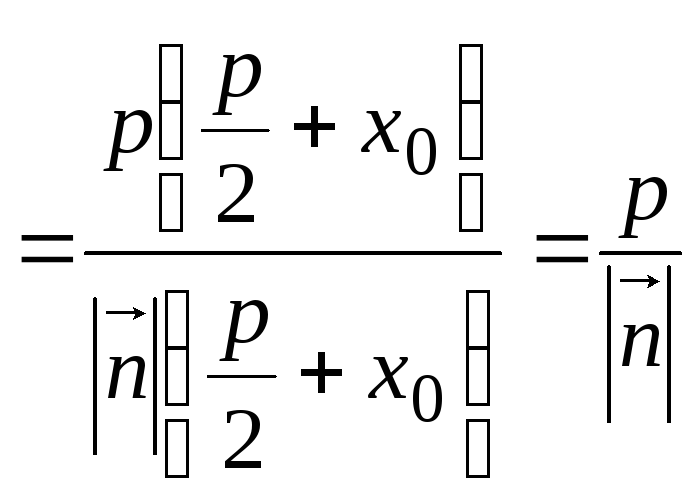 ,
(5)
,
(5)
![]() .
(6)
.
(6)
Сравнивая (5) и (6),
опять же получаем, что
![]() .
.
Для эллипса оптическое свойство до- Рис. 3.18 казывается точно так же, как и для гиперболы, поэтому вы можете сделать это самостоятельно в качестве упражнения. ◄
Рис.5.
§ 8. Линии второго порядка
Будем считать, что на плоскости задана прямоугольная декартова система координат.
Уравнением второй степени с двумя неизвестными называется уравнение вида
![]() ,
,
в котором
![]() .
.
Уравнение второй степени называется каноническим, если оно удовлетворяет следующим условиям:
-
не содержит произведения переменных (
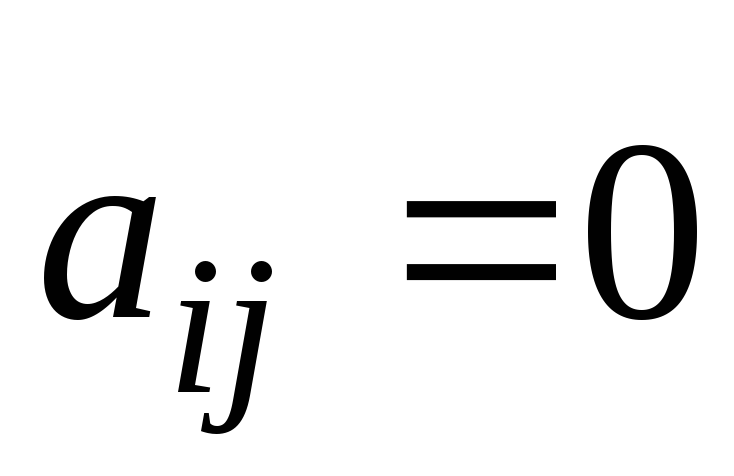 при
при
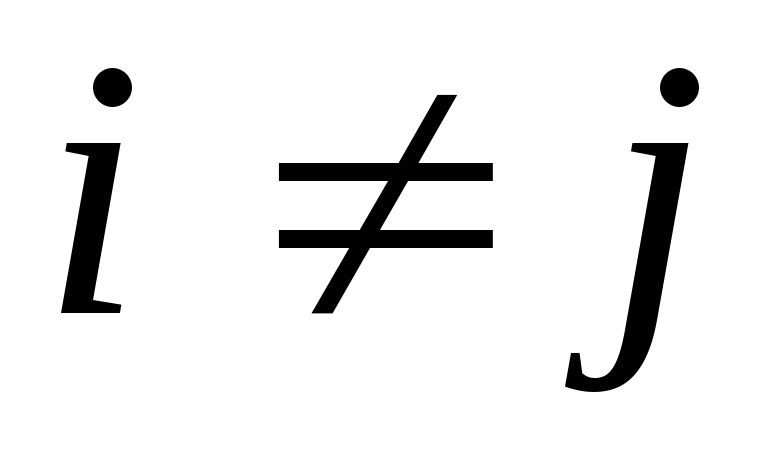 );
); -
если содержит квадрат какой-либо переменной, то не содержит её первой степени (
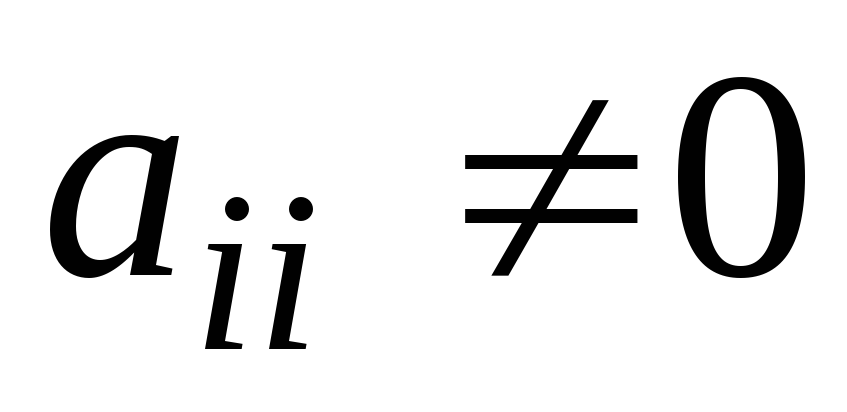 =>
=>
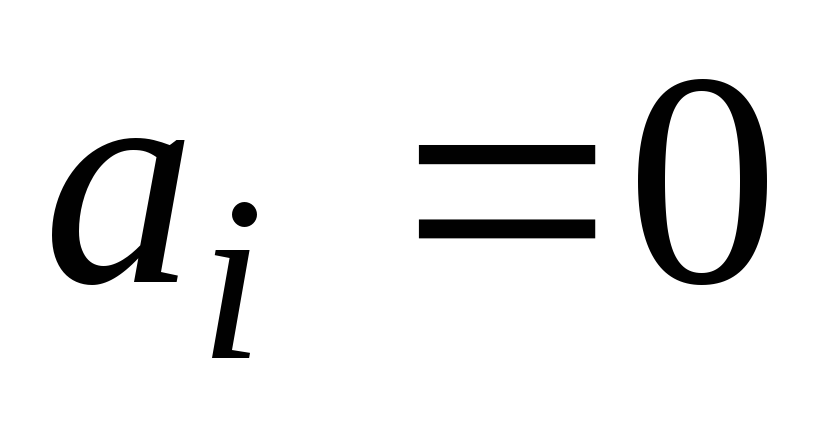 );
); -
если содержит первую степень, то только одной переменной, и тогда свободный член равен нулю (
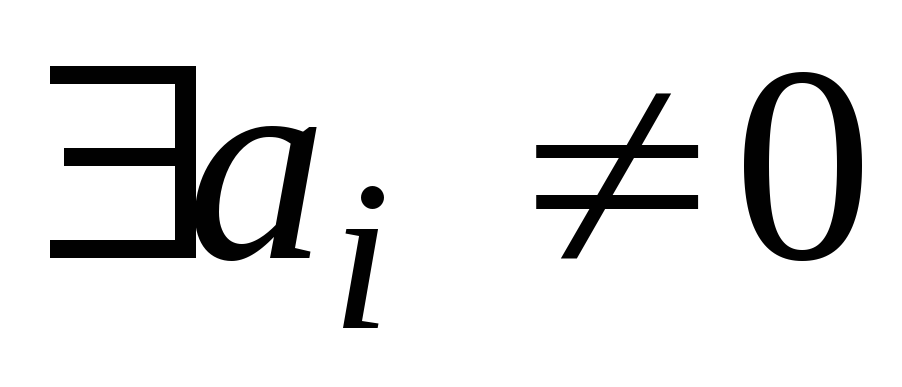 =>
=>
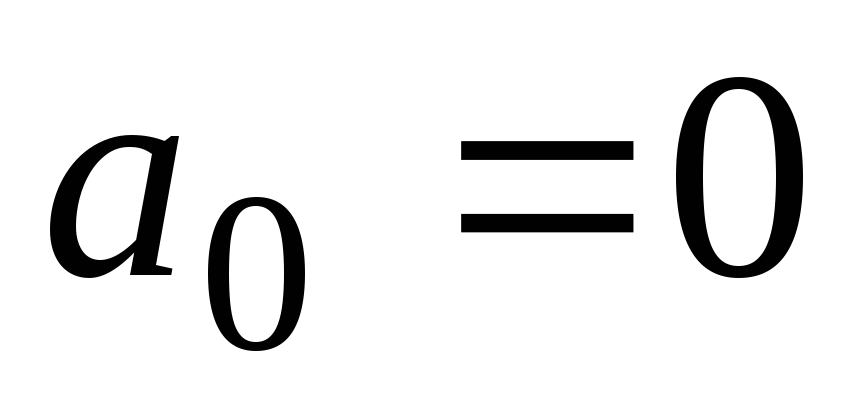 );
); -
если свободный член не равен нулю, то он равен 1 или -1.
Линией второго порядка называется множество точек плоскости, удовлетворяющих какому-либо уравнению 2-й степени.
Теорема. Для любой линии второго 2-го порядка на плоскости существует прямоугольная декартова система координат, в которой эта линия задаётся каноническим уравнением.
Эту теорему мы докажем позже, в разделе «Линейная алгебра», а сейчас на основании ее мы перечислим все возможные типы линий второго порядка:
|
|
эллипс; |
|
|
мнимый эллипс; |
|
|
точка О(0; 0); |
|
|
гипербола; |
|
|
пара пересекающихся прямых; |
|
|
парабола; |
|
|
пара параллельных прямых; |
|
|
сдвоенная прямая; |
|
|
пара мнимых параллельных прямых. |