Параметрические уравнения эллипса

П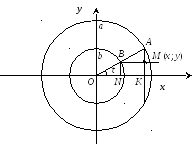усть задан эллипс своим каноническим уравнением (4), где . Построим две окружности радиусами и соответственно с центрами в начале координат. Из начала координат проведем луч под углом к положительному направлению оси , и обозначим А и В точки его пересечения соответственно с большей и меньшей окружностями. Че-

Рис. 3.6. рез точку А проведём вертикальную прямую, через В – горизонтальную, их пересечение обозначим М. Кроме того, обозначим K и N основания перпендикуляров, опущенных на ось соответственно из точек А и В (рис.3.6).

Если точка M имеет координаты (x; y), то по рис. 3.6 видно, что

,.

Координаты точки M удовлетворяют (4), значит, M принадлежит эллипсу. Очевидно, если изменяется в пределах от 0 до 2, то мы получим все точки эллипса. Отсюда вытекает один из способов построения точек эллипса. Кроме того, мы вывели его параметрические уравнения:

.

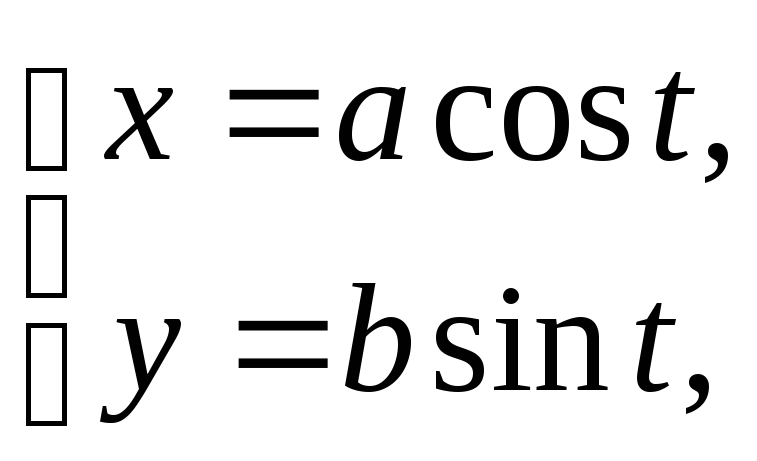
§ 3. Парабола

Определение. Пусть на плоскости заданы прямая  и точка F на расстоянии p от неё. Параболой называется множество всех точек той же плоскости, для каждой из которых расстояние до точки F, называемой фокусом параболы, равно расстоянию до прямой , называемой ее директрисой.

Вывод канонического уравнения

В

ыберем на плоскости прямоугольную декартову систему координат следующим образом: ось направим через фокус параболы перпендикулярно директрисе в направлении от неё, ось проведем посредине между фокусом и директрисой параллельно последней. Если – произвольная точка параболы, то определение

Рис.3.7 параболы формально запишется в виде равенства ,или

. (1)

С учётом того, что в выбранной системе координат , , , получаем:

(1)

Рис. 2.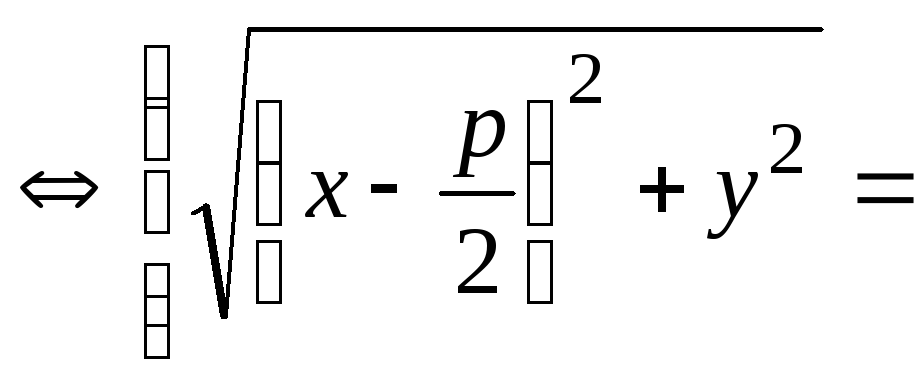

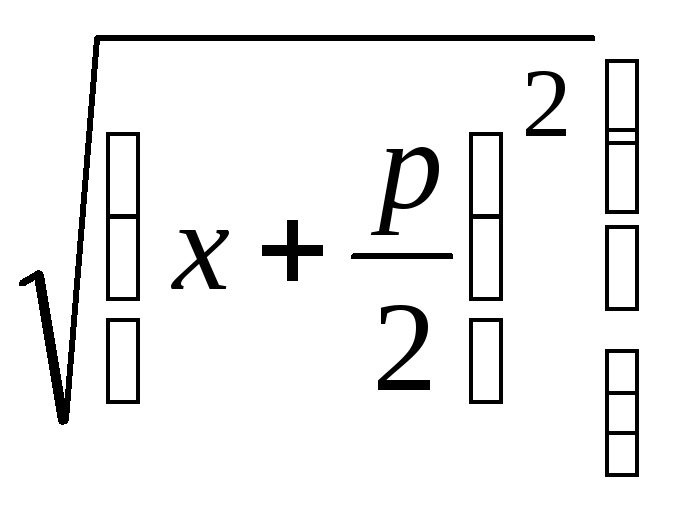
. Отсюда и вытекает уравнение параболы

, (2)

н

Рис.3.8

азываемое каноническим. Число p в этом уравнении (расстояние от фокуса до директрисы) носит название фокального параметра. Парабола с уравнением (2) отличается от школьной только тем, что в ней переменные и поменялись ролями. Поэтому мы не будем подробно останавливаться на исследовании её формы, а как она выглядит, посмотрите на рис. 3.8.

§ 4. Эксцентриситет и директрисы эллипса и гиперболы

Эксцентриситетом гиперболы называется число , равное отношению половины расстояния между фокусами гиперболы к ее действительной полуоси.

Эксцентриситетом эллипса называется число , равное отношению половины расстояния между фокусами эллипса к его большой полуоси.

Директрисами гиперболы называются прямые, перпендикулярные ее действительной оси и находящиеся от центра на расстоянии, равном отношению действительной полуоси к эксцентриситету.

Директрисами эллипса называются прямые, перпендикулярные его большой оси и находящиеся от центра на расстоянии, равном отношению большой полуоси к эксцентриситету.

, (1)	, (1I)
, a > b (2)	, a < b, (2I)
,	,
уравнения директрис: .	уравнения директрис: .

Р

.

Рис. 1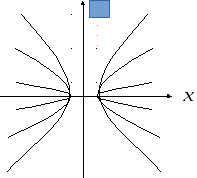

ассмотрим гиперболу (1). Для неё , т.к. . Вспомнив, что , получаем . Исследуем, как меняется форма гиперболы в зависимости от её эксцентриситета. Зафиксируем полуось . Если , то , т.е. гипербола будет очень узкой. С ростом растёт и , т.е. ветви гиперболы расширяются (см. рис. 3.9). Если же , то и , т.е. гипербола по внешнему виду приближается к паре параллельных прямых.

Рассмотрим теперь эллипс (2). Для него , т.к. . Для эллипса (2)

Рис.3.9 , поэтому . Исследуем, как меняется форма эллипса в зависимости от его эксцентриситета. Опять зафиксируем полуось . При получаем , и эллипс вырождается в окружность. С ростом полуось уменьшается, эллипс «худеет», а если , то , т.е. эллипс и вовсе стремится превратиться в отрезок (рис 3.10).

Теперь вернемся к директрисам. Так как для гиперболы (1) , а для эллипса (2) , Рис. 3.10

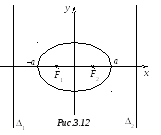
то для гиперболы , а для эллипса . Это значит, что и директрисы гиперболы, и директрисы эллипса свою кривую не пересекают. Кроме того, директриса и соответствующий ей фокус отделены кривой друг от друга (рис. 3.11 и 3.12).

Теорема (основное свойство эллипса и гиперболы по отношению к директрисам). Для всех точек гиперболы (эллипса) отношение расстояния до фокуса к расстоянию до соответствующей этому фокусу директрисы есть число постоянное, равное эксцентриситету гиперболы (эллипса). И обратно: если для какой-либо точки плоскости отношение расстояния до фокуса заданной гиперболы (эллипса) к расстоянию до соответствующей этому фокусу директрисы равно эксцентриситету заданной гиперболы (эллипса), то эта точка принадлежит гиперболе (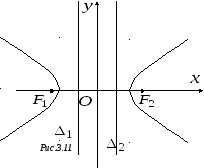 эллипсу).

►Докажем утверждение для левого фокуса и левой директрисы гиперболы (1) (в остальных случаях вы его докажете самостоятельно в качестве упражнения). На рис. 3.13 точки имеют следующие координаты: ,, . Тогда

[§1, (5)] = ; .

И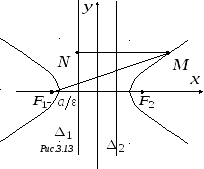 з этих двух равенств и получаем:

.

Докажем обратное утверждение. Пусть для некоторой точки плоскости справедливо соотношение:

. (3)

Так как , а , то

(3)

.

Учитывая, что , из последнего уравнения получаем . Таким образом, точка удовлетворяет уравнению заданной гиперболы. ◄

На основании доказанной теоремы мы можем сформулировать общее определение эллипса, гиперболы и параболы.

Определение. Гиперболой (эллипсом, параболой) называется множество точек плоскости, для каждой из которых отношение расстояния до заданной точки к расстоянию до заданной прямой в этой плоскости есть число постоянное, равное , причём  > 1 ( < 1,  = 1).