9. Базы знаний и их применение для формирования экономических решений

Базу знаний, как одну из форм информационной модели, следует рассмотреть отдельно из-за ее исключительной перспективности в формировании решений. Будучи предметом изучения специального научного направления, известного под названием инженерия знаний, базы знаний легли в основу создания экспертных систем, одного из продуктов искусственного интеллекта. База знаний – это одна из форм информационного моделирования, представляющая собой знания человека (эксперта, специалиста), помещенные в память компьютера в соответствии с некоторой моделью. Модель, как известно, - это правила или соглашения, выполнение которых позволяет представить некоторую сферу знаний в том виде, которая позволяет использовать формальные (программные) средства для их обработки (получение новых знаний).

Существует множество моделей представления знаний. Для рассмотрения выделим следующие:

-семантические сети;

-деревья выводов;

- деревья целей;

- нечеткие множества.

Семантическая сеть – это ориентированный граф, вершины (узлы) которого соответствуют понятиям моделируемой предметной области, а дуги – отношениям между ними. В качестве понятий обычно выступают конкретные или абстрактные объекты, а отношений – связи. В отличие от всех других моделей базы знаний могут содержать описание связей в явной форме, указанных с помощью синтаксических, семантических и прагматических отношений. Наиболее часто в семантических сетях используется следующие отношения:

-целое-часть (класс – подкласс, элемент – множество и т.д.);

-функциональная связь, определяемая глаголом (производит, находится, поставляет … и т.д.);

-атрибутивные (иметь значение, иметь свойство);

- логические (И, ИЛИ, НЕТ);

- временные (в течение, раньше, позже…).

Пояснить базу знаний легче в сравнении с базой данных, так как различия между ними нечеткие (размытые). Обратимся к рис. 5.21, на котором представлена информация о поставках, поставщиках и прочее с помощью реляционной базы данных и базы знаний в виде семантической сети.

Анализируя базу данных и базу знаний можно заметить, что в базе данных информация более скудная и поэтому с уверенностью трудно ответить на вопрос: Арматура это товар, который производит производитель или это то, что поставляет поставщик? В то же время семантическая сеть прямо указывает на то, что арматура – это товар, который поставляет ООО “Восход”, а производит ее ООО” Рассвет”. Также можно определить поставщика и производителя строительных блоков: блоки поставляет ООО “Юг”, а производит их ООО “Север”. Кроме того, указано, что ООО “Восход” относится к поставщикам, а ООО “Рассвет” к производителям, ООО “Север” находится в Северо-Западном округе.

Таким образом, отличие баз знаний от баз данных состоит в том, что первые содержат связи между объектами в явной форме, тогда как у вторых эти связи скрыты.

Обрабатывается семантическая сеть на основе принципа сопоставления объекта и отношений, указанных в запросе, с объектами и отношениями, имеющимися в семантической сети. Например, если запрос имеет вид "Что производит ООО "Рассвет"? будет выделен тот фрагмент сети, где фигурирует указанный объект ("Рассвет") и отношение "производит". Ответом будет: "ООО "Рассвет" производит арматуру".

С помощью приведенной на рис. 5.29 семантической сети можно получить, кроме прочих, ответы на следующие вопросы:

1. Какие предприятия производят арматуру?

2. Какие предприятия поставляют арматуру?

3. В каком регионе находятся ООО “Север”?

4. Является ли поставщиком ООО “Восход”? и т.д.

Дерево вывода – это множество объединенных правил, отражающих условия выполнения некоторого процесса. Правила представляют собой языковую конструкцию вида:

ЕСЛИ <условие, ct(условия)>, ТО <заключение, ct(заключения)> ct(правила),

где ct(условия) – коэффициент определенности условия;

ct(заключения) - коэффициент определенности заключения;

ct(правила) - коэффициент определенности правила.

Коэффициент, равный 0, указывает на полную неопределенность, а 1 – на полную определенность. В правиле эксперт указывает значения в этом диапазоне.

Множество правил объединяются в дерево вывода. Рассмотрим пример.

Пусть задано два правила.

Правило 1. ЕСЛИ индекс цен возрастет не менее чем на 3% (условие В)

ct(В)

И цены на энергоносители вырастут не более чем на 19%

(условие С), ct(С) = 0,6

ТО акции покупать (заключение А) ct(А) =?, ct(правила 1) =

0,8.

Правило 2. ЕСЛИ ВВП возрастет не менее чем на 1,5% (условие Д) ct(Д)

= 0,4

ИЛИ ставки Центрального банка будут в пределах 12%

(условие Е) ct(Е) = 0,7

ИЛИ объем экспорта возрастет более чем на 5% (условие G)

ct(G) = 0,5

ТО индекс цен возрастет не менее чем на 3%. (заключение В)

ct(В) = ?, ct(правила 2) = 0,98.

Эти правила объединяются в дерево, представленное на рис. 5.30.

Рассмотрим, каким образом знания такого рода представляются графически, а также как рассчитывается коэффициент определенности заключения. Правило с одним условием вида ЕСЛИ А, ТО В графически представится следующим образом:

Здесь А - это условие, В - заключение. Далее условимся заключение, получаемое с помощью правила, изображать сверху, а условия - снизу. Число рядом с условием указывает на его определенность, а число рядом с линией - на определенность самого правила.

Условий в правиле может быть несколько, которые связанны между собой союзами И или ИЛИ. Например

ЕСЛИ А и В и С, ТО Е,

ЕСЛИ А или В или С, ТО Е.

Графически эти правила изображаются так, как это показано на рис. 5.31.

Сплошная или пунктирная дуга указывает на вид объединения условий: союзом И или союзом ИЛИ соответственно. Число, находящееся рядом с дугой (сплошной или пунктирной), указывает на определенность правила, а число рядом с условиями и заключениями - на определенность условий и заключений. Лицо, принимающее решение, условиям (А, В, С), а также правилу присваивает коэффициент определенности от 0 до 1. С помощью специальных формул рассчитывается коэффициент определенности для заключения.

Для простого правила, содержащего лишь одно условие, например, ЕСЛИ Е, ТО С, коэффициент определенности для заключения С рассчитывается так:

ct(C) = ct(E) · ct(правила)

где ct(C) - коэффициент определенности заключения С;

ct(E) - коэффициент определенности условия Е;

сt(правила) - коэффициент определенности правила.

Пример: при ct(E) = 0,4;

ct(правила) = 0,2;

коэффициент определенности заключения равен ct(C)=0,08.

Если в правиле несколько условий, связанных союзом И, то для расчета коэффициента определенности заключения применяется следующая операция:

ЕСЛИ(Е1 и Е2), ТО С.

сt(С) = min(ct(E1), ct(E2)) * сt(правила) .

Для правила, в котором присутствуют несколько условий, связанных связкой ИЛИ, применяется операция вида:

ЕСЛИ (Е1 или Е2), ТО С.

ct(С) = max(ct(E1), ct(E2)) * сt(правила).

Пример:

ЕСЛИ (Е1 и Е2),ТО С. При ct(E1)=0,7; ct(E2)=0,6; ct(правила)=0,8;

ct(условия) = min(0,7;0,6)=0,6 коэффициент определенности заключения равен ct(С)=0,6 · 0,8=0,48.

Для заключения А, вывод которого представлен на рис. 5.13, при ct(Д) = 0,8; ct(Е) = 0,5; ct(G) = 0,6; ct(пр1) = 0,7; ct(С) = 0,4; ct(пр2) = 0,3, его коэффициент определенности равен ct(А) = 0,12.

Дерево целей является дальнейшим совершенствованием целевого управления, развиваемым в нашей стране с семидесятых годов прошлого столетия. В основу его построения положено понятие цели, измерение достижения которой осуществляется с помощью значений соответствующих экономических показателей. Например, уровень достижения цели “Увеличить рентабельность предприятия” можно измерить показателем “Рентабельность” в числовом диапазоне от 0 до 1. Цель “Увеличить рентабельность предприятия с 0,3 до 0,5” в дереве целей указывается именно таким образом.

Допустим, целью является увеличение прибыли, которое обычно достигается за счет увеличения выручки и снижения затрат. Это можно представить графически. Для примера на рис. 5.32 представлена часть дерева целей, на котором с помощью знаков плюс и минус показаны желаемые направления изменения подцелей: В (выручка) - увеличение, З (затраты) - снижение, П (прибыль) - увеличение. Если В = 20 ед., З = 15 ед, то П = 5 ед.

Используется дерево целей для формирования решений следующим образом: допустим, необходимо поднять прибыль до 7 ед. Для этого необходимо установить приоритеты путей в достижении данной цели с помощью коэффициентов α и β. Пользуясь типовыми формулами обратных вычислений, можно определить каковыми должны быть выручка и затраты:

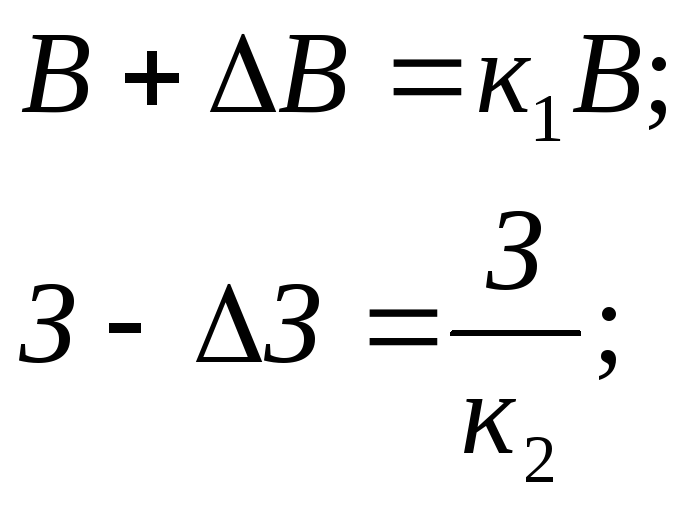
где и - искомый прирост выручки, и искомое снижение затрат.

Подставив исходные данные, при и ,получим:

= 1,07; = 1,04; = 21,4; = 14,4. Сделаем проверку правильности полученных результатов: = 21,4 – 14,4 = 7.

Дерево целей можно продолжить, если указать из чего состоят выручка и затраты. Это позволит рассчитать управляющие воздействия более детального характера (см. раздел 8.4). Представление знаний в виде дерева целей возможно, если известна цель управления и формулы, согласно которым можно рассчитать уровень достижения каждой из подцелей.

В процессе создания моделей баз знаний специалисты сталкиваются с проблемой отражения и использования нечеткой, то есть неопределенной информации. Представление таких знаний “как высокий человек”, “добросовестный поставщик”, “надежный партнер” и т.д., потребовали нового взгляда на методы их формализации. Задачи, решаемые человеком, в большинстве случаев опираются именно на нечеткие, размытые и неопределенные знания о процессах или событиях.

Нечеткие множества.

Знания человека в большинстве случаев нечеткие. Человек оперирует такими понятиями как высокий, низкий, горячее, холодное, бедный, богатый и т.д. в повседневной производственной практике и в быту. Для того чтобы такого рода знания можно было использовать для формирования решений, в 1965 году Л.Заде предложил теорию нечетких множеств. В основе данной теории лежит понятие функции принадлежности, которая указывает степень принадлежности какого-либо элемента некоторому множеству элементов. Данная функция является субъективной и строится на основании знаний, опыта или ощущений некоторого субъекта к какому-либо объекту, процессу, явлению и т.д.

Вводится U – полное множество, охватывающее все объекты некоторого класса. Нечеткое подмножество F множества U определяется через функцию принадлежности , где . Эта функция отображает элементы u множества U на множество чисел в отрезке [0,1], которые указывают степень принадлежности этих элементов множеству F.

Нечеткое множество F можно представить следующим образом:

Знак + указывает не на сложение, а на совокупность, а знак / - не деления, а на степень принадлежности.

Рассмотрим пример. Пусть имеется два множества:

и .

Степень принадлежности элементов множества Е множеству А можно однозначно представить как: , , , , . На рис. 5.33 иллюстрируется четкая (однозначная) принадлежность элементов одного множества другому.

Но принадлежность элементов может характеризоваться и приблизительно, например:

• более или менее принадлежит;

• скорее принадлежит;

• возможно принадлежит и т.д.

Для этого можно воспользоваться функцией принадлежности, которая записывается в данном случае следующим образом:

Если функцию принадлежности применить для четких множеств (см. рис. 5.33), то можно получить следующее:

Как правило, функции принадлежности иллюстрируются графически. На рис. 5.34 представлено субъективное понимание возраста с помощью функций принадлежности и графиков.

На рис. 5.35 представлено субъективное понимание понятия «низкие процентные ставки».

Для того чтобы функцию принадлежности можно было использовать в практических расчетах, вводятся операции пересечения и объединения нечетких множеств.

Операция пересечения нечетких множеств соответствует нахождению минимума значений их функций принадлежности:

, , .

Операция объединения соответствует максимуму значений их функций принадлежности, то есть:

.